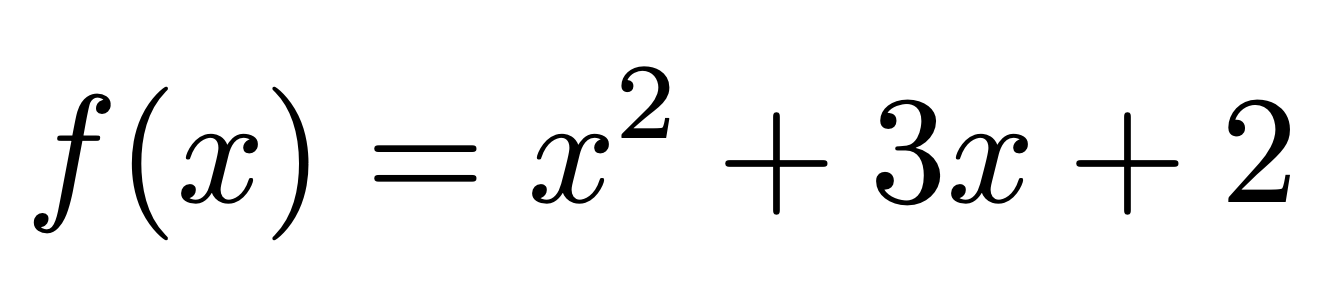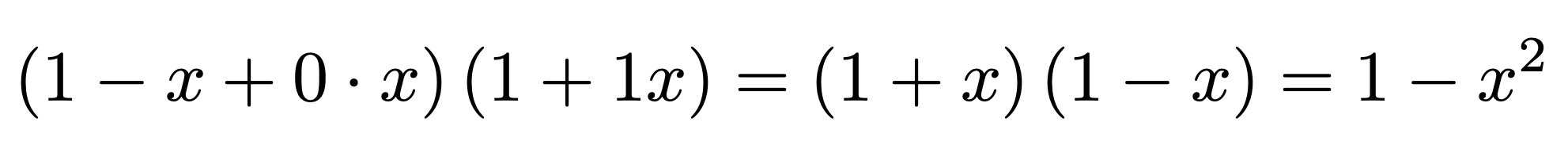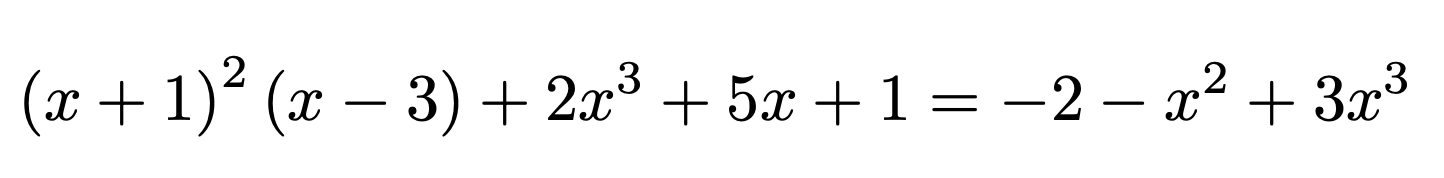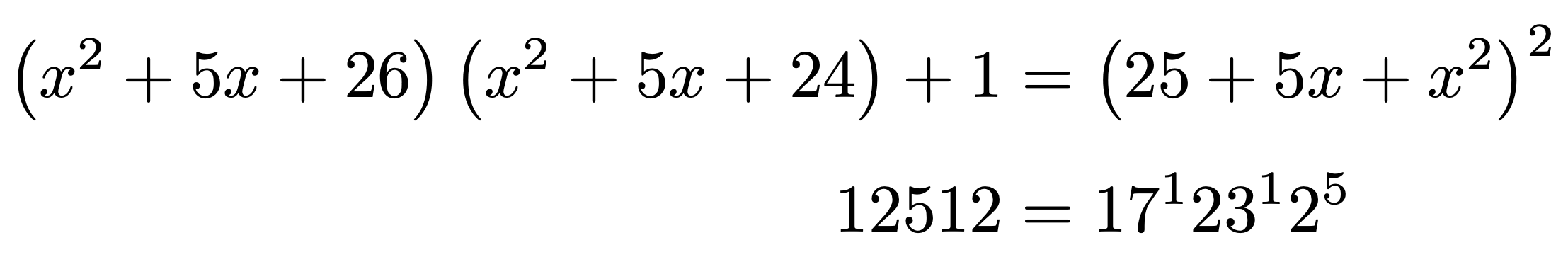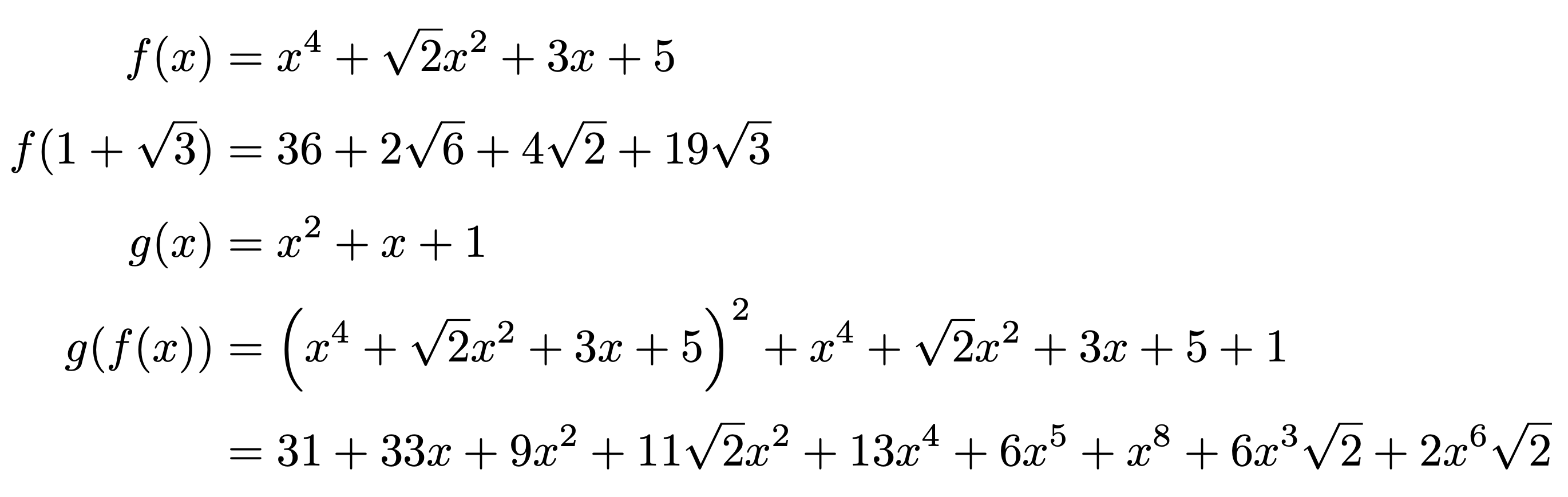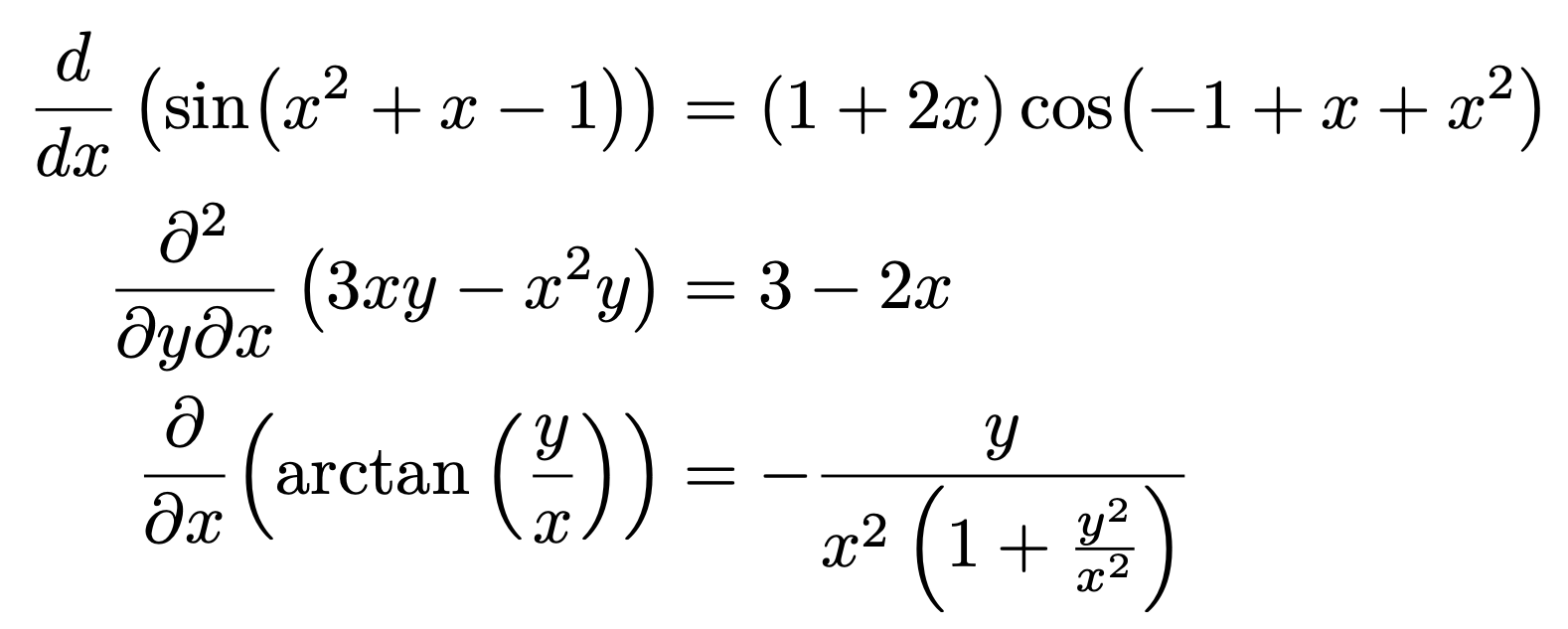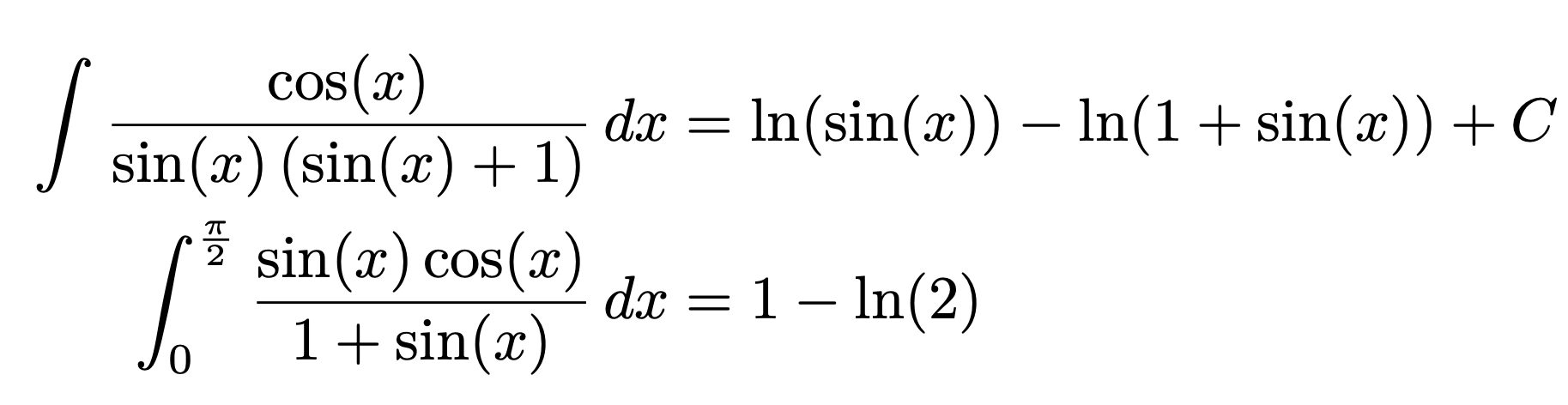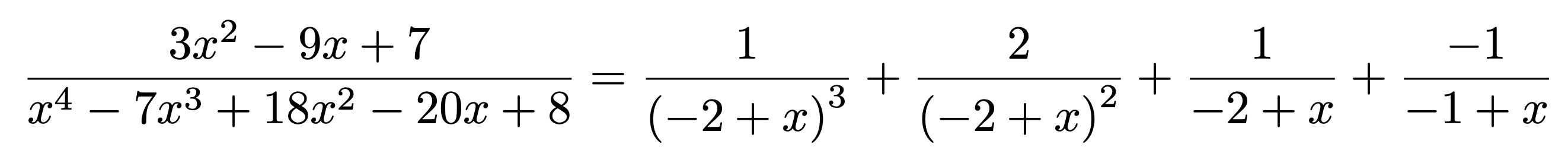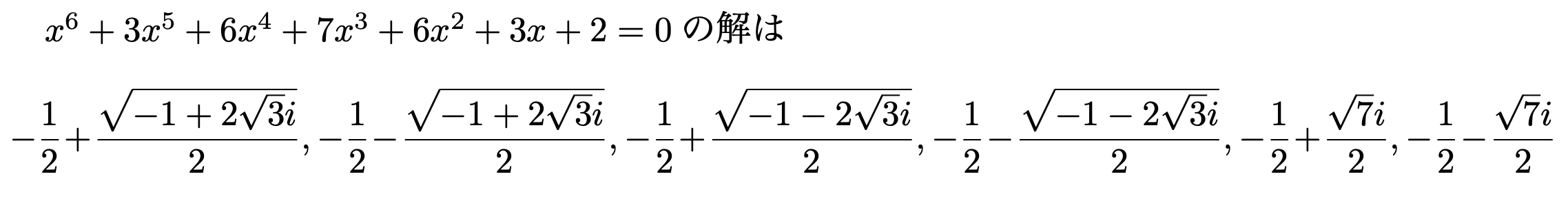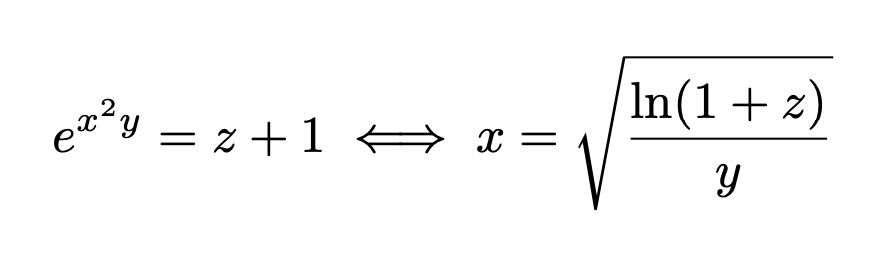luacasパッケージを使ってLaTeX文書内で数式処理をする

0. はじめに

この記事は物工/計数 Advent Calender 2022の17日目の記事です。
この記事のテーマは、先日2022/11/06にCTAN(Comprehensive TeX Archive Network)に追加されたばかりのLaTeXパッケージであるluacasパッケージについてです。
luacasパッケージは、簡単にいうとLaTeX文書内で数式処理をするためのパッケージです(CAS: Computer Algebra System)。例えば微積分なんかをやってくれます。
luacasの公式ドキュメントにおいては次のように書かれています。

The package luacas allows for symbolic computation within LaTeX.

1. luacasを使うための準備

luacasの使用例を早く見たい人はここは飛ばして2. 使ってみるを見てください

luacasパッケージは

• LuaLaTeXでのみ利用できる（pLaTeXやupLaTeXでは利用できない)
  • 自分がどのエンジンでLaTeXを使っているのかわからないという方もしれませんが、少なくともjsarticleなどを使っていればまあ(u)pLaTeXだと思います。
• ごく最近発表されたパッケージである

という2点から、使うまでに少し準備が必要です。
人によってはこの準備にちょっと時間かかるかもしれません。

LuaLaTeXでのビルド環境を整える

自分なりの設定をしたい人は勝手に自分でやってください。以下はVSCodeでLaTeX Workshopを使ってる人向けの説明です。
ここではcluttexというLaTeX処理の自動化ツールを使って環境構築します(楽なので)。

1. settings.jsonを開く

2. "latex-workshop.latex.tools"に以下を追加

   追記内容

   biberじゃなくてbibtexが良い人とかはcluttexの仕様見ながらよしなに書き換えてください

   settings.json

   {
     "name": "cluttex",
     "command": "cluttex",
     "args": [
       "--engine=lualatex",
       "--makeindex=upmendex",
       "--biber=biber",
       "-synctex=1",
       "-shell-escape",
       "%DOC%"
     ],
   }
   

3. "latex-workshop.latex.recipes"の一番上に以下を追加(一番上に追加したレシピがデフォルトのビルドレシピとなります）

   追記内容

   settings.json

   {
     "name": "cluttex",
     "tools": [
       "cluttex",
     ]
   }
   

4. プリアンプルなどをよしなに書き換える
   LuaLaTeXにおいてはjsarticleとかが使えなくなるので、よしなに書き換えます。

   ちなみに僕がよく使うプリアンプルはこんな感じです

   LuaLaTeXは(u)pLaTeXと違い、PDFを生成する際にdviファイルを経由しないため、graphicxなどのインポートの際にdvipdfmxなどのドライバを指定する必要がなくなります。

   \documentclass{jlreq}
   
   \usepackage{amsmath,amssymb}
   \usepackage{physics}
   \usepackage{graphicx}
   \usepackage{float}
   \usepackage{enumitem}
   
   \usepackage[no-math]{luatexja-fontspec}
   \setmainfont[Ligatures=TeX]{TeXGyreTermes}
   \setsansfont[Ligatures=TeX]{TeXGyreHeros}
   \setmainjfont[BoldFont=HiraMinProN-W6]{HiraMinProN-W3}
   \setsansjfont[BoldFont=HiraKakuProN-W6]{HiraKakuProN-W3}
   
   
   \begin{document}
   

(TeX Liveを使っている人向け)TeX Liveをupdateし、luacasを入手

ターミナルで

shell

> sudo tlmgr update --self --all

を実行することでTeX Liveをupdateできます。久々にupdateする場合だと結構時間かかると思います。

shell

> kpsewhich luacas.sty
/usr/local/texlive/2022/texmf-dist/tex/lualatex/luacas/luacas.sty

こんな感じでluacas.styが見つかってくれればOKです。
overleafとか使ってる方はluacasパッケージのページからstyファイルを入手すればいいんじゃないですかね。

2. 使ってみる

\usepackage{luacas}をプリアンプルに追加して始めましょう。

sampleのgitリポジトリ

以下で説明している内容はこのリポジトリ内のtexファイルに書いてあります。参考程度に手元でも動かしてみてください。

使い方

\begin{CAS}...\end{CAS}の中に記述し、　\print{}によって出力します。
\begin{CAS}...\end{CAS}の中での定義は文書内でグローバルなもののようです。

\begin{CAS}
    vars('x')
    f = x^2 + 3*x + 2
\end{CAS}
\[ f(x)=\print{f} \]

出力

基本の関数

計算結果を簡単にする： f:autosimplify() \print*{} f:simplify()

luacas_example.tex

\begin{CAS}
	vars('x')
	f = (1 - x + 0*x)*(1 + 1*x)
\end{CAS}
\[　\print{f}=\print{f:autosimplify()} = \print{f:simplify()}　\]

出力

• \print*{f}は\print{f:autosimplify()}と等価です。ですので簡単な\print*{f}の方をメインで使うようになるのではないかと思います。
• f:autosimplify()とf:simplify()は別のコマンドです。f:simplify()は出てくる項の数を極力少なくするように変形するらしく、こちらの方がやや強いコマンドなのではないかと思います（詳細はよくわからない）。
• 降べきの順になってほしいけど、デフォルトでは昇べきの順になるようです。簡単に変更する方法あるんですかね。

展開する： f:expand()

luacas_example.tex

\begin{CAS}
    vars('x')
	f = (x + 1)^2*(x - 3) + (2*x^3 + 5*x + 1)
\end{CAS}
\[ \print{f}=\print{f:expand()} \]

出力

因数分解(or素因数分解)する： factor(f)

luacas_example.tex

\begin{CAS}
    vars('x')
	f = (x^2 + 5*x + 26)*(x^2 + 5*x + 24) + 1
	a = 12512
\end{CAS}
\begin{align*}
	\print{f} & =\print{factor(f:expand())} \\
	\print{a} & =\print{factor(a)}
\end{align*}

出力

• 整式に対して適用すると因数分解され、整数に対して適用すると素因数分解されるようです。
• aのように変数に数値を代入する場合は色々気をつけることがある的なことが公式ドキュメントに書いてあったのですが、よくわからなかったので気になる方は公式ドキュメントを読んでください。

代入する： substitute({[x]=a},f)

luacas_example.tex

\begin{CAS}
    vars('x')
	f = x^4 + sqrt(2)*x^2 + 3*x + 5
	subs = {[x]=1+sqrt(3)}
	g = x^2 + x + 1
\end{CAS}
\begin{align*}
	f(x)          & =\print{f}                               \\
	f(1+\sqrt{3}) & =\print*{substitute(subs,f):simplify()}  \\
	g(x)          & =\print{g}                               \\
	g(f(x))       & =\print{substitute({[x]=f},g)}           \\
	              & =\print*{substitute({[x]=f},g):expand()}
\end{align*}

出力

• {[x]=hoge}みたいな代入内容を\begin{CAS}...\end{CAS}の中に書くか\print{}の中に書くかで微妙に挙動が違うことがあるのが気になります（詳細はよくわかっていないが、おそらく前述のようにluacasの数値の扱いにちょっとクセがあることが影響しているのではないかと思う）。
• 数値だけでなく文字を代入することもできます(g(f(x))参照)。

さまざまな演算

微分する： diff(f,x)

luacas_example.tex

\begin{CAS}
	vars('x','y')
	f = sin(x^2+x-1)
	fx = diff(f, x)
	g = 3*x*y - x^2*y
	gxy = diff(g, x, y)
	h = arctan(y/x)
\end{CAS}
\begin{align*}
	\print{fx}                              & =\print*{fx}        \\
	\print{gxy}                             & =\print*{gxy}       \\
	\pdv{}{x}\qty(\arctan\qty(\frac{y}{x})) & =\print*{diff(h,x)}
\end{align*}

出力

• gやhのような2変数関数に対しても使えます。diff(g,x,y)とすると$\frac{\partial^2g}{\partial y\partial x}$となります。
• 2変数関数に対し1つの変数で微分すると偏微分を計算しますが、そのままprintしたときの微分記号は$\frac{\partial}{\partial x}$ではなく$\frac{d}{dx}$でした。
• \qtyや\pdvはphysicsパッケージのコマンドです。

積分する： int(f,x,a,b)

luacas_example.tex

\begin{CAS}
    vars('x')
	f = cos(x)/(sin(x)*(sin(x)+1))
	intf = int(f, x)
	g = sin(x)*cos(x)/(1+sin(x))
	intg = int(g, x, 0, pi/2)
\end{CAS}
\begin{align*}
	\print{intf} & =\print*{intf}+C \\
	\print{intg} & =\print*{intg}
\end{align*}

出力

• 引数にa,bを入れるとaからbまでの定積分、入れなければ原始関数(積分定数なし)が出力されます。
• 原始関数が求まらない積分などは基本できなさそうです。

部分分数展開する： parfrac(num,den)

luacas_example.tex

\begin{CAS}
    vars('x')
	num = 3*x^2 - 9*x + 7
	den = x^4 - 7*x^3 + 18*x^2 - 20*x + 8
	p = parfrac(num, den)
\end{CAS}
\[ \print{num/den}=\print*{p} \]

出力

方程式の根を求める：　roots(f)

luacas_example.tex

\begin{CAS}
    vars('x')
	f = x^6 + 3*x^5 + 6*x^4 + 7*x^3 + 6*x^2 +3*x + 2
	r = roots(f)
\end{CAS}
$\print{f}=0$の解は
\[\lprint{r}\]

出力

• r[1]のようにすることで各要素にアクセスすることもできます（indexは1スタート）。

xについて解く： eq:solvefor(x)

luacas_example.tex

\begin{CAS}
	vars('x','y','z')
	lhs = e^(x^2*y)
	rhs = z + 1
	eq = Equation(lhs, rhs)
	eqx = eq:solvefor(x)
\end{CAS}
\[\print{eq}\iff\print{eqx}\]

出力

グラフをプロットする：　\fetch{f}(pgfplotsパッケージを利用)

luacas_example.tex

% 以下をプリアンプルに追加
% \usepackage{pgfplots}

\begin{CAS}
    vars('x')
	f = e^x
\end{CAS}
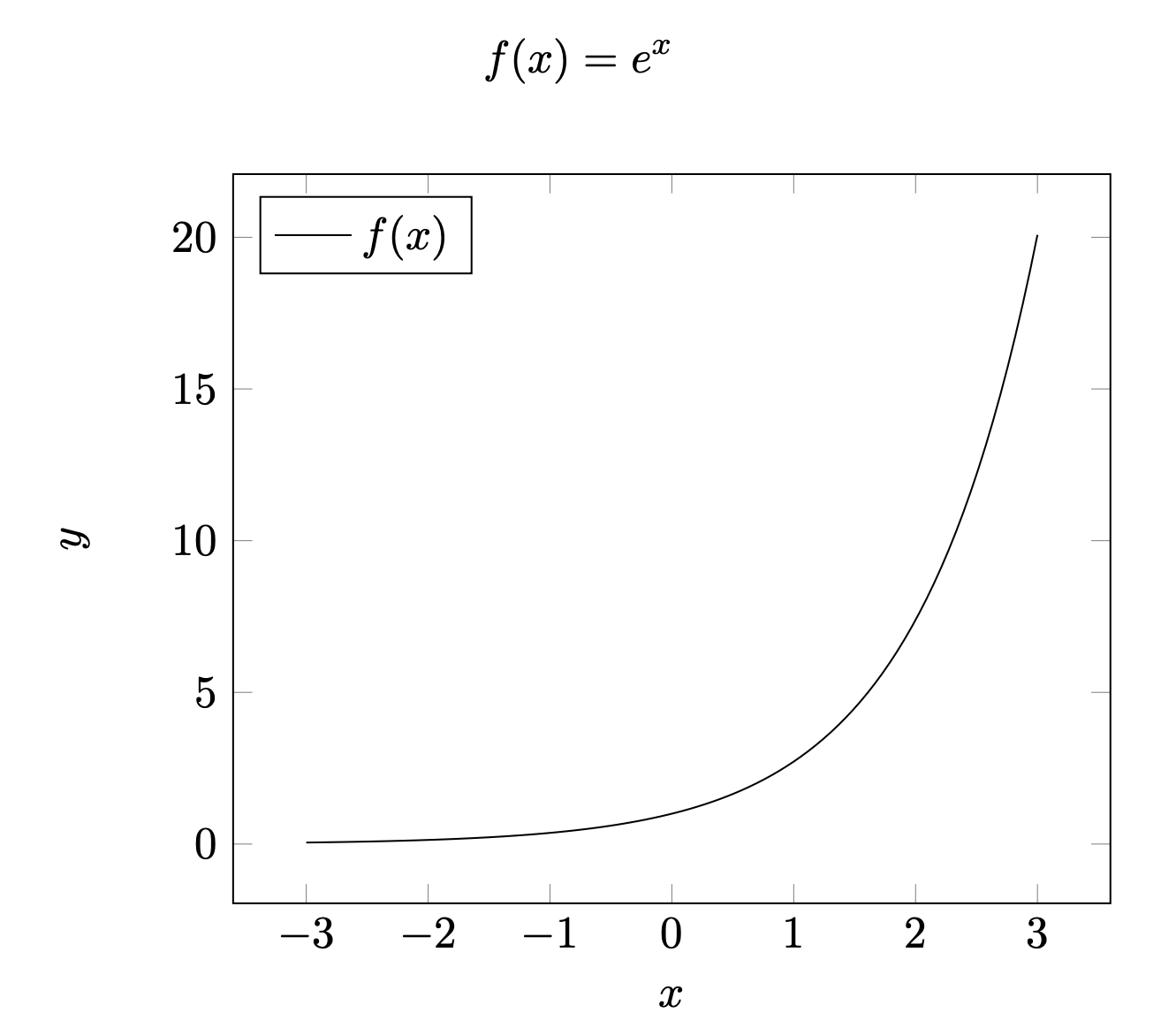
\[f(x)=\print{f}\]
\begin{figure}[H]
	\centering
	\begin{tikzpicture}
		\begin{axis}[legend pos = north west, xlabel=$x$, ylabel=$y$]
			\addplot[domain=-3:3,samples=100]{\fetch{f}};
			\addlegendentry{$f(x)$};
		\end{axis}
	\end{tikzpicture}
\end{figure}

出力

• pgfplots側の問題っぽいですが、$\ln(x)$とかは描画できませんでした。
• どうやらそのまま$\sin(x)$などを描画しようとするとxが度数法で見られるようです。

使用例: 関数の増減を調べる（関数定義・微分・根の計算・グラフの描画）

以下はluacasを使って書いてみました。

TeXコード（長いので折りたたみ）

luacas_example.tex

\begin{CAS}
	vars('x')
	f = x^3-5*x^2+2*x+1
	df = diff(f,x)
	r = roots(df)
\end{CAS}

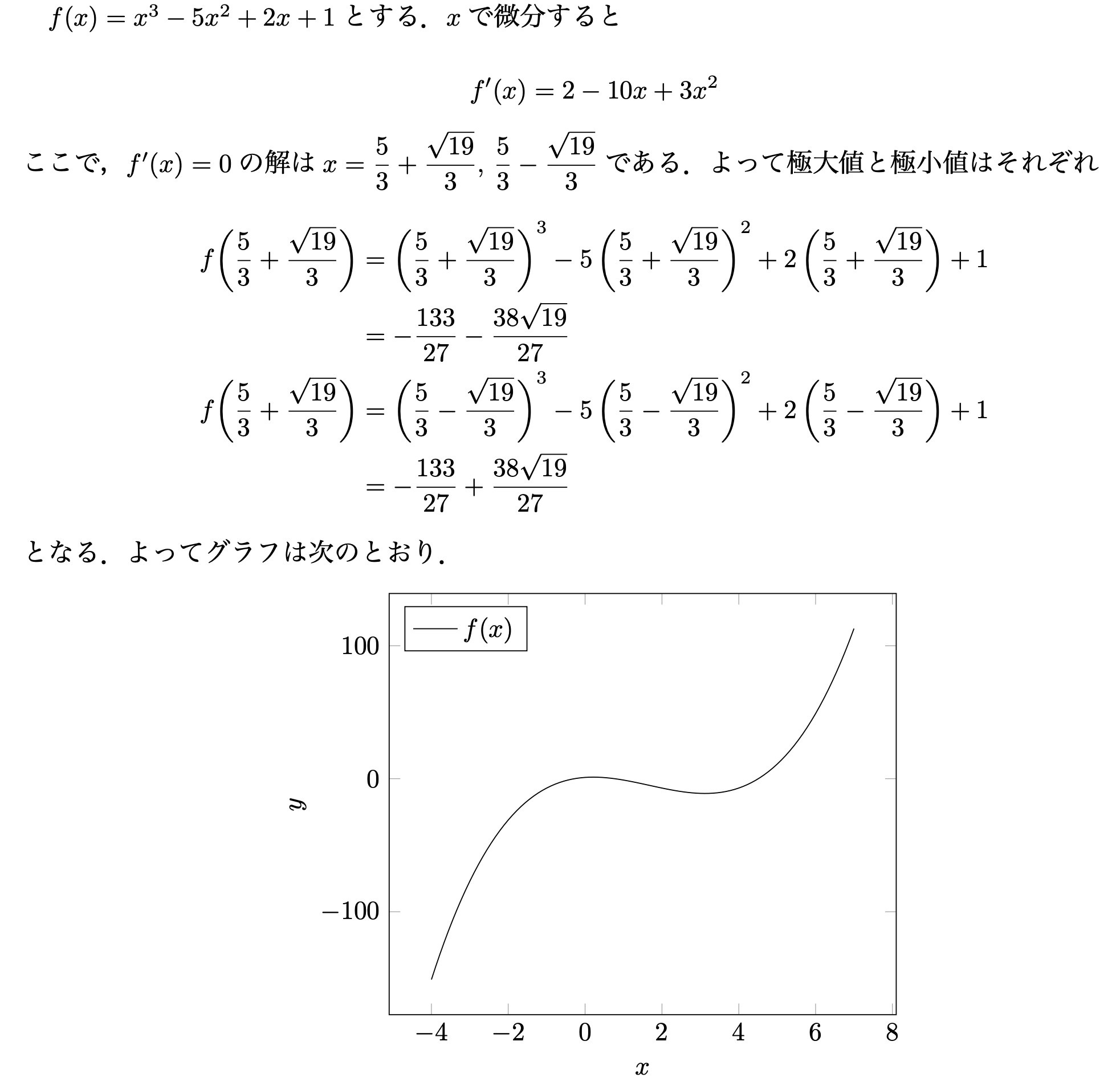
$f(x)=\print{f}$とする．$x$で微分すると
\[f'(x)=\print*{df}\]
ここで，$f'(x)=0$の解は$\displaystyle x=\print*{r[1]},\,\print*{r[2]}$である．
よって極大値と極小値はそれぞれ
\begin{align*}
	f\qty(\print*{r[1]}) & =\print{substitute({[x]=r[1]},f)}            \\
	                     & =\print{substitute({[x]=r[1]},f):simplify()} \\
	f\qty(\print*{r[1]}) & =\print{substitute({[x]=r[2]},f)}            \\
	                     & =\print{substitute({[x]=r[2]},f):simplify()}
\end{align*}
となる．よってグラフは次のとおり．
\begin{figure}[H]
	\centering
	\begin{tikzpicture}
		\begin{axis}[legend pos = north west, xlabel=$x$, ylabel=$y$]
			\addplot[domain=-4:7,samples=100]{\fetch{f}};
			\addlegendentry{$f(x)$};
		\end{axis}
	\end{tikzpicture}
\end{figure}

3. おわりに

luacasパッケージの紹介でした。LuaLaTeXは処理系にプログラミング言語Luaを組み込んでいるわけですが、それによってこんなにいろんな計算ができるというのは驚きですね。

このluacasパッケージが実際どの程度便利なのかは私もよくわからないですが（そんな使ってないので）、たとえそこまで便利じゃないと感じても面白ければまあ良いじゃんというのが私の考えです。

LuaLaTeXは他にも色々な可能性を秘めているLaTeXエンジンだと思うので、皆さんも是非LuaLaTeXの動向をチェックしてみてください。

最後になりましたが、明日以降の物工/計数 Advent Calender 2022の記事もお楽しみに。過去記事も色々面白いのあるのでぜひ見ていってください。

4. 改訂履歴