Pythonだと行列が計算できるらしい!
いや、他の言語でもforなんかでループさせれば出来るけど、numpyで簡単にできるらしいので試した。
x=np.array([[1, 2],
[1, 3]])
y=np.array([[2, 1],
[1, 3]])
z=x@y
z
# array([[ 4, 7],
# [ 5, 10]])
マジだ。最強か?
というわけで化学プロセスをグラフとみなして行列計算をしてみる。
以下はすべて等温・定容を仮定する。
その前に化学プロセスがどんな感じのもので、どのように計算されているか紹介する必要がある。今回は一番ありきたりな分離器付きリサイクル反応器の計算をする。
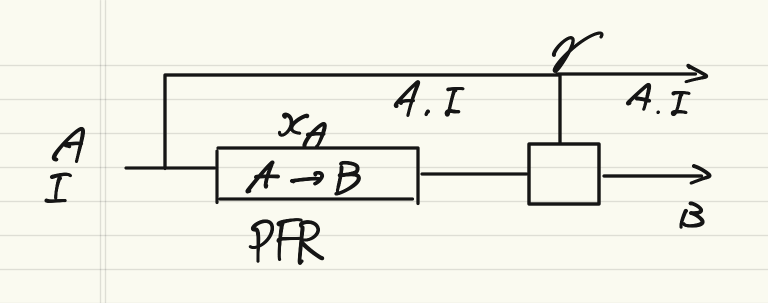
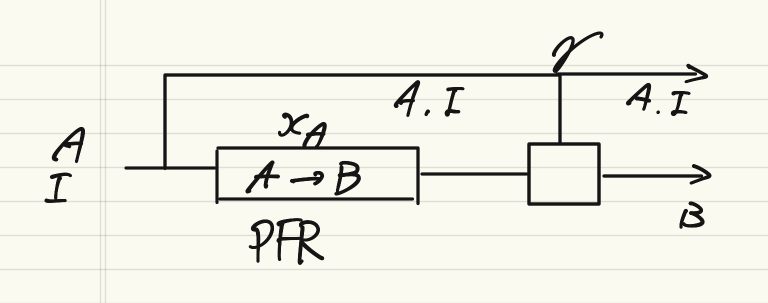
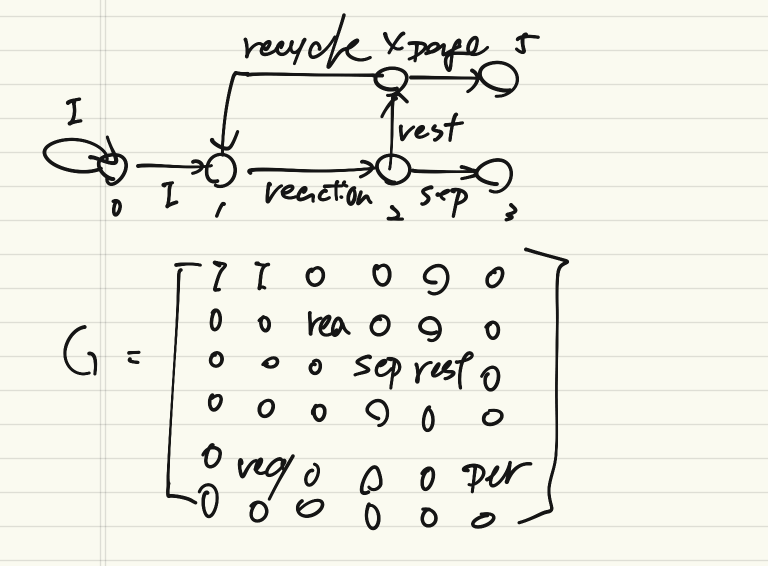
以下、そのイラスト。
入口から反応物A、不活性物質Iを流して、PFR(Plug Flow Reactor)でA→Bの反応を行う。出口でBを分離したのちにパージ率γに従ってA,Iは系外に捨てられる。残りはリサイクルされて入口に合流する。という流れになる。
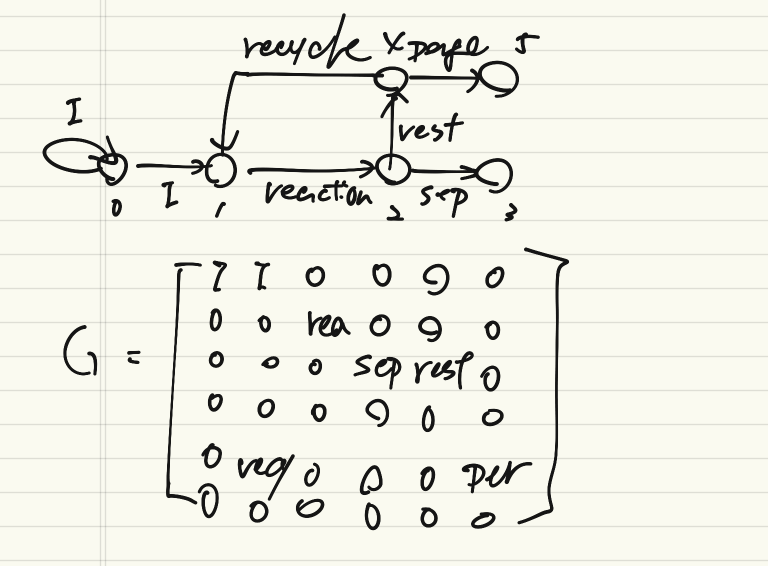
組成が変化する部分に点を置き、それらを線で結ぶことでプロセスを表現してみる。Gは有向グラフの隣接行列になる。ただし、反応による変化や分離操作を考えるため0,1ではなく実数値を取る。
プロセス流量の計算
上の式の流量計算は解析的に求められる(というより、ほとんどのプロセスは解析的に流量が分かる)。しかし、各部分で成立する物質収支に対する連立方程式を解く必要があるので割と面倒くさい。
実際にプロセスを管理する段ではExcelで収束計算させるのがとても使いやすい。しかし、Excelの欠点としてセル同士の計算に頼りきりなので局所的に書き替えて大失敗を起こしたりする。その上、プロセスを少し変えるだけで組みなおしたり、新しいファイルを作ったりする。
○○ver1.xlsm、○○ver2.xlsm、○○ver2-2.xlsm……みたいな地獄が発生する。
じゃあ、gitを使えばいい? gitを使いこなせてたらそもそも全作業をExcelに頼らない。化学系のITリテラシーは低い。
じゃあ何がしたいの?
行列に各地点での組成を要素とするベクトルを掛けることで流量のベクトルを算出したい。そのためにPythonの行列計算を行う。
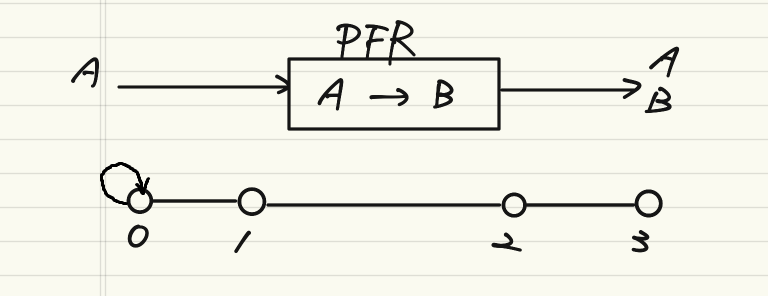
反応なしリサイクル反応器
入口からAを流し、特に処理をせず、出口のAを少しだけ入口に戻すだけのプロセス。
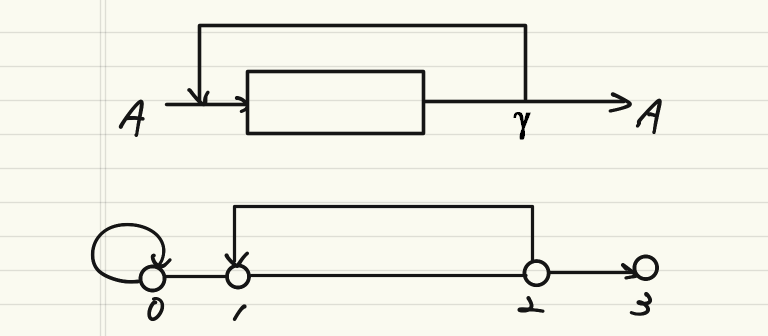
下段にグラフで表示したプロセスを描いているが、点0でループしているのは収束計算が必要になるため常に原料を供給するという意味でのループである。
これを計算してみる。
$$
\boldsymbol{F}=(1, 0, 0, 0)
$$
$$
\boldsymbol{G}=\begin{pmatrix}
1&1&0&0\
0&0&1&0\
0&1-\gamma&0&\gamma\
0&0&0&0
\end{pmatrix}
$$
流量(上の図ではAの流量)のベクトル$\boldsymbol{F}$は上のようになる。
一方で隣接行列$\boldsymbol{G}$は上のようになり、点3に対応する4行目は全て成分が0である。すなわち他の点への出力がないことを示している。
見て分かることだが、これは
$$
\boldsymbol{F’}=\boldsymbol{F}\times\boldsymbol{G}
$$
では計算できない。ある一定量が(何も反応させないが)反応器入口に返ってくるからである。
そこで、
$$
\boldsymbol{F_i}=\boldsymbol{F_{i-1}}\times\boldsymbol{G}
$$
として$\boldsymbol{F_i}-\boldsymbol{F_{i-1}}$が一定のerrorを下回るまで収束させる。
# 反応を伴わない場合
import numpy as np
# フローを有向グラフとして隣接行列を定義する
G=np.array([[1, 1, 0, 0],
[0, 0, 1, 0],
[0, 0.5, 0, 0.5],
[0, 0, 0, 0]])
# No.2のノードから1のノードに流量の0.5をリサイクルする
# 理論的には [1, (1/γ), (1/γ), 1]=[1, 2, 2, 1]
# フローの流量を定義
F=np.array([1, 0, 0, 0])
print(F)
# フローの収束計算をする
F_prev=F
F_out=F@G
print(F_out)
for i in range(30):
F_prev=F_out
F_out=F_out@G
if((F_out-F_prev<0.0001)).all():
print("{}回目に収束しました".format(i+2))
print(F_out)
break
if(i%5==0):print(F_out)
'''
[1 0 0 0]
[1. 1. 0. 0.]
[1. 1. 1. 0.]
[1. 1.875 1.75 0.875]
[1. 1.96875 1.96875 0.96875]
[1. 1.99609375 1.9921875 0.99609375]
[1. 1.99902344 1.99902344 0.99902344]
[1. 1.99987793 1.99975586 0.99987793]
29回目に収束しました
[1. 1.99993896 1.99987793 0.99993896]
'''
といった感じの結果となる。1000回計算、0.000001の誤差程度なら一瞬なので問題ないだろう。
理論的解法
$$
F_1 = F_0 + (1-\gamma)F_2 \
F_2 = F_1 \
F_3 = \gamma F_2
$$
簡単なフローなので以上の連立方程式を解けば反応器内の流量が$F_1=F_0/\gamma$であることが分かる。収束計算では$F=(1, 2, 2, 1)$に収束していることが分かる。
反応あり反応器
前述のリサイクル反応器に比べるとだいぶ難易度が落ちるように思えるが$A \rightarrow B$の反応による変化、およびA,Bの多成分系なので少し難しい。
$$
\boldsymbol{F}= \begin{pmatrix}
1&0&0&0 \
0&0&0&0
\end{pmatrix}
$$
$$
\boldsymbol{G}=\begin{pmatrix}
\boldsymbol{I}&\boldsymbol{I}&\boldsymbol{0}&\boldsymbol{0}\
\boldsymbol{0}&\boldsymbol{0}&\boldsymbol{reaction}&\boldsymbol{0}\
\boldsymbol{0}&\boldsymbol{0}&\boldsymbol{0}&\boldsymbol{I}\
\boldsymbol{0}&\boldsymbol{0}&\boldsymbol{0}&\boldsymbol{0}
\end{pmatrix}
$$
ここで$\boldsymbol{I}, \boldsymbol{0}, \boldsymbol{reaction}$はそれぞれ、
$$
\boldsymbol{I}=\begin{pmatrix}
1&0\
0&1
\end{pmatrix}
$$
$$
\boldsymbol{0}=\begin{pmatrix}
0&0\
0&0
\end{pmatrix}
$$
$$
\boldsymbol{reaction}=\begin{pmatrix}
1-conversion&0\
conversion&1
\end{pmatrix}
$$
で定義される。($conversion$は反応率)
$A,B$を独立な成分としてそれぞれ隣接行列$\boldsymbol{G}$を定義してもよいが、$\boldsymbol{reaction}$のように流量成分$F_j$を掛けるだけで$A$と$B$の流量を1度に計算できるメリットが大きい。また$\boldsymbol{reaction}$行列の列成分は合計が1で保存されるのでその確認も行いやすい。
ただし、ここでは
$$
\boldsymbol{F_i}=\boldsymbol{F_{i-1}}\times\boldsymbol{G}
$$
に対して収束計算を行うわけにはいかない。Gが4階のテンソルになるので出力が$4×4×4$の行列になってしまう。
正しい出力は$\boldsymbol{F}$の行成分$F_j$に対して$\boldsymbol{G}$の列成分$G_{jk}$が作用することなので、点$k$に対して、
$$
F_j^i=\sum_{j}F_j^{i-1}\times G_{jk}
$$
を計算していく。上付きのiはi番目の収束計算を示している。
# リサイクルを伴わない場合
# フローを有向グラフとして隣接行列を定義する(多成分系ではテンソルとなる)
zero=np.array([[0, 0],
[0, 0]],dtype=np.float64)
Identity=np.array([[1, 0],
[0, 1]],dtype=np.float64)
reaction=np.array([[0.2, 0.8],
[0, 1]],dtype=np.float64)
G=np.array([[Identity, Identity, zero, zero],
[zero, zero, reaction, zero],
[zero, zero, zero, Identity],
[zero, zero, zero, zero]],dtype=np.float64)
# フローの流量を定義
F=np.array([[1, 0], [0, 0], [0, 0], [0, 0]],dtype=np.float64)
F_prev=np.zeros([4, 2],dtype=np.float64)
for k in range(50):
for i in range(len(G)):
sum_Fi=np.array([0, 0], dtype=np.float64)
F_prev=np.copy(F)
for j in range(len(G)):
sum_Fi+=F[j]@G[j][i]
F[i]=sum_Fi
if((abs(F_prev-F)<0.00001).all()):
print("収束しました")
print(F)
break
'''
収束しました
[[1. 0. ]
[1. 0. ]
[0.2 0.8]
[0.2 0.8]]
'''
単純にリサイクルのない反応器なので反応率がそのまま出てくる。各点の流量を計算する分、3回で収束する。
分離器付きリサイクル反応器
化学プロセスで一番ありふれた反応プロセスで冒頭に示したプロセスである。
反応物$A$に対して生成物$B$が生成し、プロセス全体に不活性成分$I$が流れる。分離器で製品$B$のみが分離されたフローは系外に捨てられるパージとリサイクルに分けられる。3成分系のプロセスである。
理論計算
成分$A$についての流量は以下の連立方程式による。
$$
F_{A1} = F_{A0} + (1-\gamma)F_{A4} \
F_{A2} = (1-conversion) \times F_{A1} \
F_{A3} = 0 \
F_{A4} = F_{A3} \
F_{A5} = \gamma \times F_{A4}
$$
成分$B$については
$$
F_{B3} = conversion \times F_{A1}
$$
成分$I$については
$$
F_{I1} = F_{I0} + (1-\gamma)F_{I4} \
F_{I2} = F_{I1} \
F_{I3} = 0 \
F_{I4} = F_{I3} \
F_{I5} = \gamma \times F_{I4}
$$
を解くことで得られる。これだけで割と面倒なことが分かる。
行列
Pythonで行列計算をする要領は先ほどと変わらない。$A=1, I=2$の初期流量でやってみる。
$$
\boldsymbol{F}= \begin{pmatrix}
1&0&0&0&0 \
0&0&0&0&0 \
2&0&0&0&0
\end{pmatrix}
$$
$$
\boldsymbol{G}=\begin{pmatrix}
\boldsymbol{I}&\boldsymbol{I}&\boldsymbol{0}&\boldsymbol{0}&\boldsymbol{0}&\boldsymbol{0}\
\boldsymbol{0}&\boldsymbol{0}&\boldsymbol{reaction}&\boldsymbol{0}&\boldsymbol{0}&\boldsymbol{0}\
\boldsymbol{0}&\boldsymbol{0}&\boldsymbol{0}&\boldsymbol{product}&\boldsymbol{separation}&\boldsymbol{0}\
\boldsymbol{0}&\boldsymbol{0}&\boldsymbol{0}&\boldsymbol{0}&\boldsymbol{0}&\boldsymbol{0}\
\boldsymbol{0}&\boldsymbol{recycle}&\boldsymbol{0}&\boldsymbol{0}&\boldsymbol{0}&\boldsymbol{perge}\
\boldsymbol{0}&\boldsymbol{0}&\boldsymbol{0}&\boldsymbol{0}&\boldsymbol{0}&\boldsymbol{0}
\end{pmatrix}
$$
ここで$\boldsymbol{I}, \boldsymbol{0}, \boldsymbol{reaction} ,\dots$はそれぞれ、
$$
\boldsymbol{I}=\begin{pmatrix}
1&0&0\
0&1&0\
0&0&1
\end{pmatrix}
$$
$$
\boldsymbol{0}=\begin{pmatrix}
0&0&0\
0&0&0\
0&0&0
\end{pmatrix}
$$
$$
\boldsymbol{reaction}=\begin{pmatrix}
1-conversion&0&0\
conversion&1&0\
0&0&1
\end{pmatrix}
$$
$$
\boldsymbol{product}=\begin{pmatrix}
0&0&0\
0&1&0\
0&0&0
\end{pmatrix}
$$
$$
\boldsymbol{separation}=\begin{pmatrix}
1&0&0\
0&0&0\
0&0&1
\end{pmatrix}
$$
$$
\boldsymbol{perge}=\begin{pmatrix}
\gamma &0&0\
0&\gamma &0\
0&0&\gamma
\end{pmatrix}
$$
$$
\boldsymbol{recycle}=\begin{pmatrix}
1-\gamma &0&0\
0&1-\gamma &0\
0&0&1-\gamma
\end{pmatrix}
$$
先ほどの方針と同じく流量の行成分と隣接行列(テンソル)の列成分の行列を作用させた和を取る。
$$
F_j^i=\sum_{j}F_j^{i-1}\times G_{jk}
$$
計算
収束計算を行ったプログラムがこちら。
def graph_dia(gamm, conversion):
zero=np.array([[0, 0, 0],
[0, 0, 0],
[0, 0, 0]],dtype=np.float64)
Identity=np.array([[1, 0, 0],
[0, 1, 0],
[0, 0, 1]],dtype=np.float64)
reaction=np.array([[1-conversion, conversion, 0],
[0, 1, 0],
[0, 0, 1]],dtype=np.float64)
perge=np.array([[gamm, 0, 0],
[0, gamm, 0],
[0, 0, gamm]],dtype=np.float64)
recycle=np.array([[1-gamm, 0, 0],
[0, 1-gamm, 0],
[0, 0, 1-gamm]],dtype=np.float64)
separation=np.array([[1, 0 ,0],
[0, 0, 0],
[0, 0, 1]], dtype=np.float64)
product=np.array([[0, 0, 0],
[0, 1, 0],
[0, 0, 0]], dtype=np.float64)
G=np.array([[Identity, Identity, zero , zero , zero , zero ],
[zero , zero , reaction, zero , zero , zero ],
[zero , zero , zero , product, separation, zero ],
[zero , zero , zero , zero , zero , zero ],
[zero , recycle , zero , zero , zero , perge],
[zero , zero , zero , zero , zero , zero ]],dtype=np.float64)
return G
行列の計算式は上のように定義。
def flow_cal(G, F, number, error):
flag=False
for k in range(number):
for i in range(len(G)):
sum_Fi=np.zeros(len(F[0]), dtype=np.float64)
if(k%100==0): F_prev=np.copy(F)
for j in range(len(G)):
sum_Fi+=F[j]@G[j][i]
F[i]=sum_Fi
if((abs(F_prev-F)<error).all()):
break
if(k==number-1): flag=True
return F, flag
収束計算の関数は上のようになる。flagで収束の有り無しを判断する。
これらを用いて収束計算をしてみる。
# 反応・リサイクル・分離器あり
np.set_printoptions(precision=5, suppress=True)
gamm=0.1
conversion=0.5
G=graph_dia(gamm, conversion)
# フローの流量を定義
num_composition=3
F=np.zeros([len(G), num_composition],dtype=np.float64)
F[0]=[1, 0, 2]
F_prev=np.zeros([len(G), num_composition],dtype=np.float64)
flow_cal(G, F , 1000, 0.0000001)
'''
(array([[ 1. , 0. , 2. ],
[ 1.81818, 0. , 20. ],
[ 0.90909, 0.90909, 20. ],
[ 0. , 0.90909, 0. ],
[ 0.90909, 0. , 20. ],
[ 0.09091, 0. , 2. ]]), False)
'''
点3と点5に相当する4行目と6行目の和が3になっていることから収束計算がうまくいっていることが分かる。実際に前述の連立方程式を解くことで各点での流量が正しいことが分かる。
パージ率の作用
パージ率を変えた時の反応器内流量の変化を描画してみる。
num_composition=3
F=np.zeros([len(G), num_composition],dtype=np.float64)
F[0]=[1, 0, 2]
F_prev=np.zeros([len(G), num_composition],dtype=np.float64)
gamma=np.linspace(0.01, 1, 100)
conversion=0.5
Total_flow=[]
B_flow=[]
Flow_ammount=[]
for i in range(len(gamma)):
gamm=gamma[i]
conversion=0.5
G=graph_dia(gamm, conversion)
#フローの流量を定義
num_composition=3
F=np.zeros([len(G), num_composition],dtype=np.float64)
F[0]=[1, 0, 2]
F_prev=np.zeros([len(G), num_composition],dtype=np.float64)
Total_flow.append(flow_cal(G, F , 2000, 0.000001))
B_flow.append(Total_flow[i][0][3][1])
Flow_ammount.append(sum(Total_flow[i][0][2]))
if(Total_flow[i][1]):
print("収束しませんでした。{}回目".format(i))
break
plt.figure(figsize=(16, 8))
plt.subplot(1,2,1)
plt.plot(gamma, B_flow)
plt.subplot(1,2,2)
plt.plot(gamma, Flow_ammount)
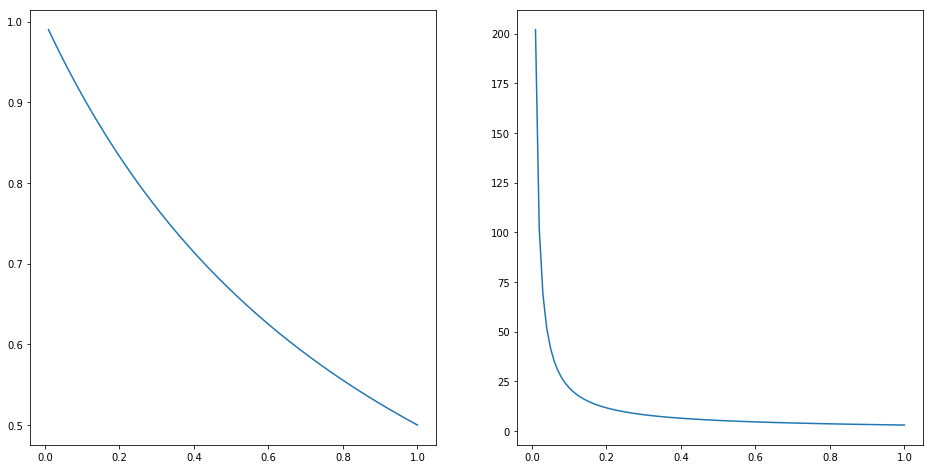
左がパージ率に対する$B$の生成量、右が反応器の全流量になる。
パージ率が無限小ならば原料$A$はリサイクルされて反応器入口に入り最終的に$B$として系外に出る。一方で成分$I$は系外に排出されずに反応器に蓄積し続けるので無限大になる。
逆にパージ率1ではリサイクルなし反応器と変わらない。$F_B=0.5$。
当然、$B$の反応率は大きいほうがいいのでパージ率は下げるべきだが、一方で反応器内の流量が大きくなるので装置コストがかさむ。大抵はこれを計算してコストのパレート最適を取る。
まとめ
グラフの隣接行列と行列計算を用いて化学プロセスの流量を収束計算で求めるプログラムを作製した。
利点として、
- フロー計算の度にExcelファイルを量産しなくて済む
- 各点の流量が行列として得られる
- 流量行列に製品価格や装置コストを作用させることでコストを見積もることができる?
- $\gamma$を変化させた時のように反応率などを流量や温度の関数として自由に書ける
- $G$は$dev(G) \times dev(G)$と大きくなるが視覚的に分かりやすい
- コスト計算、反応計算、流量計算といったクラスで分けられるので使い勝手が良い(はず?)
と列挙してみたが、そこまで使い勝手が良いかはわからない。少なくとも大学では連立方程式の方を教えられるが、実際はExcelの収束計算を使っていたりするのでどれが正解か分からない。
でも、わたしゃもうExcel+VBAでRG法プログラムを作りたくはないのじゃ……