【DAG】DAGの二重支払いを防ぐ仕組み（１）Avalancheまでの道

はじめに

　DAGの二重支払いを防ぐ仕組みについてこれから三つの記事に分けて紹介していきたい。

1. Avalancheまでの道：Avalancheを理解するためのSlush、Snowflake、Snowball。
2. Avalanche：Avalancheを詳しく見る回。
3. Coordicide: IOTAの取る予定のアプローチ。

DAGとコンセンサス

　ブロックチェーンは下記の図のようにトランザクション（四角）をブロックに格納してブロックを繋いでいく。トランザクション処理能力はブロックの容量に依存している。これの解決方法としてブロックのサイズを大きくすることは古くから提案されており、その意見対立でBitcoinからBitcoin Cash(BCH)が分裂・誕生したのはご存知の通りだ。

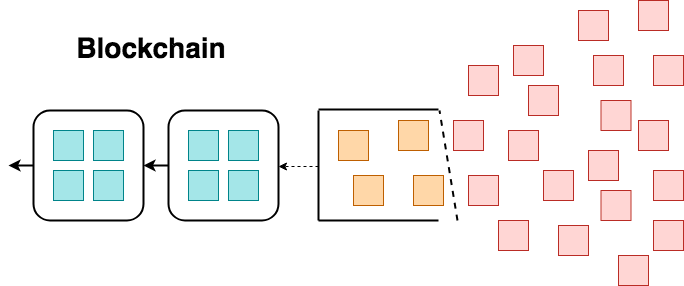
　また、ブロックチェーンをいわば最終決定機関として、小さなアプリケーションレベルのレイヤーをサブチェーン、サイドチェーンに任せることにより、全体としてトランザクション処理能力を損なわないようにスケールする仕組みとして、EthereumのPlasma、また、異なるチェーン間の通信を可能にするCosmosなどがある。
　また、Ethereum 2.0ではチェーン自体を複数用意（シャーディング）し、それを束ねるビーコンチェーンというアイデアが採用され、開発も現在進行中である。（実際はビーコンチェーンが先に実装され、テストネットでは稼働中である。）

　これらはブロックチェーンを使うことを前提としている。しかし、先ほど述べたようなブロックチェーンの欠点の原因がブロックチェーン自体にあるという前提でそれを否定し、新しいデータ構造であるDAGを用いて分散型台帳を実現しようとしている取り組みがある。DAGとは下図のようにトランザクションをブロックに格納する行為がなく、トランザクション自体が過去のトランザクションを参照する連続によってブロックチェーンの特徴である改竄耐性を実現しつつスケーラビリティを克服できると言われている。

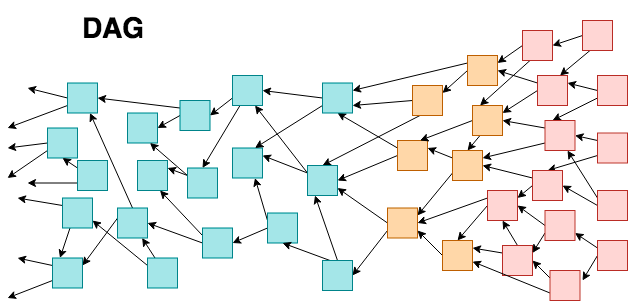
　ただもちろんDAGにも課題がある。その一つとしてはP2Pネットワーク全体が同じ台帳を保持しそのコンセンサスを取るのがブロックチェーンに比べて困難であるということが挙げられる。P2Pネットワークでは、それを構成するノードが各々のタイミングで新しいトランザクションを台帳に書き込む。もし、ネットワークの異なる場所でほぼ同時に矛盾するトランザクション（暗号通貨なら二重支払い）が書き込まれた場合、その両方が台帳に存在する状態が出来上がる。
　ブロックチェーンの場合、矛盾するトランザクションを書き込むリクエストが来た時に、矛盾トランザクションは同じブロックに入れる時に一つだけ選ぶこと、過去のブロック全てと見比べることの二つの約束を守ることによって、複数の矛盾するリクエストを台帳に書き込むことは最終的に防げる。
　しかし、DAGではトランザクションは即座に台帳に反映され、次に来たトランザクションが矛盾トランザクションを次から次へと参照することで、いつの間にかDAGの奥に存在したまま埋もれてしまうことがありうる。
　これを防ぐにはDAGが長くなる過程で、矛盾する複数のトランザクションの中から一つだけを選択し、P2Pネットワーク全体が同じ選択に収束する仕組みが必要になる。
　その解決方法は静かにだが研究・開発されており、IOTAはCoordicide、AVA LabsはAvalancheというコンセンサス方式を提案している。本シリーズではこれら二大勢力の主張するコンセンサス方式について簡単に紹介したい。

Athereum

　AthereumはAva-labsが開発するEthrereumからソフトフォークより優しくフォークする（彼らはスプーンと呼ぶ）ことでEtherreumをDAG化することを目的とするプロジェクトである。今年のEthereum Devconでテストネットのスタートを発表して名が広く伝わった。現存する多くの議論と同じく、tpsを上げるという目的を、DAG化することにより達成することを目指しているようだ。
　Athereumの何がAなのかは、選択したコンセンサスアルゴリズムがAvalancheと呼ばれていることによる。AvalancheはTeam Rocketという匿名の名の下論文として世に出たDAGをベースとしたプロトコルである。Avalancheは、P2Pネットワーク上で分散型台帳の状態が一時的に発散しても、やがて必ず共通の解に収束する性質をMetastability（メタ安定性）と呼ぶ。そしてAvalancheはこのメタ安定性を中心的役割を持つマスターノードのような機構を持たずとも実現するためのコンセンサスアルゴリズムという訳だ。
　論文では、Avalancheを語る上で基本となるシンプルな3つのアルゴリズムを紹介している。それらは

1. Slush（溶けた雪）
2. Snowflake（雪片）
3. Snowball（雪玉）

と名付けられる。Avalanche（雪崩）はこのうちSnowballをDAG上でどう使うかを説いた手法となる。
　本記事ではこのAvalancheがすんなり理解できるように論文と同じ順序でSlushから話を始めることにする。

問題の前提

　ただ、実際に解説に入る前に、今回の問題設定を先に記す。
　台帳上に存在する、二重支払いのような矛盾トランザクション群$T_0, T_1..., T_m$がある。このセットを$P_{T_0}$とする。ちなみに$T_0, T_1...,T_m$は全て平等であるため、$P_{T_0}=P_{T_1}=...=P_{T_m}$である。
　メタ安定性とは、P2Pネットワーク上の全てのノードが有限時間内に、一つの$T_i\in P_{T_0}（ 0\le i\le m）$を必ず選ぶことが保証される性質である。

Slush

　まず問題を単純化し、矛盾するトランザクションが2つ（Red、Blue）だけある場合で話をする。
　Slushは非常にシンプルである。

1. あるノードが別のノードからトランザクションを教えられる。この時点でこのノードは他のノードがこのトランザクションと矛盾しているものを持っていないか、もし矛盾していたら皆どれ（今回はRed or Blue）を選んだを確かめる必要がある。
2. そこでノードはネットワーク上の$k$個の別のノードを選ぶ。
3. それらに対して自分の色を教えた後、どのトランザクション$T_i\in \{ T_{Red}, T_{Blue} \} $を選んだかを聞き、その結果として回数$Count(T_{Red}), Count(T_{Blue})$をカウントする。
4. もしその回数が閾値$\alpha k$以上なら自身のトランザクションをその色にする。

　以下は論文から引用したSlushのアルゴリズムである。

　また、論文を参考にPythonで実装したものがこれになる。

slush.py

def iterate(self):
    random.shuffle(self.queue)
    for i in self.queue:

        if self.nodes[i].color == COLOR_INIT:
            continue

        sample = random.sample([x for x in range(self.size) if x != i], k=K)
        count = {COLOR_RED: 0, COLOR_BLUE: 0}

        # counting
        for node_index in sample:
            response = self.nodes[node_index].on_query(self.nodes[i].color)
            if response == COLOR_RED:
                count[COLOR_RED] += 1
            elif response == COLOR_BLUE:
                count[COLOR_BLUE] += 1

        # color updates
        for color in [COLOR_RED, COLOR_BLUE]:
            if count[color] >= THRESHOLD*len(sample):
                self.nodes[i].set(color)

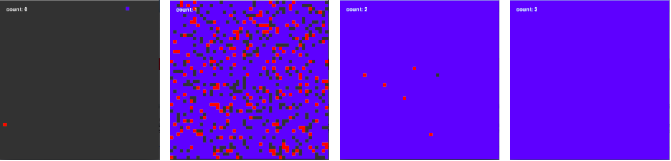
　下図は時間の経過とともに、ノード（１マス）が色を決定する過程を図にしたもの。今回はRedが選ばれたようだ。

　また、下のように青が選ばれる場合もあり、収束までの時間も一定ではない。

Snowflake

SnowflakeはSlushの改善版でありビザンチン耐性を持つ。主な変更点として、ノードがネットワークから色の多数決をとるとき、その結果がある回数連続で同じものが続いたときに自信の状態を最終的に決定する点である。そのためノードは内部的に回数を保持しておくようにするのだ。

1. あるノードが別のノードからトランザクションを教えられる。この時点でこのノードは他のノードがこのトランザクションと矛盾しているものを持っていないか、もし矛盾していたら皆どれ（今回はRed or Blue）を選んだを確かめる必要がある。
2. そこでノードはネットワーク上の$k$個の別のノードを選ぶ。
3. それらに対して自分の色を教えた後、どのトランザクション$T_i\in \{ T_{Red}, T_{Blue} \} $を選んだかを聞き、その結果として回数$Count(T_{Red}), Count(T_{Blue})$をカウントする。
4. もしその回数が閾値$\alpha k$以上で、その結果多数派の色が自分の色と同等なら内部カウントを１プラスする。もし異なる場合は０にリセットする。
5. 内部カウントが一定以上に達したら自分の最終的な色を決定する。

snowflake.py

def iterate(self):
    random.shuffle(self.queue)
    for i in self.queue:

        if self.nodes[i].color == COLOR_INIT:
            continue

        if self.nodes[i].decided == 1:
            continue

        sample = random.sample([x for x in range(self.size) if x != i], k=K)
        count = {COLOR_RED: 0, COLOR_BLUE: 0}

        # counting
        for node_index in sample:
            response = self.nodes[node_index].on_query(self.nodes[i].color)
            if response == COLOR_RED:
                count[COLOR_RED] += 1
            elif response == COLOR_BLUE:
                count[COLOR_BLUE] += 1

        # color, count updates
        for color in [COLOR_RED, COLOR_BLUE]:
            if count[color] >= THRESHOLD*len(sample):
                if color != self.nodes[i].color:
                    self.nodes[i].set(color)
                    self.nodes[i].count = 0
                else:
                    self.nodes[i].count += 1
                    if self.nodes[i].count > COUNT:
                        self.nodes[i].decided = 1

Snowball

　Snowflakeを改善したのがsnowballである。snowballでは色に対する信頼度という概念を増やす。多数派アンケートの結果のたびに多数派色の信頼度を上げ、自身の暫定色を決める。暫定色がひっくり返るたびに、負けた色の信頼度は０にリセットされ、何度かのアンケートを経ても信頼度を失わずに一定の水準に達した色が最終的な自身の色となる。

1. あるノードが別のノードからトランザクションを教えられる。この時点でこのノードは他のノードがこのトランザクションと矛盾しているものを持っていないか、もし矛盾していたら皆どれ（今回はRed or Blue）を選んだを確かめる必要がある。
2. そこでノードはネットワーク上の$k$個の別のノードを選ぶ。
3. それらに対して自分の色を教えた後、どのトランザクション$T_i\in \{ T_{Red}, T_{Blue} \} $を選んだかを聞き、その結果として回数$Count(T_{Red}), Count(T_{Blue})$をカウントする。
4. もしその回数が閾値$\alpha k$以上で、その結果の多数派の色に対する信頼度を１プラスする。
5. もしその結果信頼度が高い色が自身の暫定色に対する信頼度を上回ったら、自身の暫定色を更新し、更新前の自身の暫定色に対する信頼度を０にリセットする。
6. いづれかの色に対する信頼度が一定以上に達したらその色を最終的なものとして選ぶ。

snowball.py

def iterate(self):
    random.shuffle(self.queue)
    for i in self.queue:

        if self.nodes[i].color == COLOR_INIT:
            continue

        if self.nodes[i].decided == 1:
            continue

        sample = random.sample([x for x in range(self.size) if x != i], k=K)
        count = {COLOR_RED: 0, COLOR_BLUE: 0}

        # counting
        for node_index in sample:
            response = self.nodes[node_index].on_query(self.nodes[i].color)
            if response == COLOR_RED:
                count[COLOR_RED] += 1
            elif response == COLOR_BLUE:
                count[COLOR_BLUE] += 1

        # color, count, confidence updates
        for color in [COLOR_RED, COLOR_BLUE]:
            if count[color] >= THRESHOLD*len(sample):
                self.nodes[i].d[color] += 1

                if self.nodes[i].d[color] > self.nodes[i].d[self.nodes[i].color]:
                    self.nodes[i].set(color)

                if color != self.nodes[i].last_color:
                    self.nodes[i].last_color = color
                    self.nodes[i].count = 0
                else:
                    self.nodes[i].count += 1
                    if self.nodes[i].count > COUNT:
                        self.nodes[i].decided = 1

予告編

Avalancheは今回説明したSnowballをDAG上で実現する仕組みである。これについてはまた別に紹介する予定。（最近忙しいのでいつになるか分からない。。。）早く知りたい人のために有用なリンクを並べておく。

• Avalancheの仕組み：https://hackernoon.com/protocol-spotlight-avalanche-part-2-80cd4a530b6b
• AvalancheとIOTA Coordicideの比較：https://nearprotocol.com/blog/avalanche-vs-the-new-iota-consensus-algorithm-with-a-touch-of-spacemesh/