アトミック・スワップ(Atomic Swap)とは、異なるチェーン間で、第三者への信頼なしに、暗号通貨同士を交換する技術である。ミソとなるのがまず、異なるチェーン間という点。これは、ERC20トークン同士の交換とは意味が違う。例えばWETHとCOMPといった異なるERC20トークンの交換は、UniswapなどのDEXによってトラストレスに行える。が、BTCとETHといった異なるチェーンに乗ったトークンの交換には暗号通貨取引所を介するなど、第三者に取引の信頼を置いて行う必要がある。アトミック・スワップは異なるチェーン間のコイン交換を第三者の介入無くしてユーザー間だけで実現するプロトコルである。本記事では、BitcoinとMoneroの間で行われるアトミック・スワップの技術について説明していく。
a = 100
b = 20
thirdPerson = a <--- 誰かに信頼を置く
a = b
b = thirdPerson
a = 100
b = 20
a, b = b, a <--- 仲介者がいない
今回紹介するプロトコルで新しいのは、ワンタイム検証可能暗号化署名(アダプター署名)と言う技術を使って、スマートコントラクトなどを使わずに、純粋な暗号技術の組み合わせと少しのBitcoinスクリプトのみで、アトミック・スワップを実現した点である。また、異なる楕円曲線を使う(BTCは$secp256k1$、XMRは$ed25519$)通貨間であっても異なる楕円曲線の離散対数の同等証明という技術と組み合わせることで実現できた。
ちなみに元本はこちら
導入
検証可能暗号化署名(VES: Verifiable Encrypted Signature)
以下の3つのアルゴリズムで構成される。アルファベットの大文字は公開鍵、小文字は秘密鍵と考えて良い。(メッセージ$m$は除く。)
- $EncSign(x,Y,m)\rightarrow\hat{\sigma}$:署名者の秘密鍵$x$でメッセージ$m$を署名する際、公証人公開鍵$Y$で暗号化する。そして得られる暗号化された署名を$\hat{\sigma}$とする。勘違いしてはいけないのが、これは$Enc(Y,Sign(x,m))$とは違い、$EncSign$した本人も生の署名$\sigma$は分からない。
- $EncVerify(X,Y,m,\hat{\sigma})\rightarrow 0,1$:メッセージ$m$に付随する暗号化された署名$\hat{\sigma}$が本当に公開鍵$X$の秘密鍵によって署名されて、公証人鍵$Y$で暗号化されたかを検証する。成功したら$1$、失敗すれば$0$を返す。
- $DecSig(y,\hat{\sigma})\rightarrow\sigma$:公証人の秘密鍵で暗号化された署名$\hat{\sigma}$を複合して生の署名$\sigma$を返す。もちろんこの$\sigma$は$X$によって署名されたことを普通の署名検証にかければ確認できる。
普通の署名では、署名者Aが秘密鍵$x_a$でメッセージ$m$を署名して署名$\sigma$を作り、検証者BがAの公開鍵$X_a$で$\sigma$を検証し、本当に$\sigma$がAによって作られたかを検証する。
しかし、検証可能暗号化署名(以下VESとする)では、公証人Cの公開鍵$X_c$で暗号化されて署名「$\hat{\sigma_{c}}=EncSign(x_a,X_c,m)$」される。この場合、生の署名はAにもBにも明かされないが、$EncVerify(\hat{\sigma_c},X_c,m)$という計算で、$EncSign$された署名はAさんに署名されてCさんが保証していることを確認できる。そして、$\sigma=DecSig(\hat{\sigma_c},x_c)$という計算をCさんが行うことで、生の署名$\sigma$を得ることができる。
ワンタイム検証可能暗号化署名(One-Time VES, O-VES, Adapter Signature, アダプター署名)
アダプター署名と呼ぶことにするこの署名方式は一個前のセクションで紹介したVESに以下2つのアルゴリズムを追加したものである。
- $RecKey(Y,\hat{\sigma})\rightarrow\delta$:公証人公開鍵とそれで暗号化された署名$\hat{\sigma}$からリカバリーキー$\delta$を導き出す操作。
- $Rec(\sigma,\delta)\rightarrow y$:生の署名$\sigma$とリカバリーキーから、公証人鍵の秘密鍵$y$を逆算する。
ワンタイムという通り、VESの公証人の鍵$X_c$の使用回数を一回きりにしたもの。つまり$\sigma$と$\hat{\sigma_c}$から$x_c$が逆算できる。そのため一度$DecSig$されて生の署名が公開されると、公証人の鍵ペア($X_c$, $x_c$)はもう使えなくなる。
基本的なプロトコル
アダプター署名を使うとなぜトラストレスなアトミック・スワップが可能になるのか。その基本的な仕組みをこれから説明していく。
ざっくりとした流れ
コインXとコインYのアトミックスワップで、AさんはXを欲しくて、BさんはYを欲しい場合。また、XとYの署名に使われる楕円曲線は同じだとする。AはX用公開鍵$X_a=x_aG$、Y用公開鍵$Y_a=y_aG$を生成し、Bもそれぞれ$X_b=x_bG$、$Y_b=y_bG$を生成する。
- Bは、$X_a$と$X_b$のマルチシグアドレス$X_{ab}$に
Xを送る。- Aは、$Y_a$と$Y_b$のマルチシグアドレス$Y_{ab}$に
Yを送る。- 未署名トランザクション$TX_{ba}^X=CreateTx^X(X_{ab},X_a)$と、未署名トランザクション$TX_{ab}^Y=CreateTx^Y(Y_{ab},Y_b)$を生成する。※ ちなみに$CreateTx^{Chain}(sender, recipient)$とする。
- BがAにB分のアダプター署名 $\hat{\sigma_b}=EncSign(x_b,Y_a,TX_{ba}^X)$を送る。公証人鍵として$Y_a$を使う。
- Aは、$Y_a$で$\hat{\sigma_b}$を$EncVerify$して有効か確かめる。
- Aは、$\sigma_b=DecSig(y_a,\hat{\sigma_b})$して生の$\sigma_b$を復号し、A分の$\sigma_a$と組み合わせて署名した$TX_{ba}^X$をブロックチェーンXに書き込む。(Aは
Xをゲット)- Bは署名された$TX_{ba}^X$の復号された$\sigma_b$をブロックチェーンXから読み取って、$y_a=RecKey(\hat{\sigma_b},\sigma_b)$でA分の秘密鍵$y_a$を取得し、$TX_{ab}^Y$を署名してブロックチェーンYに書き込む。(Bは
Yをゲット)
ステップ6を完了した時点でAはXを手に入れ、BはY取得に必要なAの秘密鍵$y_a$の"材料"を同時に手に入れる。そこにスマートコントラクトや第三者による取次は発生しない。暗号プロトコルによって自動的にコインの所有権が交換される。
しかし、この仕組みをBitcoinとMoneroのアトミック・スワップにそのまま持ち込むことはできない。なぜなら、二つのコインは別の楕円曲線を採用しているからだ。つまり、BTC用公開鍵は$X_a=x_aG$なら、XMR用公開鍵は$Y_a=y_aH$となる。これは上のプロトコルの前提に反する。
では、どうするのか。
ここで使われるもう一つの技術が、異なる楕円曲線の離散対数の同等証明である。
異なる楕円曲線の離散対数の同等証明
- $DLProve(x)\rightarrow(\pi,X,Y)$:$X=xG$、$Y=xH$を証明する$\pi$を計算するアルゴリズム。
- $DLVerify(\pi, X, Y)\rightarrow{0, 1}$:証明$\pi$が正しければ1、間違って入れば0を返すアルゴリズム。
二つの公開鍵$X=xG$と$Y=yH$があるとして、$P$と$Q$の離散対数が等しい、つまり$x=y$であることを、$x$の所有者が$x$をバラさずに証明(ゼロ知識証明)することができるプロトコル。詳細はこちら
ざっくりとした流れ(異なる楕円曲線同士)
公証用の公開鍵をAは使う。
設定
- Aさん
- X用公開鍵: $X_a=x_aG$
- Y用公開鍵: $Y_a=y_aH$
- 公証用鍵: $X_a^y=y_aG$
- Bさん
- X用公開鍵: $X_b=x_bG$
- Y用公開鍵: $Y_b=y_bH$
手順の大きな変更点はステップ4で離散対数の同等証明を行うことである。
手順
- Bは、$X_a$と$X_b$のマルチシグアドレス$X_{ab}$に
Xを送る。- Aは、$Y_a$と$Y_b$のマルチシグアドレス$Y_{ab}$に
Yを送る。- 未署名トランザクション$TX_{ba}^X=CreateTx^X(X_{ab},X_a)$と、未署名トランザクション$TX_{ab}^Y=CreateTx^Y(Y_{ab},Y_b)$を生成する。※ $CreateTx^{Chain}(sender, recipient)$とする。
- Aは離散対数の同等証明で、$Y_a$と$X_a^y$の離散対数が等しいことをBに証明し、Bは検証する。
- BがAにB分のアダプター署名 $\hat{\sigma_b}=EncSign(x_b,X_a^y,TX_{ba}^X)$を送る。公証人鍵として$X_a^y$を使う。
- Aは、$X_a^y$で$\hat{\sigma_b}$を$EncVerify$して有効か確かめる。
- Aは、$\sigma_b=DecSig(y_a,\hat{\sigma_b})$して生の$\sigma_b$を取得し、A分の$\sigma_a$と組み合わせて署名した$TX_{ba}^X$をブロックチェーンXに書き込む。(Aは
Xをゲット)- Bは署名された$TX_{ba}^X$内の復号された$\sigma_b$をブロックチェーンXから読み取って、$y_a=RecKey(\hat{\sigma_b},\sigma_b)$でA分の秘密鍵$y_a$を取得し、$TX_{ab}^Y$を署名してブロックチェーンYに書き込む。(Bは
Yをゲット)
これで大まかなプロトコルが出来上がった。次に、参加者の一方が途中でプロトコルに従わなくなるケースを考える必要がある。
ビットコイン・スクリプトによるコントロール
Bitcoinの強力な機能に、ビットコイン・スクリプトがある。特に今回は、相手から一定期間応答がない場合、ロックされたコインが自分に戻ってくるように、OP_CHECKSEQUENCEVERIFYというオペコードを使いこなしてプロトコルを組み立てていく。

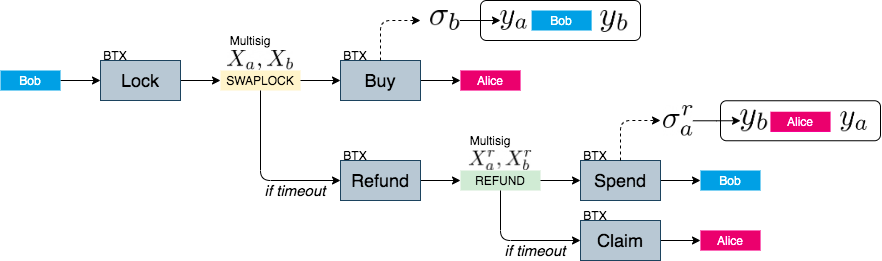
この図は今まで説明してきた流れを図示したものである。BがLockトランザクションでSWAPLOCKにBTCをロックする。AはBuyトランザクションで自分宛にロックされたBTCを引き出す。BはBuyトランザクション上で明らかになる$\sigma_b$からA分のXMR秘密鍵を復元し、BはXMRの所有権を手に入れる。
以下には、それぞれのスクリプトの詳細を記載する。
SWAPLOCK:資産ロック用scriptPubkey
OP_IF
OP_SHA256 <Hash(s)> OP_EQUALVERIFY
2 <X_a> <X_b> 2 OP_CHECKMULTISIG
OP_ELSE
<t_0> OP_CHECKSEQUENCEVERIFY OP_DROP
2 <X_a_refund> <X_b_refund> 2 OP_CHECKMULTISIG
OP_ENDIF
$X_{ab}$にロックされたBTCが引き出される先(Output)として指定されるscriptPubkey。
SWAPLOCKを解除するscriptSig
Buy:ロックされたBTCを手に入れる。
OP_0 <sig_a> <sig_b> <s> OP_TRUE <SWAPLOCK script>
Aが、$X_{ab}$から$X_a$に引き出す際に使われる。これにより、$\sigma_b$がBTCのブロックチェーンに晒されて、Bは$y_a$を復元することができる。また、sという値は、AがXMRを$Y_{ab}$にロックするのが確認され次第、BがAに渡す値である。この条件がないとXMRのロックなしにBTCがBuyされてしまう。
Refund:BUYスクリプトで一定期間署名されなかった場合。
OP_0 <sig_a_refund> <sig_b_refund> OP_FALSE <SWAPLOCK script>
AがBuyせずに$t_0$で指定した有効期限を過ぎた時、Bが$X_{ab}$から$X_b$に引き出す際に使われる。これにより、ロックされたBTCはREFUNDというscriptPubkeyにアウトプットされる。
Buyされなかったら
今までは参加者がプロトコルに従うことを期待していたが現実はそうはいかない。本記事で紹介するアトミック・スワップにもリカバリープランは組み込まれている。まず、上の流れでいつまでたってもAがBuyトランザクションを発行しない場合について説明する。
SWAPLOCKscriptPubkeyにロックされたままのBTCを、タイムアウト後にRefundトランザクションで救い出し、REFUNDscriptPubkeyにインプットさせているのが分かる。REFUNDから引き出すには、事前に共有した返金用の鍵による署名を必要とする。SpendトランザクションによってBがBTCを返金するときに晒される$\sigma_a^r$を使えばAはXMRの所有権を取り戻すのに必要な$y_b$を復元することができる。
返金用のアダプター署名
返金のためには逆のことをしなければならない。つまり、AはYを取り戻し、BはXを取り戻す。そのため、公証用の鍵はBも作る必要が出てくる。そして、公証用の鍵で返金用の鍵$X_b^r=x_b^rG$による署名を暗号化する。
REFUND:資産返金用scriptPubkey
OP_IF
2 <X_a_refund> <X_b_refund> 2 OP_CHECKMULTISIG
OP_ELSE
<t_1> OP_CHECKSEQUENCEVERIFY OP_DROP
<X_a> OP_CHECKSIG
OP_ENDIF
REFUNDを解除するscriptSig
Spend:ロックされたBTCとXMRを返金してもらう
OP_0 <sig_a_refund> <sig_b_refund> OP_TRUE <REFUND script>
BがREFUNDScriptPubkeyからBTCを引き出す際に使われる。$\sigma_a^{refund}$がBTCのブロックチェーンに晒されて、Bは$y_a$を復元することができる。よって、ロックされたBTCとXMRが全てBの物になる。
Spendされなかったら
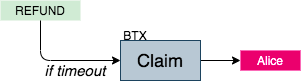
もちろんBがREFUNDscriptPubkeyから一定期間Spendしなかった際の救済措置も用意されている。Aは期限を迎えたREFUNDをインプットとするClaimトランザクションを彼女の署名だけで発行できる。
Claim:
<sig_a> OP_FALSE <REFUND script>
BがSpendせずに$t_1$で指定した有効期限を過ぎた時、AはBTCを手に入れることができる。
スクリプト全容
アダプター署名の仕組み
アダプター署名の元本から引っ張ってきた下図によると、8つのアルゴリズムで構成されている。

この図だと、$X$が署名鍵で$Y$が公証人鍵である。
この中でも$EncSign$に注目してみる。
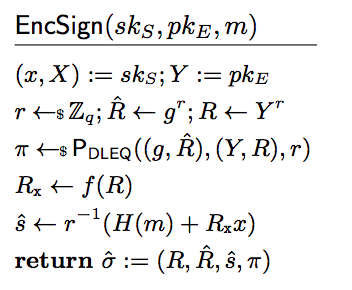
特に、二行目の$R\leftarrow Y^r$というのがミソだ。これは$secp256k1$の署名(上図だと$Sign$で表されている)の乱数部分を公証人の秘密鍵$y$を混ぜて$yr$とすることで、$EncSign$した本人でさえ生の署名を引き出せない秘匿性を実現している。
最後に
今回紹介したプロトコルは、何もBTCとXMRだけの交換に止まらず、BTCの代わりにビットコイン・スクリプトを扱えるBCHなどの通貨でも行える。また、離散対数同等証明を使えばXMR以外のどんな通貨でも(代表的な楕円曲線暗号を使っていれば)BTC系とのアトミック・スワップが可能になる。
残念ながら今の時点でこれら技術の実装は終わっておらず、本記事で紹介したアトミック・スワップを行えるサービスは完成していない。
しかし、アダプター署名による第三者の介在なしでチェーン上の権限を同時に入れ替える技術の応用力は計り知れない。アトミック・スワップはその一例に過ぎないのだ。
本記事はオリジナルの記事を砕いて説明しようとしたため、細部を端折っているところが多々ある。気になる人は元のリンクを辿っていただけると幸いだ。