【AtCoder】ABC301 D - Bitmask を二分探索問題と勘違いしていた
異端な解き方をしたようなのでメモ。
問題
考えたこと
Sの長さは最大60。
?の個数も最大60。
→単調増加の世界にできたら二分探索ができそう。
二分探索できるか検討してみる
例えばN=184、S="10?1??0?"の場合を考えてみる。
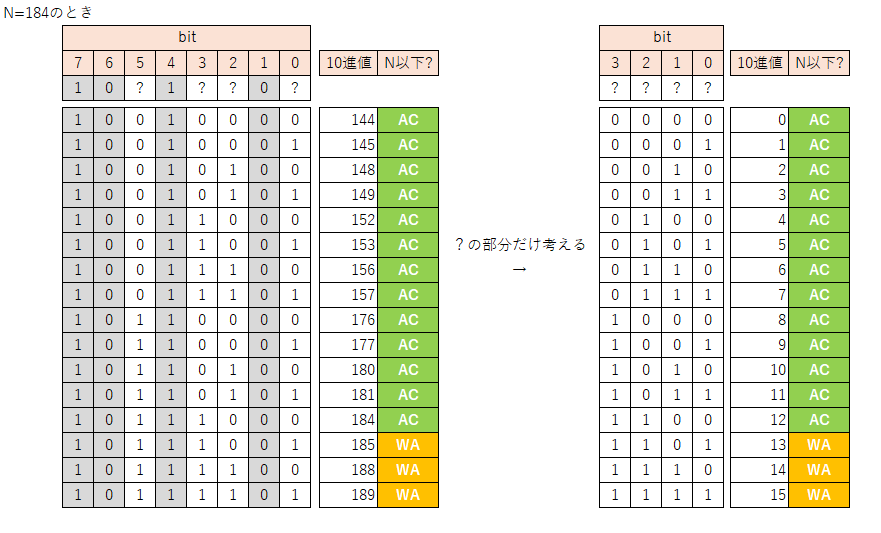
※図における「AC」と「WA」は公式解説動画の二分探索でよく使われている「正解ゾーン」と「不正解ゾーン」の意味。
?部分だけをbitとして持った64bit整数型で二分探索できそう。
ではどこから開始するか。
二分探索するためには絶対に正解であるACゾーンと、絶対に不正解であるWAゾーンを指定しなければならない。
ACゾーンの決定
?が全て0だったら最小値なのでACとなり得るか?
→ NO。前述の例の場合、Nが143などであればACではない。しかし全ての?が0でN以下にできないならばこの時点で-1を出力して終了すれば良い。この前提を踏まえた上であれば、ACゾーンを0から開始して良い。
WAゾーンの決定
これはシンプルに?を全て1にした場合の数+1と言える。前述の例で言えば190。この値は実現不可能なので正解になり得ない。
実装
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using vll = vector<ll>;
auto solve(string S, ll N) -> ll {
vll indicies;
for (ll i = S.size() - 1; i >= 0; --i) {
if (S[i] == '?') {
indicies.push_back(i);
}
}
auto to_ll = [&](ll m) {
string s(S);
for (ll i = 0; i < indicies.size(); ++i) {
s[indicies[i]] = (m >> i) & 1 ? '1' : '0';
}
ll n = 0;
ll v = 1;
for (ll i = s.size() - 1; i >= 0; --i) {
n += v * (s[i] - '0');
v *= 2;
}
return n;
};
if (N < to_ll(0)) {
return -1;
}
ll ac = 0;
ll wa = 1LL << indicies.size();
while (wa - ac > 1) {
ll wj = (wa + ac) / 2;
if (N >= to_ll(wj))
ac = wj;
else
wa = wj;
}
return to_ll(ac);
}
int main() {
string S;
cin >> S;
ll N;
cin >> N;
cout << solve(S, N) << endl;
return 0;
}