空いていたので、WebGL Advent Calendar 2018 5日目の記事にしました(WebGLというかGLSLですが...)。
12月1,2日に行われたTokyo Demo Fest 2018のGLSL Compoに「Refaction」という作品を提出しました。
実際に動いているものは以下から見ることができます(少し重いので注意してください)。
http://glslsandbox.com/e#50703.0
この作品では、真ん中のガラスっぽい直方体をレイマーチングで作成しています。
ここで使用している屈折表現について解説します。
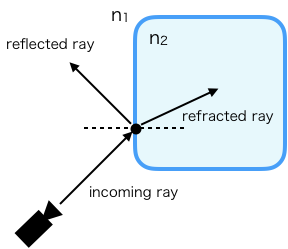
まず、カメラから通常のレイマーチングと同じようにオブジェクトの表面に到達するまでレイを飛ばします。表面に到達したら、GLSLの組み込み関数refectとrefractを使って反射方向と屈折方向を求めます。
反射方向はスペキュラー成分を求めるために使用し、屈折方向は背景をサンプリングすることに用います。
GLSLで実装すると以下のようになります。
float schlickFresnel(float ri, float cosine) {
float r0 = (1.0 - ri) / (1.0 + ri);
r0 = r0 * r0;
return r0 + (1.0 - r0) * pow(1.0 - cosine, 5.0);
}
float refractionIndex = 1.5;
vec3 lightDir = normalize(vec3(1.0, 1.0, 1.0));
vec3 lightColor = vec3(2.0);
vec3 substanceColor = vec3(0.90, 0.95, 1.0);
vec3 raymarch(vec3 ro, vec3 rd) {
vec3 p = ro;
for (int i = 0; i < 32; i++) {
float d = scene(p);
p += rd * d;
if (d < 0.01) {
vec3 n = normal(p);
vec3 reflected = reflect(rd, n);
float f = schlickFresnel(refractionIndex, max(0.0, dot(-rd, n)));
vec3 spec = f * lightColor * pow(max(0.0, dot(reflected, lightDir)), 4.0);
vec3 refracted = refract(rd, n, 1.0 / refractionIndex);
return spec + substanceColor * background(p, refracted);
}
}
return background(ro, rd);
}
スペキュラー成分はPhongシェーディングで計算しています。Schlickの近似式で求めたフレネル係数をかけることで、浅い角度から見たときに光がより反射するようになります。
オブジェクトと直方体を描画するとそれぞれ次のようになります。


ここまででもそれなりに雰囲気がでますが、レイの射出時の再屈折をさらに考慮してみたいと思います。
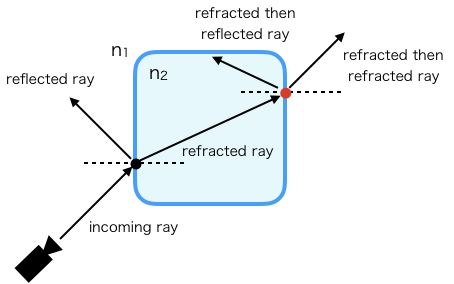
再屈折を考慮する場合には、屈折したレイが背面のどこから射出するかを知る必要があります。これは、屈折したレイの先にある十分に遠くの地点からそのレイの反対向きにレイを飛ばすことで実現します。
再屈折する位置がわかったので、ここでもう一度refract関数を用いて射出方向を計算します。射出方向が求まれば、そこから背景をサンプリングできます。注意しないといけないのは、入射角がある値を超えると全反射が起きて屈折しないことがある点です。その場合にはrefract関数はvec3(0.0)を返します。ここからレイがオブジェクトから射出するまで同じ処理を繰り返してもいいのですが、パフォーマンス的なことも考えて今回は反射方向で背景をサンプルすることにします。
これをGLSLで実装すると以下のようになり、2回レイマーチングを行うようになります。
vec3 raymarch(vec3 ro, vec3 rd) {
vec3 p = ro;
for (int i = 0; i < 32; i++) {
float d = scene(p);
p += rd * d;
if (d < 0.01) {
vec3 n = normal(p);
vec3 reflected = reflect(rd, n);
float f = schlickFresnel(refractionIndex, max(0.0, dot(-rd, n)));
vec3 spec = f * lightColor * pow(max(0.0, dot(reflected, lightDir)), 4.0);
vec3 refracted = refract(rd, n, 1.0 / refractionIndex);
vec3 op = p + refracted * 100.0;
for (int j = 0; j < 32; j++) {
float d = scene(op);
op += -refracted * d;
if (d < 0.01) {
vec3 n2 = normal(op);
vec3 refracted2 = refract(refracted, -n2, refractionIndex);
if (length(refracted2) > 0.01) {
return spec + substanceColor * background(op, refracted2);
} else {
vec3 reflected2 = reflect(refracted, -n2);
return spec + substanceColor * background(op, reflected2);
}
}
}
}
}
return background(ro, rd);
}
このようにしたときの球と直方体は以下のようになります。入射位置での屈折方向で背景をサンプリングしたときと比べると、特に直方体での背面の角の部分がリアルになっている感じがします。


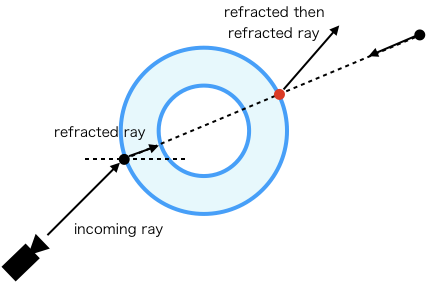
なお、この方法は凸面体ならば(たぶん)上手くいきますが、凹面体では上手くいかないです。
例えばトーラスで同じアルゴリズムを適用すると以下のようになり、正確に再現できていません。

今回のサンプルは以下から確認できます。scene関数から描画するオブジェクトの形状を変更できます。
また、#define MULTI_REFRACTIONをコメントアウトすることで入射位置での屈折方向で背景をサンプリングするようになります。
http://glslsandbox.com/e#50748.0