レイと点の最短距離をベクトル計算で求める

レイと点の最短距離をベクトル計算で求める方法です。

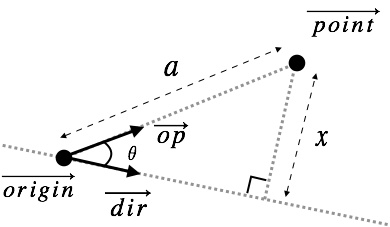
レイは以下の図のように位置ベクトル$\vec{origin}$と方向ベクトル$\vec{dir}$で表し、点は位置ベクトル$\vec{point}$で表します。求めたいのはレイとベクトルの最短距離$x$です。以下の計算では方向ベクトル$\vec{dir}$は正規化されているとします。

$\vec{point}$と$\vec{origin}$の距離を$a$とし、$\vec{origin}$から$\vec{point}$へ向かうベクトル$\vec{op}$と$\vec{dir}$がなす角を$\theta$とすると余弦の定義から以下のような方程式が成り立ちます。

sin\theta = \frac{x}{a}

これを$x$について解くと以下のようになり、$a$と$sin\theta$を求めれば$x$を求めることができることがわかります。

x = asin\theta

aは位置ベクトル間の距離で以下のように求まります。

\vec{op} = \vec{point} - \vec{origin} \\
a = \sqrt{dot(\vec{op}, \vec{op})}

$sin\theta$は$sin\theta^2 + cos\theta^2 = 1$より以下のように求まります。

\vec{op} = normalize(\vec{point} - \vec{origin}) \\
cos\theta = dot(\vec{dir}, \vec{op}) \\
sin\theta = \sqrt{1 - cos^2\theta}

この計算をプログラムで書くと以下のようになります。プログラムはJavaScriptで、ベクトルクラスにはp5.jsのp5.Vectorを使っています。

JavaScript

function calcDistance(origin, dir, point) {
  const pointToOrigin = p5.Vector.sub(point, origin);
  const pointToOriginLength = pointToOrigin.mag();
  pointToOrigin.normalize();
  const cosTheta = p5.Vector.dot(dir, pointToOrigin);
  return pointToOriginLength * sqrt(1 - cosTheta * cosTheta);
}

以下の画像ではレイと点の最短距離を求めて、距離で色付けしています。
https://www.openprocessing.org/sketch/546990