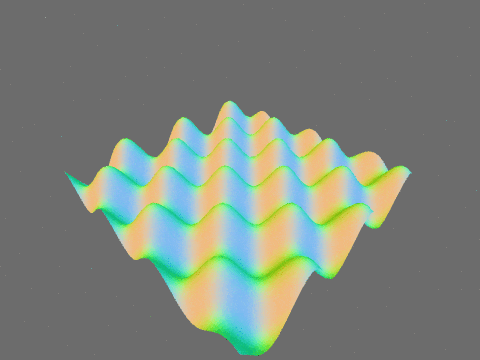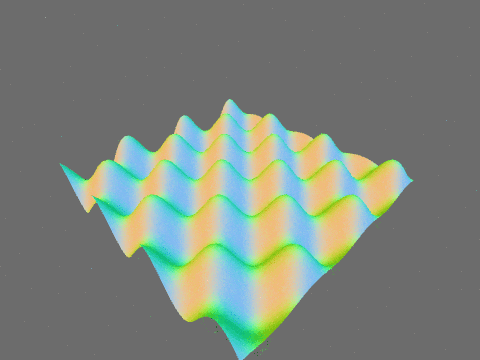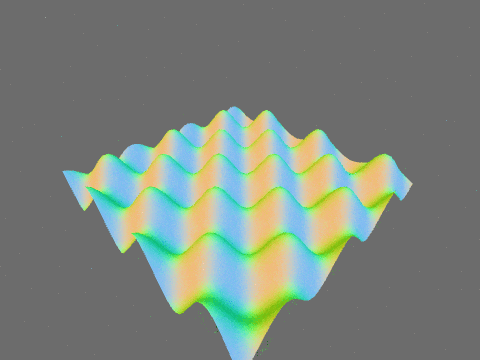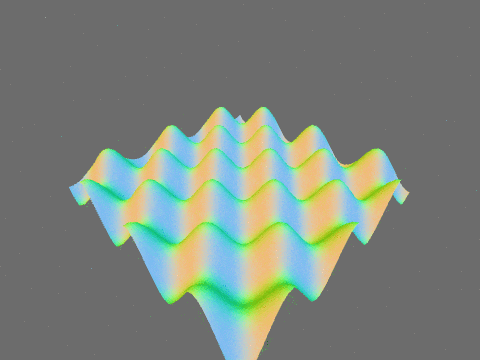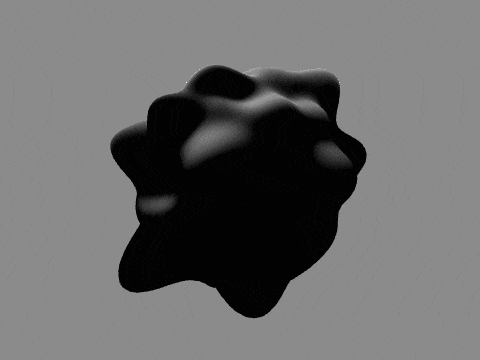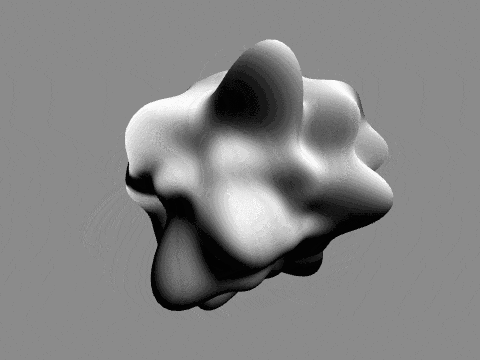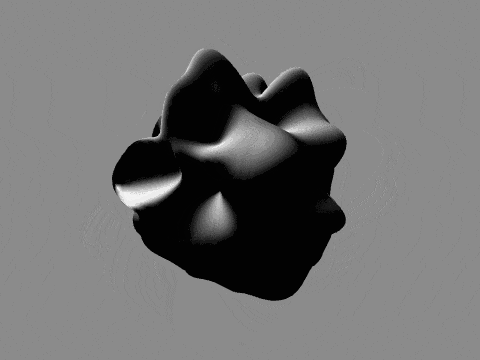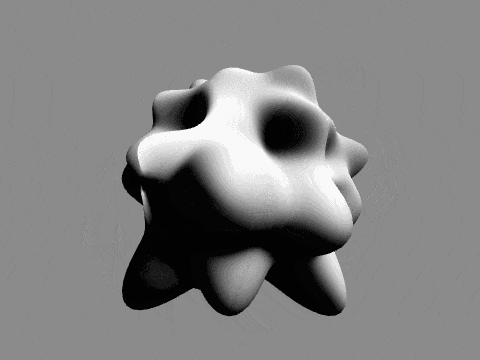【Unity】頂点シェーダーで頂点を変形した後に法線を再計算する

以前に頂点シェーダーで頂点を変形した後にジオメトリシェーダーで法線を再計算する方法について書きました。
【Unity】頂点シェーダーで頂点を変形した後にジオメトリシェーダーで法線を再計算する - Qiita

この方法では三角形プリミティブの法線がすべて同じになってしまうため、フラットシェーディングになってしまうという欠点がありました。

もっといい方法がないかなと思っていたところ、GPU Gemsに頂点シェーダーで法線の再計算を行う方法について書いてあったので試してみました。
GPU Gems | NVIDIA Developer

記事中ではヤコビ行列を用いて変形後の接線と従法線を計算していますが、ヤコビ行列を求めるにはあらかじめ変形操作を数式で表し、さらにその一階微分を求める必要があるため、めんどくさいので今回は採用しません。

その代わりに、変形前の頂点に対して接線と従法線方向に近傍点を取り、その近傍点も同様に変形させてから、頂点と変形させた近傍点への方向でクロス積をとることにより法線を求め直しています。

イメージとしては頂点周辺に小さい三角形を作り、その三角形で以前の記事で行ったような頂点の計算をしているような感じです。

以下は以前の記事と同様にサイン波で平面を変形させたものです。法線が滑らかに変化していることがわかります。

SineWave.shader

Shader "Sample/SineWave"
{
    SubShader
    {
        Tags { "RenderType"="Opaque" }

        Pass
        {
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag

            #include "UnityCG.cginc"

            float _Flat;

            struct appdata
            {
                float4 pos : POSITION;
                float3 normal : NORMAL;
                float3 tangent: TANGENT;
            };

            struct v2f
            {
                float4 pos : SV_POSITION;
                float3 normal : TEXCOORD1;
            };

            float3 modify(float3 pos) {
               return float3(pos.x, pos.y + sin(pos.x * 2.0 + _Time.x * 5.0) * cos(pos.z * 2.0 + _Time.x * 10.0), pos.z);
            }

            v2f vert (appdata v)
            {
                v2f o;
                float3 pos = modify(v.pos);
                float3 tangent = v.tangent;
                float3 binormal = normalize(cross(v.normal, tangent));

                float delta = 0.05;
                float3 posT = modify(v.pos + tangent * delta);
                float3 posB = modify(v.pos + binormal * delta);

                float3 modifiedTangent = posT - pos;
                float3 modifiedBinormal = posB - pos;
                o.normal = normalize(cross(modifiedTangent, modifiedBinormal));

                o.pos = UnityObjectToClipPos(pos);


                return o;
            }

            fixed4 frag (v2f i) : SV_Target
            {
                return fixed4(i.normal * 0.5 + 0.5, 1.0);
            }
            ENDCG
        }
    }
}

これまた以前の記事と同様に球をノイズで変形させ、ライティングしたものです。

Light.shader

Shader "Sample/Light"
{
    Properties
    {
        _Color ("_Color", Color) = (1, 1, 1, 1)
        _NoiseScale ("_NoiseScale", Range(0, 5)) = 1
        _NoiseAmount ("_NoiseAmount", Range(0, 10)) = 3
        _NoiseTime ("_NoiseTime", Range(0, 5)) = 1
    }
    SubShader
    {
        Tags { "LightMode"="ForwardBase" "RenderType"="Opaque" }

        Pass
        {
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag

            #include "UnityCG.cginc"
            #include "UnityLightingCommon.cginc"
            #include "ProceduralNoise/SimplexNoise4D.cginc"

            fixed4 _Color;
            float _Flat;
            float _NoiseScale;
            float _NoiseAmount;
            float _NoiseTime;

            struct appdata
            {
                float4 pos : POSITION;
                float3 normal : NORMAL;
                float3 tangent : TANGENT;
            };

            struct v2f
            {
                float4 pos : SV_POSITION;
                float3 normal : TEXCOORD1;
                fixed4 diff : COLOR0;
            };

            float3 modify(float3 pos) {
                float3 normal = normalize(pos);
                return pos + normal * (simplexNoise(float4(pos.xyz * _NoiseScale, _Time.x * _NoiseTime)) * 0.5 + 0.5) * _NoiseAmount;
            }

            v2f vert (appdata v)
            {
                v2f o;
                float3 pos = modify(v.pos);
                float3 tangent = v.tangent;
                float3 binormal = normalize(cross(v.normal, tangent));

                float delta = 0.05;
                float3 posT = modify(v.pos + tangent * delta);
                float3 posB = modify(v.pos + binormal * delta);

                float3 modifiedTangent = posT - pos;
                float3 modifiedBinormal = posB - pos;
                o.normal = normalize(cross(modifiedTangent, modifiedBinormal));

                o.pos = UnityObjectToClipPos(pos);
                o.diff = max(0, dot(o.normal, _WorldSpaceLightPos0.xyz)) * _LightColor0;

                return o;
            }

            fixed4 frag (v2f i) : SV_Target
            {
                return _Color * i.diff;
            }
            ENDCG
        }
    }
}