GLSLでIFSシェルピンスキーのカーペット

最近、GLSLでIFSフラクタルを描く勉強しています。

手始めにMneger Spongeと思ったのですが、3Dよりも2Dのほうが簡単だろうということでMenger Spongeの2D版といった感じのシェルペンスキーのカーペットを考えてみました。

実際にやろうするとどのように空間を操作するかが難しく、半日ぐらい悩んだので備忘録として記事にしました。

自分で考えた方法とiq氏がこちらの記事でMenger Spongeについて解説している方法を参考にしたものの二通りを紹介します。
どちらを使用しても結果は同じになるはずです(たぶん)。

自分で考えた方法

ブーリアン演算で繰り返し差を取ることでシェルピンスキーのカーペットを作成します。
実際のコードと動くものはこちらで見られます。

float sierpinskiCarpet(vec2 p) {
    float s = 1.0;
    float f  = 1.0 / 3.0;
    float d = sdBox(p, vec2(s));
    for (int i = 0; i < 4; i++) {
        d = max(d, -sdBox(p, vec2(f)) / s);
        p = abs(p);
        p -= f;
        p = abs(p);
        p -= f;
        p *= 3.0;
        s *= 3.0;   
    }
    return d;   
}

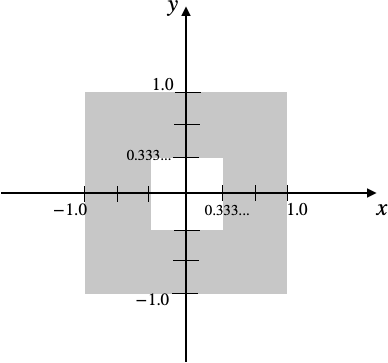
まず、float d = sdBox(p, vec2(s));を正方形を描きます。
そこからd = max(d, -sdBox(p, vec2(f)) / s);で論理差を取り、真ん中に穴を開けます。

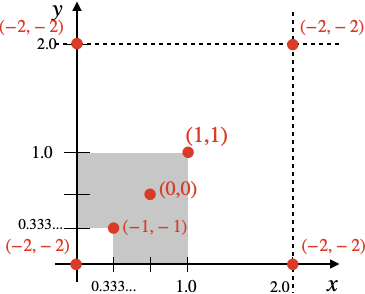
次に周囲8近傍についても穴を開ける必要がありますが、X軸、Y軸それぞれについて対称なのでabs(p);で空間を折りたたみます。これにより$x \geqq 0$かつ$y \geqq 0$の座標だけを考えればよくなります。

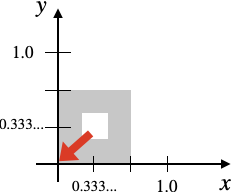
折りたたんだものを見ると、X軸、Y軸それぞれについて$(x, y)=(0.333..., 0.333...)$で（左下を無視すれば）対称になので、p -= f;で$(x, y)=(0.333..., 0.333...)$を原点に移動させてからp = abs(p);で空間をもう一度折りたたみます。

折りたたんだものをp -= f;で穴が真ん中になるように座標を移動させます。

その結果、以下のようになり、p *= 3.0;することで最初の画像と同じ状態に戻るので、同じ操作を繰り返し穴を開けていくことができます。

iq氏のMenger Spongeを参考にした方法

ブーリアン演算で繰り返し積を取ることでシェルピンスキーのカーペットを作成します。
コードと実際に動くものはこちらでみられます。

float sdCross(vec2 p) {
    p = abs(p);
    return min(p.x, p.y) - 1.0;
}

float sierpinskiCarpet(vec2 p) {
    float d = sdBox(p, vec2(1.0));

    float s = 1.0;
    for (int i = 0; i < 4; i++) {
        vec2 a = mod(p * s, 2.0) - 1.0;
        vec2 r = 1.0 - 3.0 * abs(a);
        s *= 3.0;
        float c = sdCross(r) / s;
        d = max(d, c);
    }
    return d;
}

最初にfloat d = sdBox(p, vec2(1.0));で四角形を描くのは先に述べた手法と同じです。

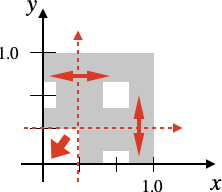
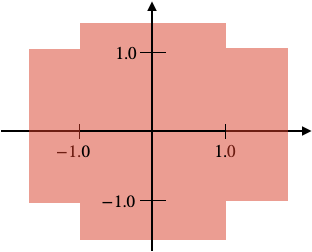
vec2 a = mod(p * s, 2.0) - 1.0;で座標を操作をすると赤で示したようになります。

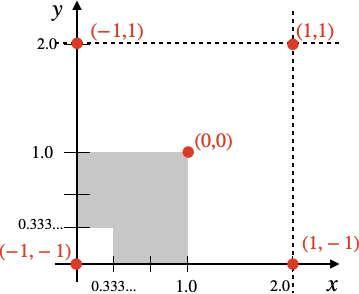
さらにvec2 r = 1.0 - 3.0 * abs(a);で座標は次のようになります。

float c = sdCross(r) / s;は以下のような形となっており、d = max(d, c);で論理積を取ることで穴以外の部分を残すことができます。

　余談

iq氏のMenger Spongeの記事は大変参考になるのですが、最初のコードでは論理差を取るのに、繰り返しが導入されてからは論理積をとるようになるので記事を読み進める上で注意が必要です。