Excel の LAMBDA 関数を試す (2)

以前 LAMBDA の入門記事を書きましたが、 @ytaki0801 さんの指摘で LAMBDA にまだ知らない機能があることを知ったので（無知の知）、補足的な記事を書きました。

• 前の記事：Excel の LAMBDA 関数（ベータ版）を試す | Qiita

以下ではなるべくラムダ計算の専門用語を使わずに不動点コンビネータを解説しています。不適切な記述があれば、ご指摘いただけると幸いです。

複雑奇怪な数式

前回の記事で「 LAMBDA 内でローカル関数を定義しても 再帰的 には使えない」と書きました。それ自体は間違っていないのですが、公式ブログにしっかり対応例が載っていました。以下の式を入力すると、A1 セルの値を参照して、その階乗を返してくれます。ただ一見して仕組みが理解できない。。。¹

何これ？

=LET(
     Z, LAMBDA(f, LET(g, LAMBDA(x, f(LAMBDA(v, LET(xx, x(x), xx(v) )))), g(g))),
     myfact, Z(LAMBDA(myfact, LAMBDA(x, IF(x=0,1,x*myfact(x-1))))),
     myfact(A1)
)

• 参考：LAMBDA: The ultimate Excel worksheet function | Microsoft Research Blog

この記事ではこの数式を読み解くことを通じて、 LAMBDA を用いてローカルに再帰関数を定義する方法を勉強したいと思います。

数式の前処理

まずこの数式を正しく理解するうえで重要なのは、3行目左辺の myfact と右辺の myfact が異なるものだ と認識することです。実際、次のように別々の名前に置き換えても問題なく動きます。

誠実な数式

=LET(
     Z, LAMBDA(f, LET(g, LAMBDA(x, f(LAMBDA(v, LET(xx, x(x), xx(v) )))), g(g))),
     MYFACT, Z(LAMBDA(RECUR, LAMBDA(x, IF(x=0,1,x*RECUR(x-1))))),
     MYFACT(A1)
)

つまり、Z で囲まれた　Z(LAMBDA(myfact, LAMBDA(x, IF(x=0,1,x*myfact(x-1))))) の部分が再帰関数になっているということですね。3行目ではこうしてできた再帰関数を、新たに myfact という変数に上書きしていたにすぎません。ミスリーディングなので注意しましょう。

というわけで、関数 Z がこの数式の核であり、これを理解することで数式全体が理解できるようになります。

顧客が本当に欲しかったもの

素朴に再帰を書こうとすると、まあ以下のようになると思いますが、これでは名前解決に失敗してしまいます。右辺を左辺に代入するわけですが、右辺に定義前の myfact が出てきているので、そこでエラーになるという寸法です。このような自己参照はできません。

シンプルな数式（動かない）

=LET(
    myfact, LAMBDA(x, IF(x=0, 1, x*myfact(x-1))),
    myfact(A5)
)
// >>> #NAME?

そこで、このような等式を用いる素朴な方法とは別の方法で、再帰関数を定義する必要があります。

不動点コンビネータ

名前を用いた自己参照ができないとき、不動点コンビネータを用いた再帰関数の定義が有効です。

簡単に言うと、（定数関数を除いた）ふつうの関数は何かしら変数を持っているわけですが、その変数部分に自分自身が代入されるようなものを再帰関数と言います。不動点コンビネータを用いると、与えた関数を再帰関数にして返してくれます。

上で挙げた２つの数式を比較してみましょう。「動くほうの式」をよく見ると、右辺に「動かないほうの式」が丸ごと埋め込まれているように見えますね。LAMBDA 内で自己参照的な定義をして、それを不動点コンビネータ Z に渡しています。

// 動くほうの式
MYFUNC, Z(LAMBDA(RECUR, LAMBDA(x, IF(x=0, 1, x*RECUR(x-1))))),
// 動かないほうの式
                 RECUR, LAMBDA(x, IF(x=0, 1, x*RECUR(x-1))),

Y コンビネータ

最も有名な不動点コンビネータ（と言われている） Y コンビネータを考えてみましょう。後ほど見るように、Excel では Y コンビネータはそのままでは動かないのですが、形がシンプルなので、不動点コンビネータを理解するには適しています。

Y コンビネータはラムダ記法で Y = (λf.(λx.f(xx))(λx.f(xx))) と書くらしいですが、これをエクセル記法で書くと LAMBDA(f, LAMBDA(x, f(x(x))(LAMBDA(x, f(x(x)))) となります。

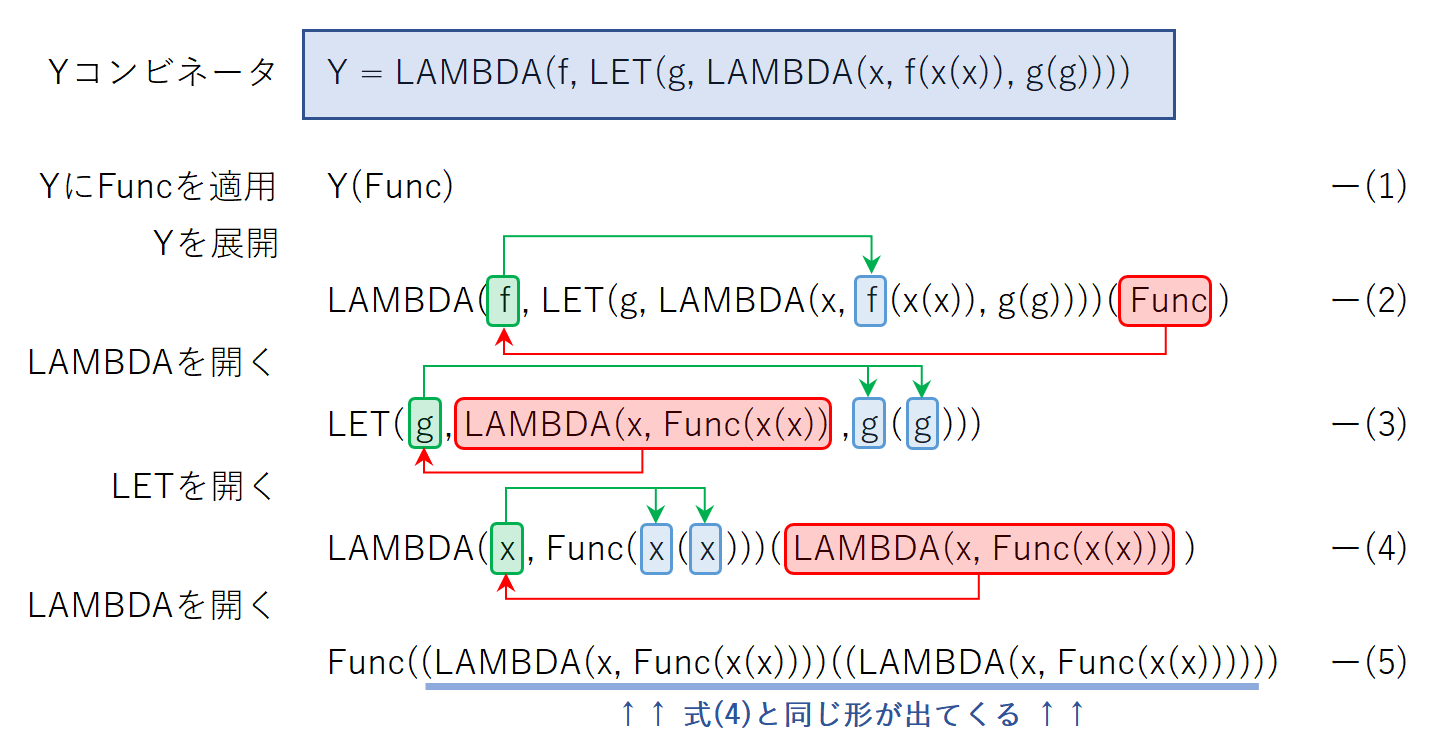
LET を用いてシンプルに書き直すと LAMBDA(f, LET(g, LAMBDA(x, f(x(x)), g(g)))) となります。公式の例に近い形なので、とりあえずこちらを採用しましょう。

Yコンビネータによる再帰関数（動かない）

=LET(
     Y, LAMBDA(f, LET(g, LAMBDA(x, f(x(x)), g(g)))),
     MYFACT, Y(LAMBDA(RECUR, LAMBDA(x, IF(x=0,1,x*RECUR(x-1))))),
     MYFACT(A1)
)

理屈としては、x(x) と g(g) のような関数を関数に適用する部品が互いに代入し合うことで、フラクタルのように延々と同じ構造が出現するようになっていて、そこに外部から再帰させたい関数 f を噛ませることで、再帰関数を実現しているわけです。

上のような具合で Z(Func) = Func(Z(Func)) = Func(Func(Z(Func))) = ... と再帰していきます。

ただ実用的な再帰関数というのは、どこかで収束する必要があります。収束に関わる条件（階乗なら n-1 の部分）は与える関数が負うにしても、不動点コンビネータ自体は「関数から再帰関数を生み出す」だけの抽象的な定義でしかありませんから、不動点コンビネータが与えられた段階で、とりあえず展開しきろうとすると、永遠に展開が終わりません（ということは、値渡しであるということ）。ですので、言語のほうで展開を猶予するような機構にするか、さもなくば不動点コンビネータを工夫して、外部から実際に計算に使う値を与えないと展開が進まないようなストッパー機構をつけておく必要があります。

Z コンビネータ

Y コンビネータにストッパー機構をつけたものが Z コンビネータです。公式が Z と名付けているのは、実はこの Z コンビネータを念頭に置いているのでした。

その形を Y コンビネータと比べてみましょう。f(x(x)) の部分が何やら複雑な形になっています。

YコンビネータとZコンビネータ

Y, LAMBDA(f, LET(g, LAMBDA(x, f(x(x)), g(g)))),
Z, LAMBDA(f, LET(g, LAMBDA(x, f(LAMBDA(v, LET(xx, x(x), xx(v) )))), g(g))),

ここで xx という文字列は x と関係があるように見えますが、これはミスリーディングで、特に xx である必然性はないので、とりあえず w と置き換えます。

YコンビネータとZコンビネータ’

Y, LAMBDA(f, LET(g, LAMBDA(x, f(x(x)), g(g)))),
Z, LAMBDA(f, LET(g, LAMBDA(x, f(LAMBDA(v, LET(w, x(x), w(v) )))), g(g))),

先ほどと同じような変形をしてみると、単純な再帰にはなっておらず LAMBDA v LET w が間に残ることが分かります。

上のような具合で Z(Func) = Func(LAMBDA(v, LET(w, Z(Func), w(v)))) と変形されます。純粋な再帰の形ではなく、この段階では LAMBDA や LET が残っているため、これ以上の展開が猶予されています。

こうして完成した再帰関数 Z(Func) に RECUR と名前を付け、実際に値 num を代入してみましょう。Func と RECUR の引数は同数と考えられますから（この場合１個を想定）、num の代入先はすべて引数に由来するものであり、Func をすり抜けて引数に適用して良いということになります（実際には具体的に Func の形が展開されるわけですが）。そうすると雪崩式に LAMBDA と LET が整理され、はじめて純粋な再帰の形が発生します。

// Z(Func) に RECUR と命名する
RECUR      = Func(LAMBDA(v, LET(w, RECUR, w(v))))

// RECUR に値 num を代入する
RECUR(num) = Func(LAMBDA(v, LET(w, RECUR, w(v))))(num)
           = Func(LAMBDA(v, LET(w, RECUR, w(v)))(num))
           = Func(LET(w, RECUR, w(num)))
           = Func(RECUR(num))

というわけで、Z コンビネータを用いると、値を代入したときにはじめて純粋な再帰形になる再帰関数が得られることになります。

再帰を収束させる

いくらストッパーを作っていい感じに計算が進むようになっても、計算が終わらないのでは（実用的に）意味がありません。不動点コンビネータに渡す関数に仕掛けをして、計算が収束するようにしておく必要があります。

公式では以下のような使い方をしています。

Z(LAMBDA(RECUR, LAMBDA(x, IF(x=0,1,x*RECUR(x-1)))))

高校数学よろしく漸化式で書くと、以下のような数式ですね。n=0 で再帰がストップするようになっています（自然数以外を渡すと #NUM! を吐いて死にます）。

func(x) = x * func(x-1)     ( x ≠ 0 )
        = 1                 ( x = 0 )

応用例

あとで追記します。

おまけ

最後に、Wikipedia「不動点コンビネータ」の記事から印象的な言葉を引用しておきます。

不動点コンビネータにより、第一級関数をサポートしているプログラミング言語において、明示的に再帰を書かずに再帰を実現する為に用いる事ができる。なお、一般にそういった言語では普通に再帰が使えるので、プログラミングにおいてはパズル的なテクニック以上の意味は無い。

せめてもう少し分かりやすいシンタックスシュガーを作ってほしいですね。というか素直に名前の登録使って。

参考

• YコンビネータとZコンビネータ（Ruby） | Camera Obscura

1. 1行目の rem, "https://en.wikipedia.org/wiki/Fixed-point_combinator#Strict_fixed-point_combinator" は数式上は何の意味も持たない部分なので、ここでは省略しますが、これはWikipedia「不動点コンビネータ」の記事へのリンクになっています。 ↩