(ニューラルネットワークの話ですが機械学習はしません)
はじめに
今年は機械学習、特に deep learning が爆発的に広まった年でした。"ほげほげNN
"とか"ふがふがNet"に関わる機会が増えた人も多いと思います。
アルゴリズムを学習させるような試みもあり、Turing machine freak の私としてはやはり気になることが出てきます。
「ニューラルネットワークはチューリング完全なのだろうか?」
この程度の問題であれば、論文を探して読んで理解するよりも自分で考えるほうが早いし、なにより面白いので自分で考えてみます。(参考文献は)ないです。
結論を先にいうと、「再帰(と分岐)の機構を導入したらチューリング完全になった」でした。
"Neural" とか "Network" とかどうでもいい
私は(自分を含め)人間があんまり好きじゃないので、神経とか脳とか言われても困ります。
neural とかいうけれど、やっていることは線形結合と活性化関数の合成です。
network とかいうけれど、やっていることは関数の合成の繰り返しを図にしただけです。
そう、ニューラルネットワークというのは、線型結合と活性化関数の合成の繰り返しでしかないのです。
この関数の合成の繰り返しで、目的となる関数を表現ないし近似するわけです。まさに這い寄る混沌(漸近するカオス系)ですね。
活性化関数
線形結合だけではいくら合成しても線形結合しか表現出来ません。そこで活性化関数の出番となるわけです。
ではどんな活性化関数を使えば良いのでしょう?
元も子もない話をすると、目的の関数を活性化関数にしてしまえば良いのです。
しかしこれではダメで、「目的の関数を知らなくても、パラメータ(線形結合の係数)をいじっていくうちに目的の関数に近づく」というNNの良さが失われてしまっています。
逆に言えば、我々の目指すべきは「線型結合の係数をいじるだけで任意のプログラムが表現出来るネットワーク」だということになります。
つまり、活性化関数は予め決めた有限個のものを使うという縛りが発生します。
ReLU
例えば活性化関数として ReLU (Rectified Linear Unit) (と恒等写像)を使う場合を考えてみます。
$$ \text{ReLU}(x) = max\{0, x\} = \begin{cases} x & \text{if } x \geq 0 \\ 0 & \text{otherwise} \end{cases} $$
実は、これは活性化関数として絶対値 $f(x) = |x|$ (と恒等写像) を採用することと同等になります。次の式によって、ReLUと絶対値関数はお互いを表現出来るからです:
$$\begin{eqnarray*}
\text{ReLU}(x) &=& \frac{1}{2}|x| + \frac{1}{2}x \\
|x| &=& \text{ReLU}(x) + \text{ReLU}(-x)
\end{eqnarray*}$$
つまり、ReLUを活性化関数として採用した場合、表せる関数は絶対値と線型結合の組み合わせで表現出来る関数、ということになります。
台形関数(造語です)
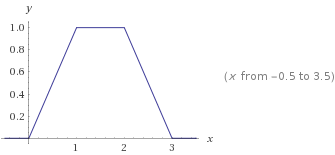
もうちょっと突き詰めていくと、下記のような「台形関数」を作ることが出来ることがわかります:
$$ f(x) = ReLU(x) - ReLU(x-1) - ReLU(x-2) + ReLU(x-3) $$
パラメータ(上の関数だと-1,-2,-3 や ReLU の係数) をいじってやることでいろんな「幅」や「高さ」の台形関数を作ることが出来て、しかもそれらの線形結合も出来るため、かなりいろんな関数を近似することが出来ます。
今回はReLUをベースに作ったので微分可能でない点がありますが、例えば sigmoid 等の$C^\infty$な関数をベースに同じことをやると、いわゆる Bump function が出来ます。
Bump function が作れて、それらの線形結合が出来るのだから、大抵の関数は近似できることがわかります。
(「大抵」というのは「有界でサポートがコンパクトで一様連続」のはず)
但しこれによる近似をする場合、グラフのノードの個数をどんどん増やしていく必要があります。我々はネットワークの形を変えるつもりはありません。
自乗関数(2乗する関数)
あまり聞かない話ですが、活性化関数として $f(x)=x^2$ (と恒等写像)を採用すると、なんと全ての多項式が表現出来てしまいます。
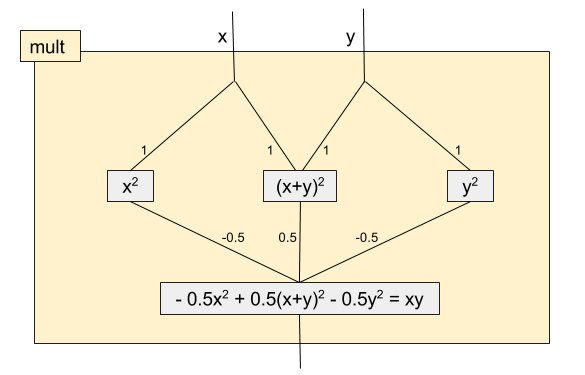
$$xy = \frac{1}{2}(x+y)^2 - \frac{1}{2}x^2 - \frac{1}{2}y^2$$
上の式により、2つの変数の掛け算が「2乗する」関数と「線形結合する」関数の合成によって表現出来ることが分かります。
足し算は線形結合で表現できるため、「足し算」と「掛け算」が出来ます。よって全ての多項式が表現出来てしまうのです。
因みに、このネットワークを図にするとこんな感じです:
チューリングマシンを作るために
ここまで、「こんな活性化関数を使うとこんな関数が表現出来る」という話を続けてきましたが、キリがないのでチューリングマシンを作ろうとしてみます。
が、すぐに壁にぶち当たります。
分岐と再帰(or繰り返し)が必要です。さあどうする。
分岐
安直に考えると(?)、ヘヴィサイド関数を使えば良さそうです。
$$H_1(x) = \begin{cases} 1 & x \geq 0 \\ 0 & \text{otherwise} \end{cases}$$
これと(pointwiseな)掛け算をしてやることで、 $x \geq 0$ のときは $f(x)$、そうでなければ $0$ といったことが出来るようになります。
もうちょっと工夫して、
$$H_1(x) \cdot f(x) + (1-H_1(x)) \cdot g(x)$$
とすれば、$x \geq 0$ のときは $f(x)$、そうでなければ $g(x)$ になりますね。
掛け算をしたいので、自乗関数も活性化関数として採用することになります。
再帰
これは色々方法がありそうです。私の思いつく限りでは、
- 「再帰ノード」みたいなのを導入する
- 末尾再帰にして、RNNみたいな感じで(加算)無限個のノードを用意する
- 高階関数を扱えるようにする
といった方法が挙げられます。
無限個のノードを用意する場合、無限個のノードから出て来る無限個の出力をどう扱うか、という問題が出てきてめんどいです。
高階関数を扱えるようにすればラムダ計算が出来るので全ての話が終わりますが、ネットワークとして表現する方法は分かりません。
そのため、「再帰ノード」みたいなのを導入することにします。部分グラフに名前をつけておいて、それを参照するイメージ。
Fact, we build
チューリングマシンの前に、分岐と再帰が本当に出来てるか確かめましょう。階乗関数を作ってみます。
まずは式から作ります:
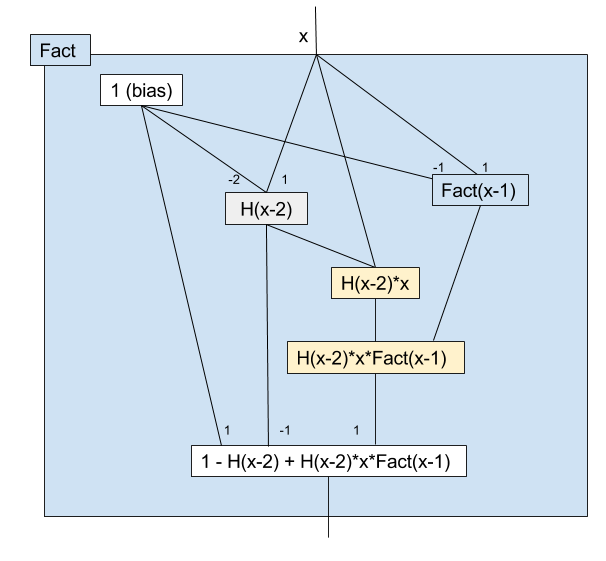
$$ \text{Fact}(x) = 1-H_1(x-2)+H_1(x-2)\cdot x \cdot \text{Fact}(x-1)$$
$1-H_1(x-2)$ が再帰の終わりの部分で、$x \lt 2$ の時ここは $1$ になり、$x \geq 2$ の時ここは$0$になります。
$H_1(x-2)\cdot x \cdot \text{Fact}(x-1)$ が再帰の途中の部分で、$x \lt 2$ の時ここは 0 になり、$x \geq 2$ の時ここは $x \cdot \text{Fact}(x-1)$ になります。まさに階乗ですね。
このネットワークを図にするとこんな感じです:
(黄色のノードはmultの部分グラフを省略しているものと考えて下さい)
しかしこのネットワークには問題があります。素直に評価しようとすると、再帰が終わらないのです。
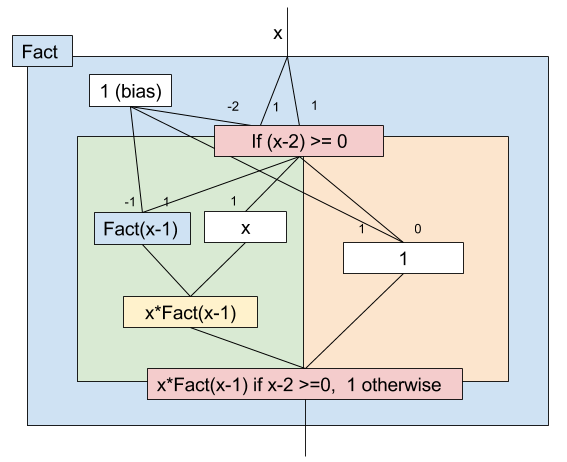
処理系が遅延評価すればいい、という話もあると思いますが、ネットワークが難解なのもあるので、ifに相当する機構を用意しようと思います。
図にするとこんな感じです:
数式的には単純に if を使って、
$$\text{Fact}(x) = \begin{cases} x \cdot \text{Fact}(x-1) & x-2 \geq 0 \\ 1 & \text{otherwise} \end{cases}$$
ちょっとやり過ぎ感がありますが、わかりやすさ重視でこちらを採用しようと思います(もちろん$H_1(x)$を使った方法でも数式的には問題ありません)。
無限の長さのテープ
さて、再帰と分岐が出来るようになった(した)ところで、いざチューリングマシンを実装しようとすると、もう一つ問題があることに気づきます。
そう、無限の長さのテープをどう扱うか、です。
これも色々方法はありそうですが(無限次元ベクトルを許す、無限個のエッジの存在を許す、再帰で頑張る(?)など)、実は $\text{Floor}(x)$ と $2^x$ を活性化関数として追加するだけで出来てしまいます。ちょっと力技ですが。
テープの表現
私の趣味を通しつつ議論を簡単にするため、テープに以下の条件を課します:
- テープは左右両方に無限に長い
- 文字は
0と1のみ。空白文字は許しません - テープの初期状態(つまり入力)には、
1は有限個しかない
このとき、テープの状態は1つの(非負)実数だけで表すことが出来ます。
$i$ 番目 ($i \in \mathbb{Z}$)の文字を $t_i$ として
$$ t = \sum_{i \in \mathbb{Z}} 2^i t_i $$
この和は先程の条件から、実質有限和となり収束することが保証されます。チューリングマシンによって有限回の操作が行われた後でも、1は有限個しか存在しません。
これでテープの状態を表現することが出来ましたが、これだけでは不十分です。
テープへの操作
テープ $t$ に対して、「$i$ 番目を読む」「$i$ 番目に文字 $c$ を書き込む」という操作が出来る必要があります。
まず読み込みです。いきなり答えから書くと、
$$\text{Read}(t, i) = \text{Floor}(2^{-i}\cdot (t-2^{i+1}\cdot \text{Floor}(2^{-i-1}\cdot t)))$$
一見ぎょっとすると思いますが、やってることは
- $t$ を右に $i+1$ シフト => $2^{-i-1}\cdot t$
- floorして小数点以下を消す => $\text{Floor}(2^{-i-1}\cdot t)$
- 左に $i+1$ シフトして戻す => $2^{i+1}\cdot \text{Floor}(2^{-i-1}\cdot t)$
- 出来たものを $t$ から引くことで、$i$ より上の桁を消去 => $t - 2^{i+1}\cdot \text{Floor}(2^{-i-1}\cdot t)$
- 右に $i$ シフトして floor
という感じです。
この式は $\text{Floor}(x)$, $2^x$, および掛け算のみで構成されているため、活性化関数として $\text{Floor}(x)$, $2^x$, $x^2$ を採用すればネットワークとしてこれを表現出来ることがわかります(図はめんどいので省略)。
読み込みが出来れば書き込みは簡単で、
$$ \text{Write}(t, i, c) = t - 2^i \cdot \text{Read}(t, i) + 2^i \cdot c$$
$t$ から $i$ 桁目を消して $c$ を $i$ 桁目に挿入します。
チューリングマシンを作る
さあいよいよラスボスとの戦いです。
まずパーティとなる、登場人物を確認しましょう:
- $s \in \mathbb{N} \cup \{0, -1\}$ : マシンの状態。初期状態は
0で、受理状態は便宜上-1とします - $t \in \mathbb{R}_{\geq 0}$ : テープの状態
- $p \in \mathbb{Z}$ : ヘッドの位置。最初は 0 とします
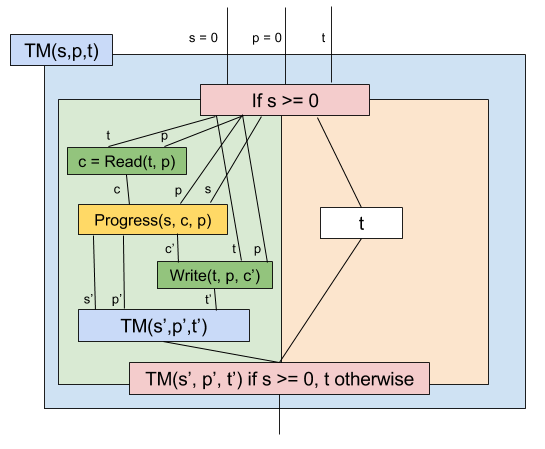
全体像は以下のようにすれば良いでしょう:
(この図は他と違い、エッジの脇には線形結合の係数ではなく伝播される値を書いています)
$s', p', t', c'$ は次の(遷移後の)状態やヘッドの位置などを表しています。
この関数は $s, p, t$ を受取り、プログラムを実行した後の最終的なテープの状態を出力としています。
受理状態、つまり $s = -1 \lt 0$ であればテープ $t$ をそのまま返します。
受理状態でなければ状態遷移を行います。$\text{Read}$ して $\text{Progress}$ して $\text{Write}$ して最後に再帰すればいいですね。
いやいや、Progressって何だよ。
Progress関数
ここが最後の肝、ラスボスの弱点です。
チューリングマシンのプログラムは、
$$\{(s_i, c_i, c_i', d_i, s_i') \mid 0 \leq i \lt N \} $$
というコマンド列で表現されます。
これは、**「状態が $s_i$ の時に文字 $c_i$ を読んだら、そこを $c_i'$ にし、 $d_i \in \{1, -1\}$ だけヘッドを移動させ、状態を $s_i'$ にする」**という意味です。
Progress関数はこれに対応するもので、 状態 $s$、読んだ文字 $c$、(便宜上)ヘッドの位置 $p$ を与えると、上記コマンドのうち対応するものが走り、新たな状態 $s'$、そこに挿入されるべき新たな文字 $c'$、次のヘッドの位置 $p'$ を計算します。
「$s$ が $s_i$ の時」とかをケアしたいので、半開区間の特性関数を、$H_1$ を使って作ります。$a \lt b$ に対して、
$$ I_{[a, b)}(x) = H_1(x-a) - H_1(x-b) = \begin{cases} 1 & x \in [a, b) \\ 0 & \text{otherwise} \end{cases}$$
これにより、Progress関数の各成分は次のように表せます:
$$\begin{eqnarray}
\text{Progress}_{s'}(s, c, p) &=& \sum_{i = 0}^N s_i \cdot I_{[s_i-0.5, s_i+0.5)}(s) \cdot I_{[c_i-0.5, c_i+0.5)}(c) \\
\text{Progress}_{c'}(s, c, p) &=& \sum_{i = 0}^N c_i \cdot I_{[s_i-0.5, s_i+0.5)}(s) \cdot I_{[c_i-0.5, c_i+0.5)}(c) \\
\text{Progress}_{p'}(s, c, p) &=& p + \sum_{i = 0}^N d_i \cdot I_{[s_i-0.5, s_i+0.5)}(s) \cdot I_{[c_i-0.5, c_i+0.5)}(c)
\end{eqnarray}$$
ここで注意したいのは、これをネットワークとして表現した時に、各成分で $N$個 (の固定数倍)のノードが必要になるということです。つまり、コマンドの数が増えるほど、必要なノードの個数が線形に増えてしまいます。
もしかしたらうまい方法があるかもしれませんが、ここはとりあえず妥協して、 1つのネットワークで表せるのはコマンドが$N$個以下のプログラムだけということを受け入れます。
完成
以上で完成です。お疲れ様でした。
ポイントをまとめておくと、
- 使った活性化関数は $H_1(x)$, $x^2$, $\text{Floor}(x)$, $2^x$ の4つ
- 再帰の機構を導入した
- 分岐の機構を導入したが、遅延評価が出来ればこれは無くてもいい
- 1つのプログラムに対して係数の組み合わせが1つ存在し、そのプログラムを表現している
- 1つのネットワークで表せるのはコマンドがN個以下のプログラムだけ(だが、ここはうまいことやる方法があるかもしれない)
注意
はじめにも断っていますが、このネットワークで機械学習は出来ません。頑張れば出来るかもしれませんが、微分可能性どころか連続性すら捨ててしまっているので相当大変です(うまくやれば$C^\infty$に出来るかもしれませんが)。
このネットワークは対象の関数を近似しているのではなく、exactにその関数に一致するパラメータの組を持つ、というところに意味があると思っています。
しかしこれではダメで、「目的の関数を知らなくても、パラメータ(線形結合の係数)をいじっていくうちに目的の関数に近づく」というNNの良さが失われてしまっています。
んー?