0 はじめに
初めまして、a1048576です。
2024年4月13日のABC349にて、橙パフォをだして入黄することができました。
入黄するまでにやったことなど書いていきます。
1 自己紹介
そもそも記事を書くのが初めてなので、軽く自己紹介していきます。
現高1で、中1になってすぐに競プロを始めました。ただ、中2の3月ごろまでは殆ど競プロをやっていなかったので、実質的には競プロ歴は1年ちょいです。
数学は割と得意な方だと思ってます。
レート推移はこんな感じです。
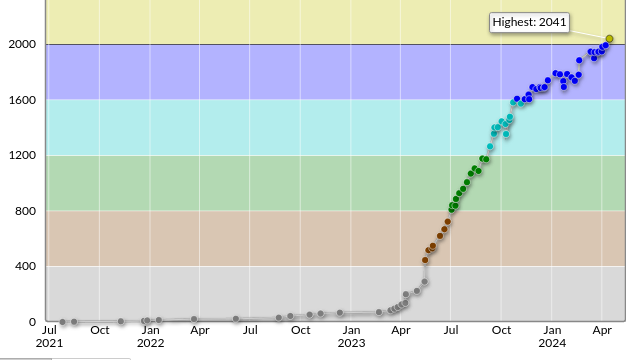
2-1 競プロを始めたきっかけ
中学に入学してすぐにパソコン部に興味を持ち、入部しました。そこで競プロやAtCoderの存在を知り、AtCoderアカウントを作成しました。
初めのうちはそれなりに競プロに熱中していたのですが、最初に参加したABC211でまさかの0完、パフォーマンス4を叩き出してしまいました。あまり覚えていませんが、競プロをほぼやらなくなったきっかけは多分これです。

その時の順位表。当時の僕はdouble型の存在を忘れていたようです。
その後、たまにAtCoderの存在を思い出してはコンテストに数分間だけ参加するなど、競プロへの興味は限りなく0に近いところまで落ちていました。
2023年2月までは。
2-2 競プロを再びやり始めたきっかけ
2023年2月、パ研合宿への参加を決めました。何で参加しようとしたかは覚えてないです。
そこで、当時レートが67しかなかった僕は、「流石にこのレートでパ研合宿に参加するのはまずい」と考え、再び競プロをやり始めました。その結果、この時からコンテストに毎週参加するようになり、パ研合宿開始までにレートは107まで伸びました。
(あれ、大して変わってなくね...?)
しかし、合宿参加者のレベルには到底ついていけず、合宿内のコンテストでは全てオンサイト最下位でした。ただ、合宿に参加したことで分かったことが1つありました。
「競プロ楽しい!!!」
それから、平均して1日1時間以上は競プロをするようになり、レートの伸びも大幅に速くなりました。
そして、2023年5月14日、ARC160にてB問題を通し、初の水パフォで入茶しました。

3 それからの成長
3-1 入緑、入水するまで
茶色になると、ただ愚直に計算するだけでなく、計算量の改善が必要になってきます。そこで、競プロで必要なアルゴリズムを学ぶようになりました。
具体的には、この記事に書かれていたアルゴリズムをそのまま全て覚えました。
https://qiita.com/e869120/items/eb50fdaece12be418faa
その勢いで、2023年7月1日のABC308で初の6完を達成し入緑、同年9月9日のABC319で青パフォを出して入水しました。

3-2 入青するまで
このころから、早解きにより青パフォや黃パフォを連続で出せるようになり、10月28日のABC326で青パフォをだして青コーダーになりました。特に新しいアルゴリズムを使ったりはせず、覚えたアルゴリズムを使ってひたすら過去問を埋め続けていました。

3-3 入黄するまで
青コーダーまではほぼノンストップでなれましたが、ここからが本当にきつかったです。
緑や水下位までを早解きするだけでもそれなりに多くの回で青パフォは出すことができましたが、それでは黄色にはなれません。そのため、青diffの問題を安定して解く必要があります。
しかし、これが本当に難しい。青まですぐに行けたんだから黄色なんて余裕やろとか思ってた当時の僕をぶん殴りたいです。
高難易度の問題を見て、長時間考察しても分からなかったら解説を見て、知らないアルゴリズムを見つけてすぐに実装する、などというように精進をひたすら続けていました。それにより、少しづつレートが伸びてきて、ABCでカンストパフォを出したり、ARCやAGCでも暖色パフォを出したりするようになりました。
そして、2024年4月13日のABC349でカンストパフォを出し、ついに入黄することができました。

4 精進について
結局、「問題を解けば成長する」というのが本質なのには変わりないですが、ここでは自分がやってきた精進方法をまとめていきます。基本的には最初から今までやっていることは同じです。
4-1 低難易度埋めは効果があるか
低難易度を埋めることは意味がない、というのは考察力だけを見たときの話であり、コンテストで勝つことを考えたら低難易度埋めはとても効果があると思います。
実際、これにより問題文を素早く読み取る能力や、タイピング力は大きく上がったと思っており、僕が早解きが得意になった、最も大きな理由だと考えています。
4-2 解説をいつ見るか
僕の場合、その問題が水diff以下なら2時間、青diff以上なら5時間は考察をするようにしています。ARCやAGCの問題の場合これの2倍の時間は粘ります。
低難易度の問題の場合、典型的なアルゴリズムや考察によって解ける場合が殆どなので、ある程度考察したら解説を見て実装するようにしています。一方、高難易度の問題はそうはいかない場合が多いので、考察をして分からなくても解説を見ずに放置することも多いです。
4-3 Streakを繋ぐべきか
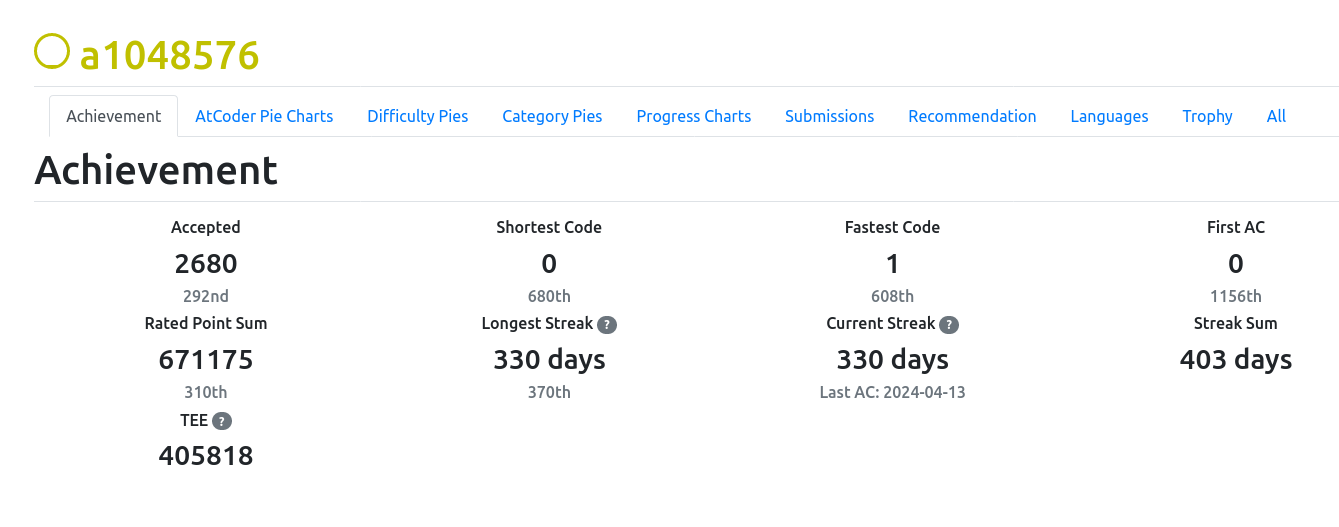
Streakを繋ぐことだけを考えてしまうと、灰diffを1問だけ解いて精進した気になってしまうので良くないです。実際、僕は現在Streakを330日繋いでいますが、中には灰diffを1問解いているだけの日もあります。
しかし、モチベーションを維持することを考えるなら、Streakを繋ぐのは効果的だと思います。
実際、僕は中1のときに少し成績が悪かっただけですぐに競プロをやめてしまったような人なので、競プロのモチベーションを落とさないためにStreakを繋ぐことはかなり効果がありました。
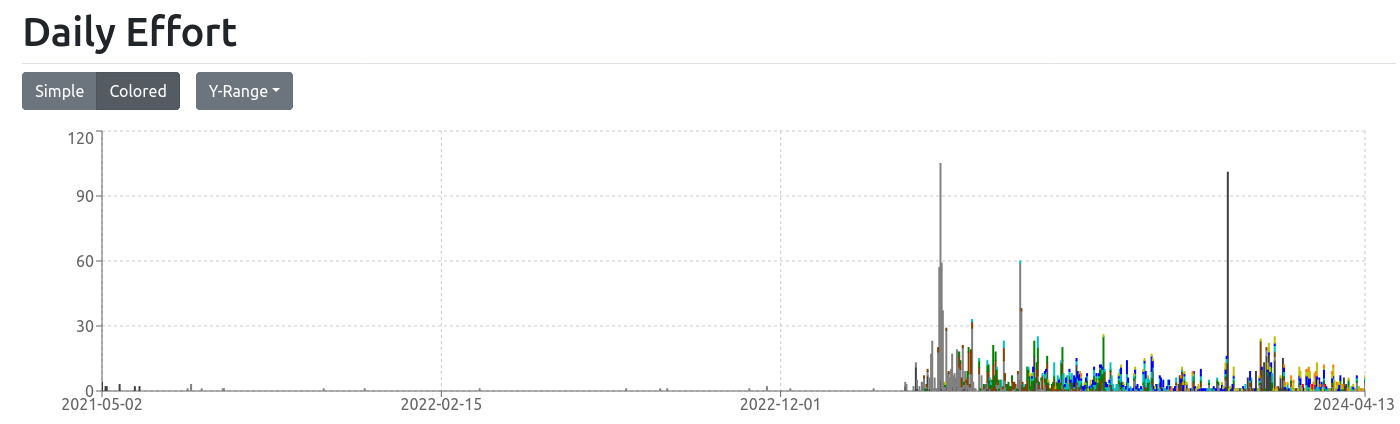
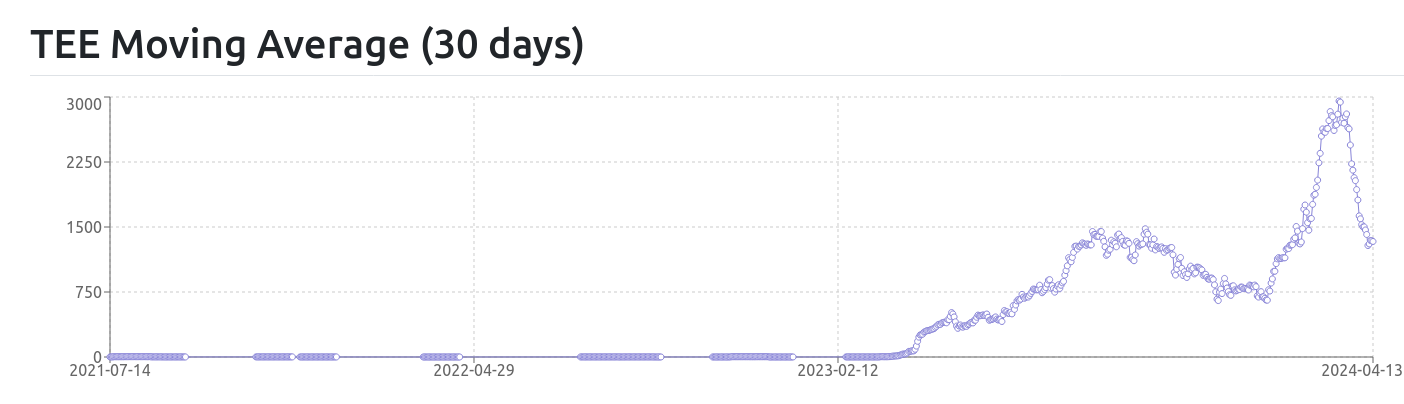
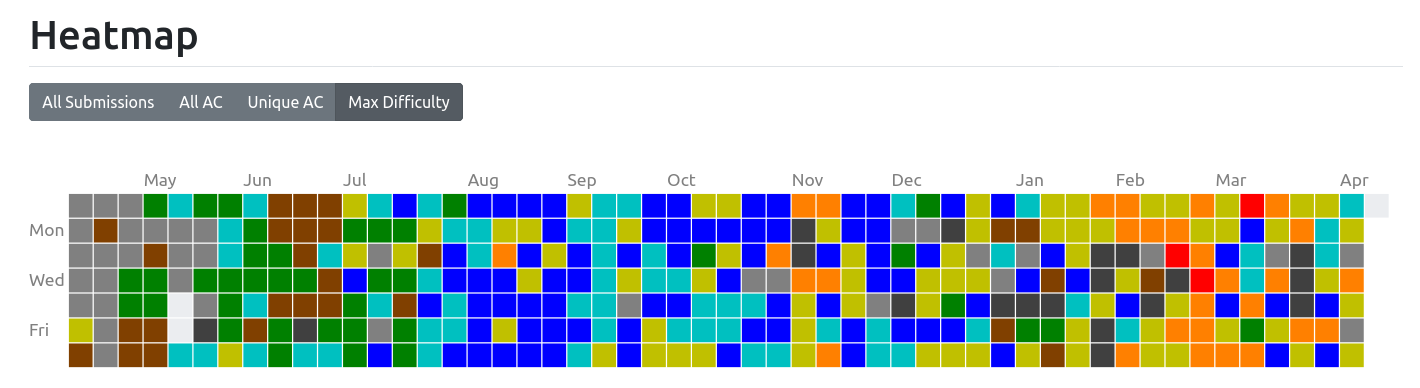
4-4 精進記録
5 覚えたアルゴリズム
黄色になるまでに覚えたアルゴリズムやデータ構造を、理解度で5段階に分けます。
| 名称 | 理解度 |
|---|---|
| 素数判定 | 5 |
| 素因数分解 | 5 |
| 二分探索 | 5 |
| 全探索 | 5 |
| 順列全探索 | 5 |
| bit全探索 | 5 |
| 累積和 | 5 |
| 半分全列挙 | 5 |
| 三分探索 | 3 |
| 尺取り法 | 5 |
| 繰り返し二乗法 | 5 |
| 逆元 | 5 |
| ユークリッドの互除法 | 2 |
| 座標圧縮 | 5 |
| ローリングハッシュ | 4 |
| ナップサックDP | 5 |
| 区間DP | 4 |
| 期待値DP | 4 |
| bitDP | 5 |
| 確率DP | 5 |
| 桁DP | 4 |
| 木DP | 5 |
| 全方位木DP | 4 |
| 二乗の木DP | 3 |
| 耳DP | 3 |
| 挿入DP | 2 |
| 行列累乗 | 5 |
| ダブリング | 5 |
| Grundy数 | 5 |
| 平方分割 | 4 |
| 平面走査 | 2 |
| ダブリング | 5 |
| LCS | 4 |
| LIS | 4 |
| FFT | 3 |
| Mo's Algorithm | 4 |
| セグ木 | 5 |
| 遅延セグ木 | 3 |
| Wavelet Matrix | 1 |
| BFS | 5 |
| DFS | 5 |
| ダイクストラ法 | 5 |
| ベルマンフォード法 | 4 |
| ワーシャルフロイド法 | 5 |
| クラスカル法 | 4 |
| プリム法 | 2 |
| UnionFind | 5 |
| トポロジカルソート | 4 |
| 二部グラフ判定 | 3 |
| 強連結成分分解 | 2 |
| オイラーツアー | 4 |
6 終わりに
茶色から青色になるまでの期間よりも、青色から黄色になるまでの期間の方が長かったです。橙色までは更に遠い道のりになりそうですが、まずはARCでレートをキープすることを目標に頑張りたいです!