本記事は U-TOKYO AP Advent Calendar 2017 の15日目です。
はじめに
こんにちは。東京大学工学部 計数工学科 の @_yuki です。
師走も半ばとなり、何かと慌ただしくなってきました。忘年会や帰省なんかもあり、鉄道で移動される方も多いのではないでしょうか。本記事では、そんな風に**真っすぐ目的地に向かうだけが鉄道じゃない!**とばかりに、駅名でしりとりをしてみたいと思います。
ちなみに、単に最長しりとりを構成するだけなら、既に研究対象としても繰り返し取り上げられ[^1]、優れた解法が存在します。卒論で扱ってねとらぼの記事[^2]になった方もいるようで、別の方が実装[^3]されたものもあるので、しりとりの解のみ欲しい方はそちらへどうぞ。
この記事では、**あえて整数計画法のソルバーは使わずに、東京メトロの全143駅から最長しりとりを構成していきます。それによって、このような問題はどのように定式化すると楽なのか?**を考える一例となれればと思います。厳密でないところが一部あります[^4]が、気にしない。
ルール
- 東京メトロの駅だけを使い、駅名でしりとりをしながら回る。
- 同じ駅を使うことなく、なるべくたくさんの駅を回るのが目標。
- 移動経路は不問(どこを目指すかだけでしりとり)。
- 濁点と半濁点は無視、拗音は小文字を大文字に取り換える。つまり「和光市」→「神保町」や「北千住」→「有楽町」を認める。
- 副駅名は連結してもしなくてもよい。つまり「明治神宮前」「明治神宮前<原宿>」はいずれか片方を採用。
考え方
駅名は「矢印」
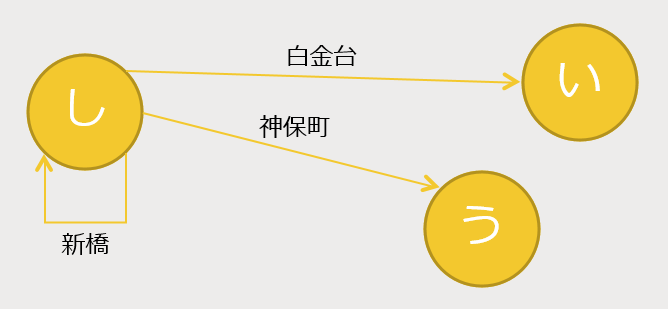 しりとりで大事なのは最初と最後の文字だけなので、駅名を**ひらがなからひらがなへの矢印**として考えます。
例えば「白金台」は「し」で始まり「い」で終わるので、「し」から「い」への矢印です。「新橋」は「し」から「し」に戻ってくる矢印です。
## ループと直線に分ける
### ループと直線の考え方
しりとりで大事なのは最初と最後の文字だけなので、駅名を**ひらがなからひらがなへの矢印**として考えます。
例えば「白金台」は「し」で始まり「い」で終わるので、「し」から「い」への矢印です。「新橋」は「し」から「し」に戻ってくる矢印です。
## ループと直線に分ける
### ループと直線の考え方
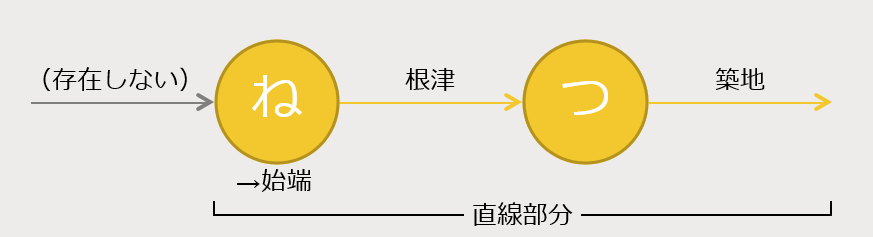
 しりとりをしていると、いくつかの単語のあと、同じひらがなに戻ってくることがあります。このような円の集まりを矢印の図で見ると、**ループ**が出来上がっています。ループ内ではしりとりの成立条件が単純になるので、しりとりをループとそれ以外の**直線部分**に分けて考えます。最終的には、直線を始端から進み、途中からループに入り、ループを抜けてから再び直線を終端へ向かう経路(上図)が、最長しりとりになります。
### ループ候補と直線候補の分別
しりとりをしていると、いくつかの単語のあと、同じひらがなに戻ってくることがあります。このような円の集まりを矢印の図で見ると、**ループ**が出来上がっています。ループ内ではしりとりの成立条件が単純になるので、しりとりをループとそれ以外の**直線部分**に分けて考えます。最終的には、直線を始端から進み、途中からループに入り、ループを抜けてから再び直線を終端へ向かう経路(上図)が、最長しりとりになります。
### ループ候補と直線候補の分別
 最長しりとりの始端に来るひらがなを考えてみましょう。もしこのひらがなで終わる駅があれば、しりとりはもっと長くできます。よって、始端のひらがなには、それで始まる駅だけしかないと分かります。
逆に考えると、あるひらがなに対して、**そのひらがなで始まる駅しか存在しないならば、そのような単語は始端にしか使えません**。この操作を繰り返すと、始端につながる直線部分に使いうる駅を取り出すことができます。終端についても同様です。
そして、**残った駅は、前後をたどっていっても行き止まりにならないものだけ**になっています。これはつまり、ループを作るときに使う駅の候補ということです。
上図の例で説明します。メトロに「ね」で終わる駅はありません。よって「根津」は始端にしか使えないと分かります。さらに、「つ」で終わる駅は根津しかありません。よって「築地」は根津から続く直線にしか使えないのです。これを繰り返すことで、直線候補が取り出せます。一方、取り出されずに最後まで残った駅がループ候補です。
## ループの最長化
### ひらがなへの出入りのバランス
最長しりとりの始端に来るひらがなを考えてみましょう。もしこのひらがなで終わる駅があれば、しりとりはもっと長くできます。よって、始端のひらがなには、それで始まる駅だけしかないと分かります。
逆に考えると、あるひらがなに対して、**そのひらがなで始まる駅しか存在しないならば、そのような単語は始端にしか使えません**。この操作を繰り返すと、始端につながる直線部分に使いうる駅を取り出すことができます。終端についても同様です。
そして、**残った駅は、前後をたどっていっても行き止まりにならないものだけ**になっています。これはつまり、ループを作るときに使う駅の候補ということです。
上図の例で説明します。メトロに「ね」で終わる駅はありません。よって「根津」は始端にしか使えないと分かります。さらに、「つ」で終わる駅は根津しかありません。よって「築地」は根津から続く直線にしか使えないのです。これを繰り返すことで、直線候補が取り出せます。一方、取り出されずに最後まで残った駅がループ候補です。
## ループの最長化
### ひらがなへの出入りのバランス
 まずは、ループをなるべく長くすることを考えます。
ループは最終的に一周するので、それぞれのひらがなへ**入る矢印と出る矢印の数は同じ**になるはずです。バランスが取れていないなら、しりとりを形成するにはその分、矢印(駅)を減らさなければなりません。
上図の例では、「せ」に入る矢印は「北綾瀬」1本なのに、出る矢印は「千川」「千駄木」の2本なので、どちらかを切らなければループの部品にならないと分かります。
### お互いにとって余る矢印から切る
まずは、ループをなるべく長くすることを考えます。
ループは最終的に一周するので、それぞれのひらがなへ**入る矢印と出る矢印の数は同じ**になるはずです。バランスが取れていないなら、しりとりを形成するにはその分、矢印(駅)を減らさなければなりません。
上図の例では、「せ」に入る矢印は「北綾瀬」1本なのに、出る矢印は「千川」「千駄木」の2本なので、どちらかを切らなければループの部品にならないと分かります。
### お互いにとって余る矢印から切る
 矢印には、出所と行先があります。あるひらがなの出入りをつり合わせようとして矢印を切ったら、その矢印がつながっている**もう片方のひらがなのバランスを崩してしまうかも**しれません。
そこで、出て行く矢印が余っているひらがな(以下、赤色で示します)と、入って来る矢印が余っているひらがな(以下、青色で示します)の間の駅を優先的に切ります。こうすることで、**2つのひらがな両方にとって不要な矢印から消していく**ことができます。
上図の例では、「み」は出る矢印が余っている、「ゆ」は入る矢印が余っているので、その間を結ぶ「南千住」を切ってあげると、どちらのひらがなもバランスのとれた状態に近づきます。
### 切り足りない分は他を破壊
矢印には、出所と行先があります。あるひらがなの出入りをつり合わせようとして矢印を切ったら、その矢印がつながっている**もう片方のひらがなのバランスを崩してしまうかも**しれません。
そこで、出て行く矢印が余っているひらがな(以下、赤色で示します)と、入って来る矢印が余っているひらがな(以下、青色で示します)の間の駅を優先的に切ります。こうすることで、**2つのひらがな両方にとって不要な矢印から消していく**ことができます。
上図の例では、「み」は出る矢印が余っている、「ゆ」は入る矢印が余っているので、その間を結ぶ「南千住」を切ってあげると、どちらのひらがなもバランスのとれた状態に近づきます。
### 切り足りない分は他を破壊
 とはいえ、いつもそううまく行くとは限りません。お互いに余る矢印だけでは切り足りず、**つり合っているひらがなとの矢印を切るしかない**場合があります。
また、切れる選択肢がありすぎる場合も問題です。全ての相手を切ることができないため、**切断対象に選ばれなかった相手は別のひらがなとの矢印を切る**ことになってしまうからです。
上図の例で、出る矢印が余っている「み」に注目してみましょう。入る矢印が余る「え」「く」「わ」全てへの矢印を切ったとしても、まだつり合いがとれていません。仕方がないので、仮に「南砂町」を切ったとします。すると「ち」のバランスを崩してしまい、「ち」から出る矢印も1本新たに切る必要が出てしまいます。
### 切る選択肢が多いどうしなら切らなくてよい
とはいえ、いつもそううまく行くとは限りません。お互いに余る矢印だけでは切り足りず、**つり合っているひらがなとの矢印を切るしかない**場合があります。
また、切れる選択肢がありすぎる場合も問題です。全ての相手を切ることができないため、**切断対象に選ばれなかった相手は別のひらがなとの矢印を切る**ことになってしまうからです。
上図の例で、出る矢印が余っている「み」に注目してみましょう。入る矢印が余る「え」「く」「わ」全てへの矢印を切ったとしても、まだつり合いがとれていません。仕方がないので、仮に「南砂町」を切ったとします。すると「ち」のバランスを崩してしまい、「ち」から出る矢印も1本新たに切る必要が出てしまいます。
### 切る選択肢が多いどうしなら切らなくてよい
 逆に、お互いにとって余る矢印なのに、切らないほうが良い例も存在します。それは、**切れる選択肢がありすぎるひらがな同士**を結ぶ矢印の場合です。その矢印を切らなかったとしても、双方のひらがなともつり合いを達成できるので、実は消す意味がありません。
上図の例で、「し」は出る矢印が2本、「わ」は入る矢印が2本余っているだけです。しかし切断の選択肢、つまり相手側で余っている矢印はそれぞれ7本と4本あります。だったらわざわざ「白金高輪」を切らずとも、他の切ってほしそうにしているひらがなとの矢印を切れば事足ります。
## 直線の最長化
### 長い始まりと終わりを選ぶ
当たり前ですが、直線部分の候補のうち長いものを使うのが良いです。ループ中のどのひらがなで直線と接続するかは自由なので、**始端側と終端側につながる直線の長さの和が最大**となるひらがなを選びます。
### ループから排除されても1経路復活する
逆に、お互いにとって余る矢印なのに、切らないほうが良い例も存在します。それは、**切れる選択肢がありすぎるひらがな同士**を結ぶ矢印の場合です。その矢印を切らなかったとしても、双方のひらがなともつり合いを達成できるので、実は消す意味がありません。
上図の例で、「し」は出る矢印が2本、「わ」は入る矢印が2本余っているだけです。しかし切断の選択肢、つまり相手側で余っている矢印はそれぞれ7本と4本あります。だったらわざわざ「白金高輪」を切らずとも、他の切ってほしそうにしているひらがなとの矢印を切れば事足ります。
## 直線の最長化
### 長い始まりと終わりを選ぶ
当たり前ですが、直線部分の候補のうち長いものを使うのが良いです。ループ中のどのひらがなで直線と接続するかは自由なので、**始端側と終端側につながる直線の長さの和が最大**となるひらがなを選びます。
### ループから排除されても1経路復活する
 実は、直線を作るのはもともと直線候補だった矢印だけではありません。ループ候補に入っていたけれど、切られてしまい使われなかった矢印は、**直線候補として再利用**できるのです。
切断の経路は出る矢印が余るひらがなから入る矢印が余るひらがなまでつながっています。これら切断の起終点にあたるひらがなでループに出入りするようにしてやれば、ループの前または後ろへの連結によって、切られていた部分を復活できます。ただしもちろん、復活できるのは1経路だけです。
### 短い切断を増やして復活を長くする
実は、直線を作るのはもともと直線候補だった矢印だけではありません。ループ候補に入っていたけれど、切られてしまい使われなかった矢印は、**直線候補として再利用**できるのです。
切断の経路は出る矢印が余るひらがなから入る矢印が余るひらがなまでつながっています。これら切断の起終点にあたるひらがなでループに出入りするようにしてやれば、ループの前または後ろへの連結によって、切られていた部分を復活できます。ただしもちろん、復活できるのは1経路だけです。
### 短い切断を増やして復活を長くする
 では、復活する1経路を長くするためにはどうしたらよいでしょうか。もし、切断が中途半端に長いものばかりだったとしたら、どれが蘇ってもあまりうれしくありません。それよりも、**1つだけとても長い切断がある**方が、復活の効果は大きくなります。
ここで、ループ内にある出る矢印が余るひらがなや入る矢印が余るひらがなで余っている矢印の**総数**は一定です。つまり、切断の経路数も一定ですから、1つを長くするには**他の全てをなるべく短くする**べきです。
### 初めの解によって探索範囲が定まる
始まりと終わりの端が長くなるようなひらがなの選び方と、復活が長くなるようなひらがなの選び方は、一致するとは限りません。条件が異なれば、組み合わせるためには妥協が必要となり、各自は最長ではなくなってしまいます。
しかし最適化によって、**それぞれが到達できる上限の長さ**が分かります。よって、ばらばらに最長を目指したときに求まるしりとりを初めの解として、例えばそこから端の長さを上限に向けて増やしたときの増加分が、ループや復活に与える損を上回るようなものだけを探索すればよいと分かります。
# 実装
```vb.net:ChainWord
Option Explicit
Sub ChainWord()
Dim floop As Object, rloop As Object, fstraight As Object, rstraight As Object
BuildDictionary floop, rloop '辞書作成
DivideStraight floop, rloop, fstraight, rstraight '直線候補の分別
CutSurplus floop, rloop, fstraight, rstraight '余る矢印の切断
End Sub
```
では、復活する1経路を長くするためにはどうしたらよいでしょうか。もし、切断が中途半端に長いものばかりだったとしたら、どれが蘇ってもあまりうれしくありません。それよりも、**1つだけとても長い切断がある**方が、復活の効果は大きくなります。
ここで、ループ内にある出る矢印が余るひらがなや入る矢印が余るひらがなで余っている矢印の**総数**は一定です。つまり、切断の経路数も一定ですから、1つを長くするには**他の全てをなるべく短くする**べきです。
### 初めの解によって探索範囲が定まる
始まりと終わりの端が長くなるようなひらがなの選び方と、復活が長くなるようなひらがなの選び方は、一致するとは限りません。条件が異なれば、組み合わせるためには妥協が必要となり、各自は最長ではなくなってしまいます。
しかし最適化によって、**それぞれが到達できる上限の長さ**が分かります。よって、ばらばらに最長を目指したときに求まるしりとりを初めの解として、例えばそこから端の長さを上限に向けて増やしたときの増加分が、ループや復活に与える損を上回るようなものだけを探索すればよいと分かります。
# 実装
```vb.net:ChainWord
Option Explicit
Sub ChainWord()
Dim floop As Object, rloop As Object, fstraight As Object, rstraight As Object
BuildDictionary floop, rloop '辞書作成
DivideStraight floop, rloop, fstraight, rstraight '直線候補の分別
CutSurplus floop, rloop, fstraight, rstraight '余る矢印の切断
End Sub
```
BuildDictionary
Private Sub BuildDictionary(floop As Object, rloop As Object)
Dim word As Object, nrow As Long, tmpw As String, tmpc As String
'初期化
Set floop = CreateObject("Scripting.Dictionary")
Set rloop = CreateObject("Scripting.Dictionary")
nrow = 1
With Thisworkbook.Worksheets(1)
Do
'単語の取得
tmpw = .Cells(nrow, 1).Value
If tmpw = "" Then Exit Do
'始まりのひらがなによる辞書
tmpc = SplitSonant(Left$(tmpw, 1))
If Not floop.Exists(tmpc) Then
Set word = CreateObject("Scripting.Dictionary")
floop.Add tmpc, word
End If
floop(tmpc).Add tmpw, SplitSonant(Right$(tmpw, 1))
'終わりのひらがなによる辞書
tmpc = SplitSonant(Right$(tmpw, 1))
If Not rloop.Exists(tmpc) Then
Set word = CreateObject("Scripting.Dictionary")
rloop.Add tmpc, word
End If
rloop(tmpc).Add tmpw, SplitSonant(Left$(tmpw, 1))
nrow = nrow + 1
Loop
End With
End Sub
DivideStraight
Private Sub DivideStraight(floop As Object, rloop As Object, fstraight As Object, rstraight As Object)
Dim char As Variant, word As Variant, divide As Boolean, ntmps As Long, i As Long, tmps As Object, tmpw As Object, tmpc As String
'始端につながる直線候補
Set fstraight = CreateObject("Scripting.Dictionary")
Do
divide = False
For Each char In floop
If Not rloop.Exists(char) Then
For Each word In floop(char)
Set tmps = CreateObject("System.Collections.ArrayList")
'別の始端候補の後ろにつながるか
If fstraight.Exists(char) Then
ntmps = fstraight(char).Item(0).Count
For i = 0 To fstraight(char).Count - 1
tmps.Add fstraight(char).Item(i).Clone
Next
Else
ntmps = 1
End If
'直線候補に加える
Set tmpw = CreateObject("System.Collections.ArrayList")
For i = 1 To ntmps
tmpw.Add word
Next
tmps.Add tmpw
'ループとの接続点が同一の候補と統合
tmpc = floop(char)(word)
If fstraight.Exists(tmpc) Then
Select Case tmps.Count - fstraight(tmpc).Count
Case Is > 0
fstraight.Remove tmpc
fstraight.Add tmpc, tmps
Case 0
For i = 0 To tmps.Count - 1
fstraight(tmpc).Item(i).Addrange tmps.Item(i)
Next
End Select
Else
fstraight.Add tmpc, tmps
End If
'ループ候補から削除
rloop(tmpc).Remove word
If rloop(tmpc).Count = 0 Then rloop.Remove tmpc
Next
floop.Remove char
divide = True
End If
Next
Loop While divide
'終端につながる直線候補
Set rstraight = CreateObject("Scripting.Dictionary")
Do
divide = False
For Each char In rloop
If Not floop.Exists(char) Then
For Each word In rloop(char)
Set tmps = CreateObject("System.Collections.ArrayList")
'別の終端候補の前につながるか
If rstraight.Exists(char) Then
ntmps = rstraight(char).Item(0).Count
For i = 0 To rstraight(char).Count - 1
tmps.Add rstraight(char).Item(i).Clone
Next
Else
ntmps = 1
End If
'直線候補に加える
Set tmpw = CreateObject("System.Collections.ArrayList")
For i = 1 To ntmps
tmpw.Add word
Next
tmps.Insert 0, tmpw
'ループとの接続点が同一の候補と統合
tmpc = rloop(char)(word)
If rstraight.Exists(tmpc) Then
Select Case tmps.Count - rstraight(tmpc).Count
Case Is > 0
rstraight.Remove tmpc
rstraight.Add tmpc, tmps
Case 0
For i = 0 To tmps.Count - 1
rstraight(tmpc).Item(i).Addrange tmps.Item(i)
Next
End Select
Else
rstraight.Add tmpc, tmps
End If
'ループ候補から削除
floop(tmpc).Remove word
If floop(tmpc).Count = 0 Then floop.Remove tmpc
Next
rloop.Remove char
divide = True
End If
Next
Loop While divide
End Sub
CutSurplus
Cutsurplusについては改修中[^5]です。恐れ入りますが、公開まで今しばらくお待ちください。
SplitSonant
Private Function SplitSonant(str As String) As String '濁点や拗音などの処理
Dim nchar As Integer
'濁点と半濁点の削除
nchar = Asc(StrConv(Left$(StrConv(str, vbKatakana + vbNarrow), 1), vbHiragana + vbWide))
'拗音と促音の変換
Select Case nchar
Case -32097 To -32089, -32063, -32031 To -32027
If nchar Mod 2 = -1 Then
nchar = nchar + 1
End If
End Select
SplitSonant = Chr(nchar)
End Function