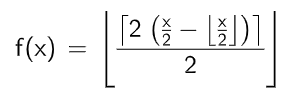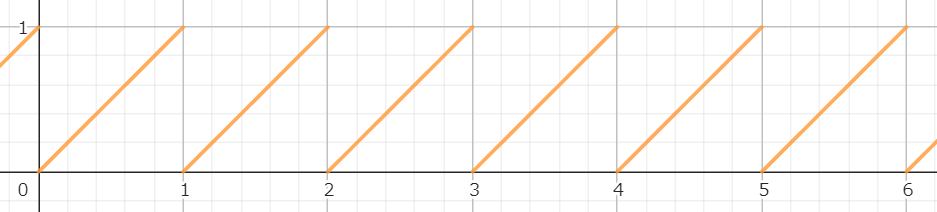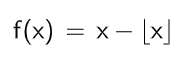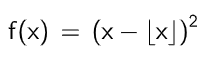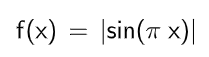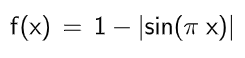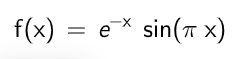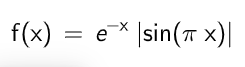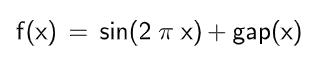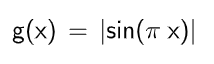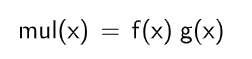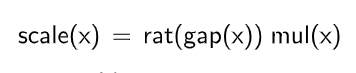概要
明滅などの反復的なマテリアルを作りたいとき、UE5ではいくつかの方法がある。
一番イメージ通りに作れるのは、適切なノードを打ったCurveデータを用意して、マテリアルのパラメータに流し込む方法だろう。
しかしこの方法ではCurveデータをプログラム（Blueprint）で制御しなければならない場合が多く、アーティスト単体では気軽に用いることができない。
そもそも反復的なグラフの殆どは数式で表せるはず。
ではマテリアルだけで様々な波形をつくろうではないか。
開発環境
UE5.0
基本グラフ
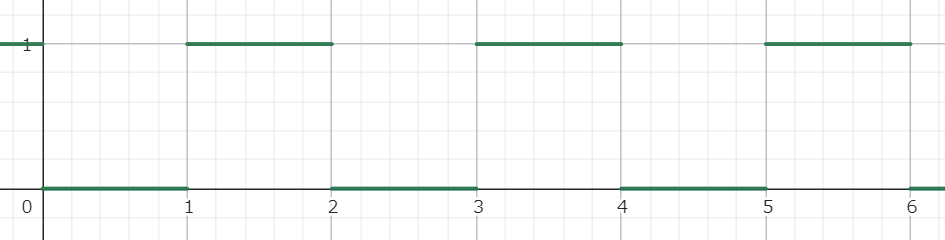
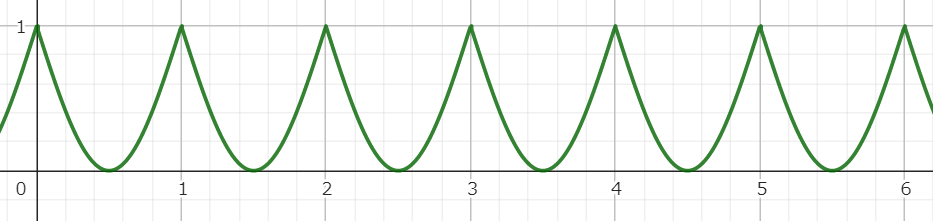
ここでは一周期（反復させたい範囲）を横軸x=1.0となるように数式を立てている。
※矩形波のみ例外。
矩形波
計算式
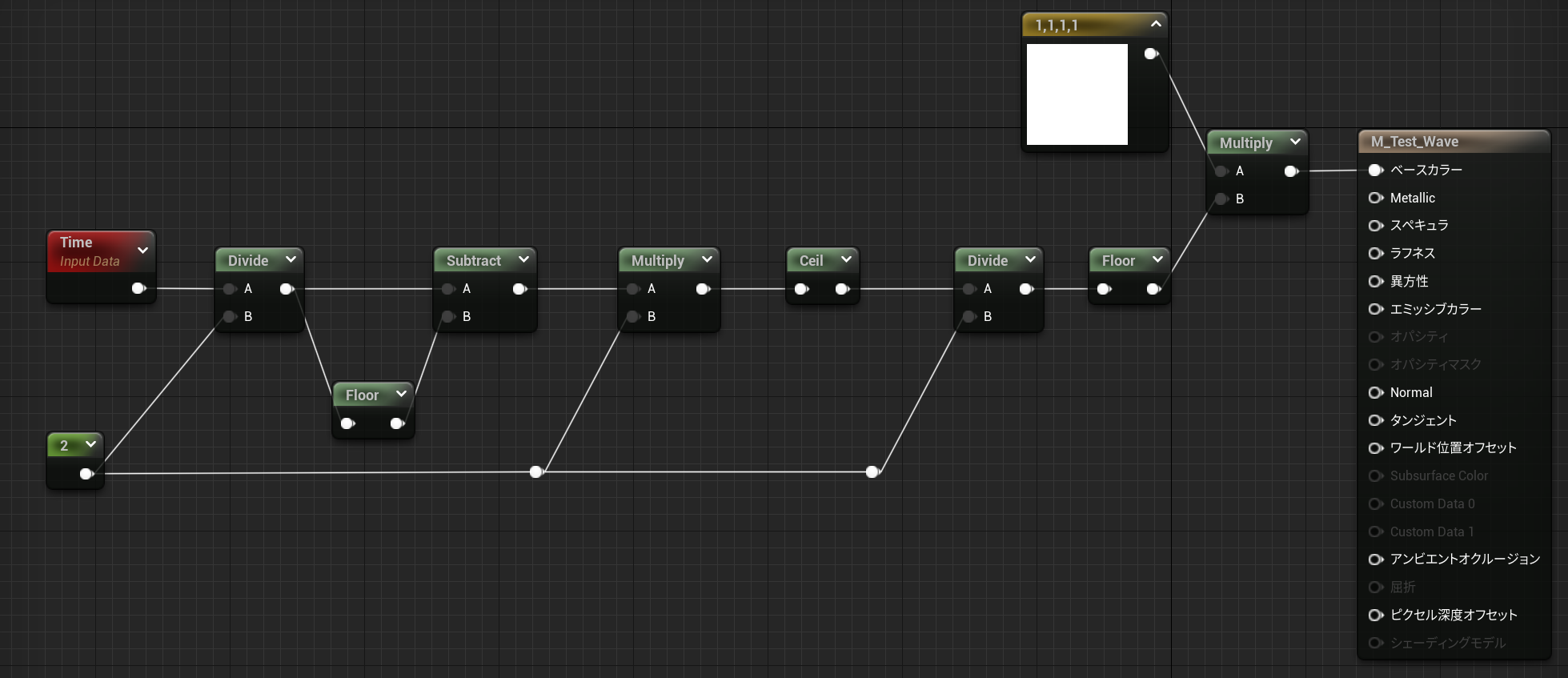
マテリアル
ノコギリ波
計算式
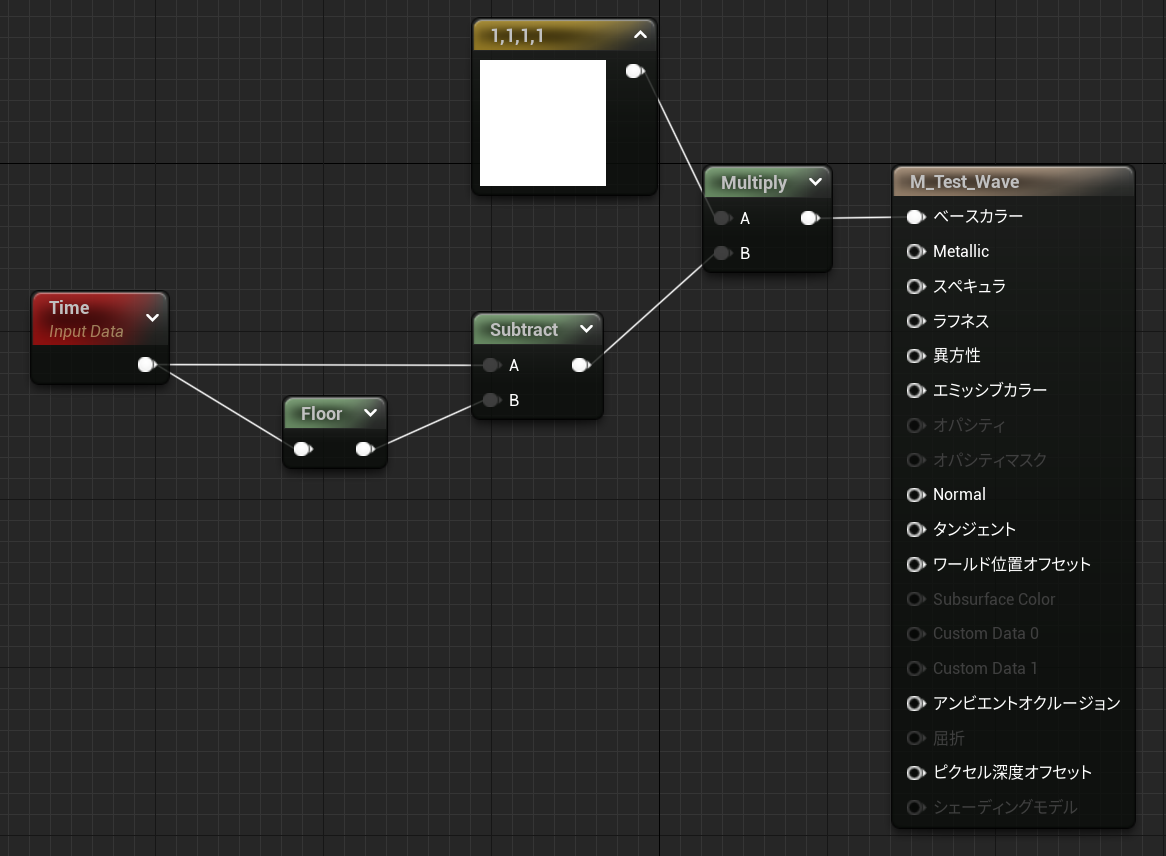
マテリアル
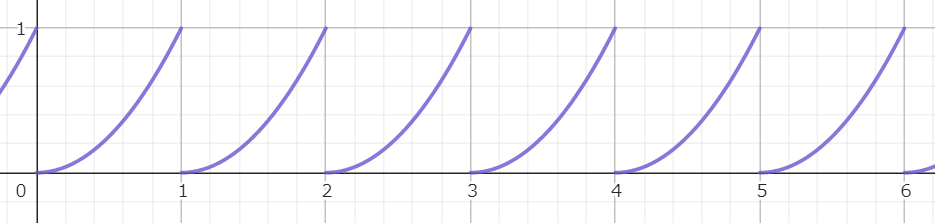
二次曲線ノコギリ波
計算式
マテリアル
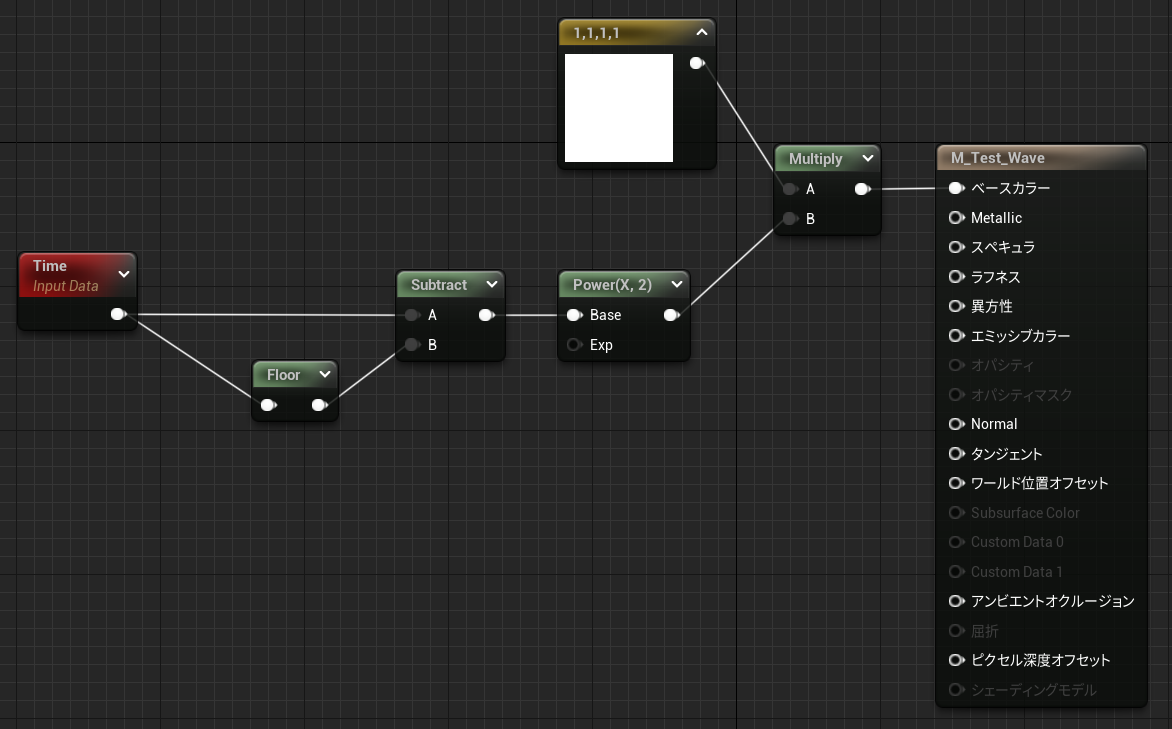
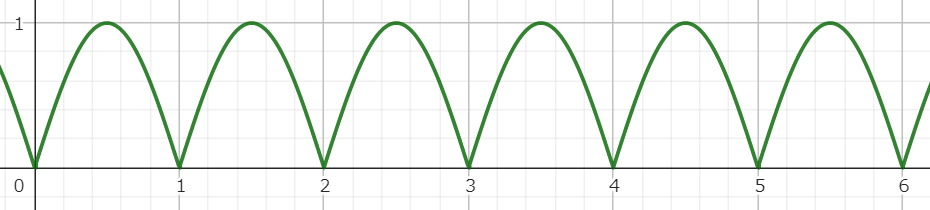
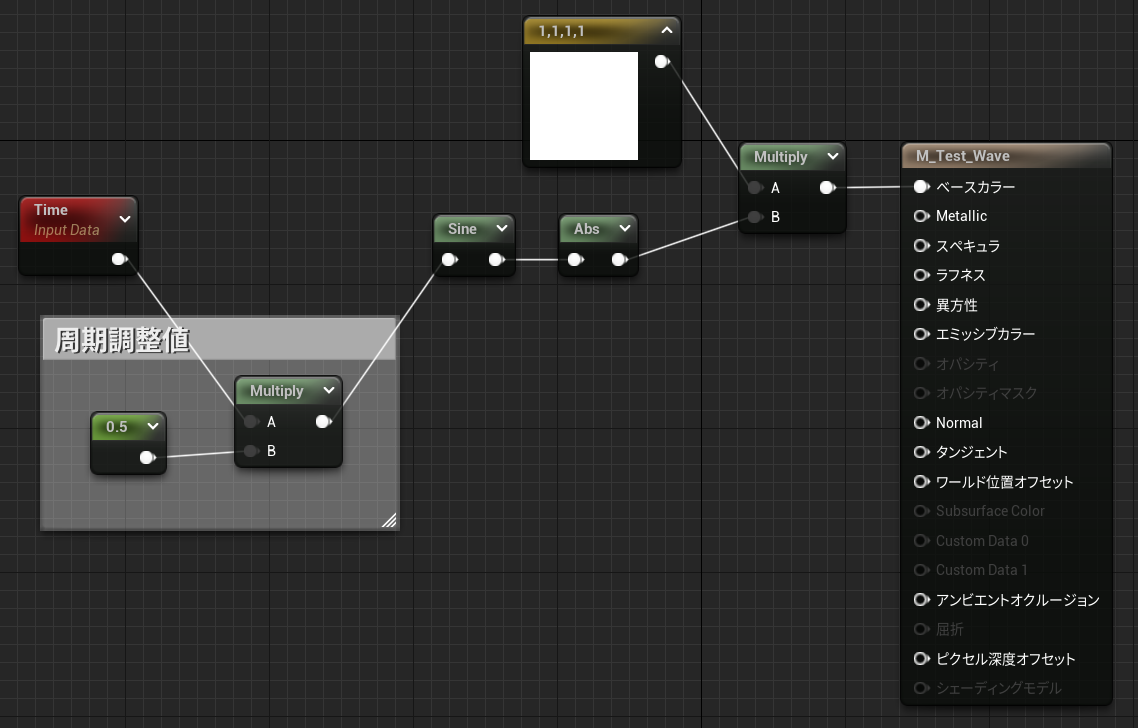
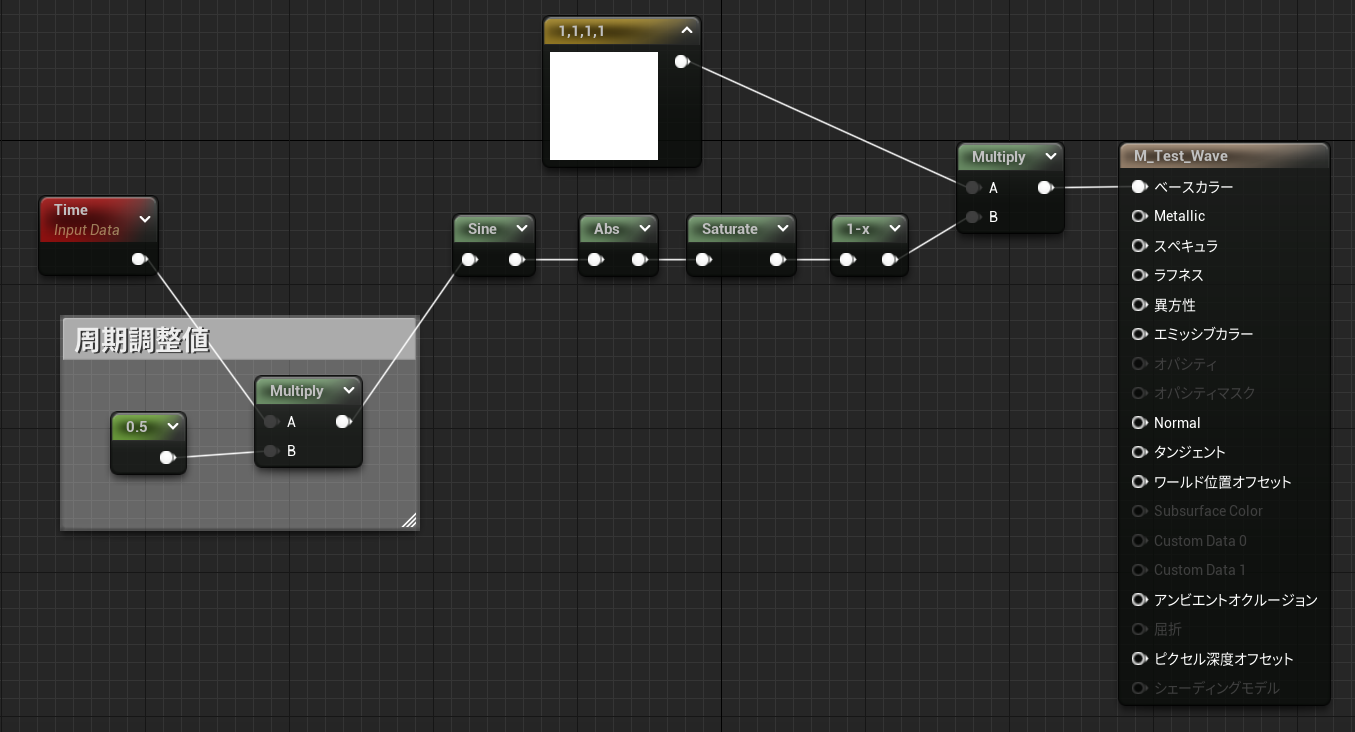
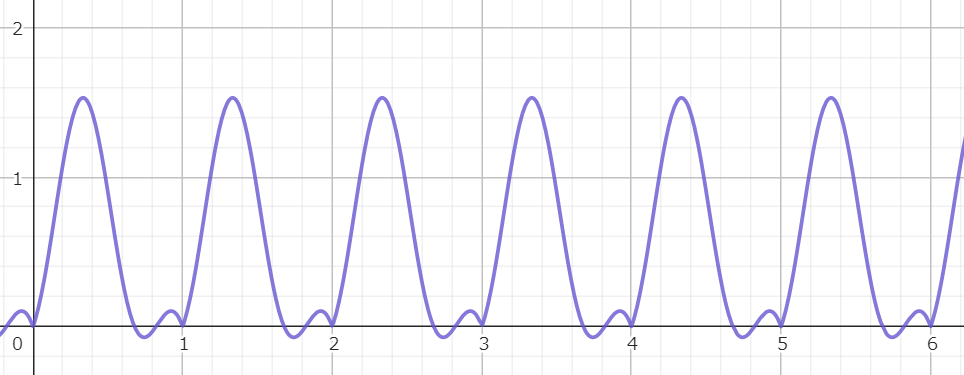
絶対値サイン波
計算式
マテリアル
絶対値サイン波（反転）
計算式
マテリアル
可変グラフ
反復させるとはいえ、ある程度の調整はかけられたほうがいい。
ここでは2種類の可変値を用いた波形を紹介する。
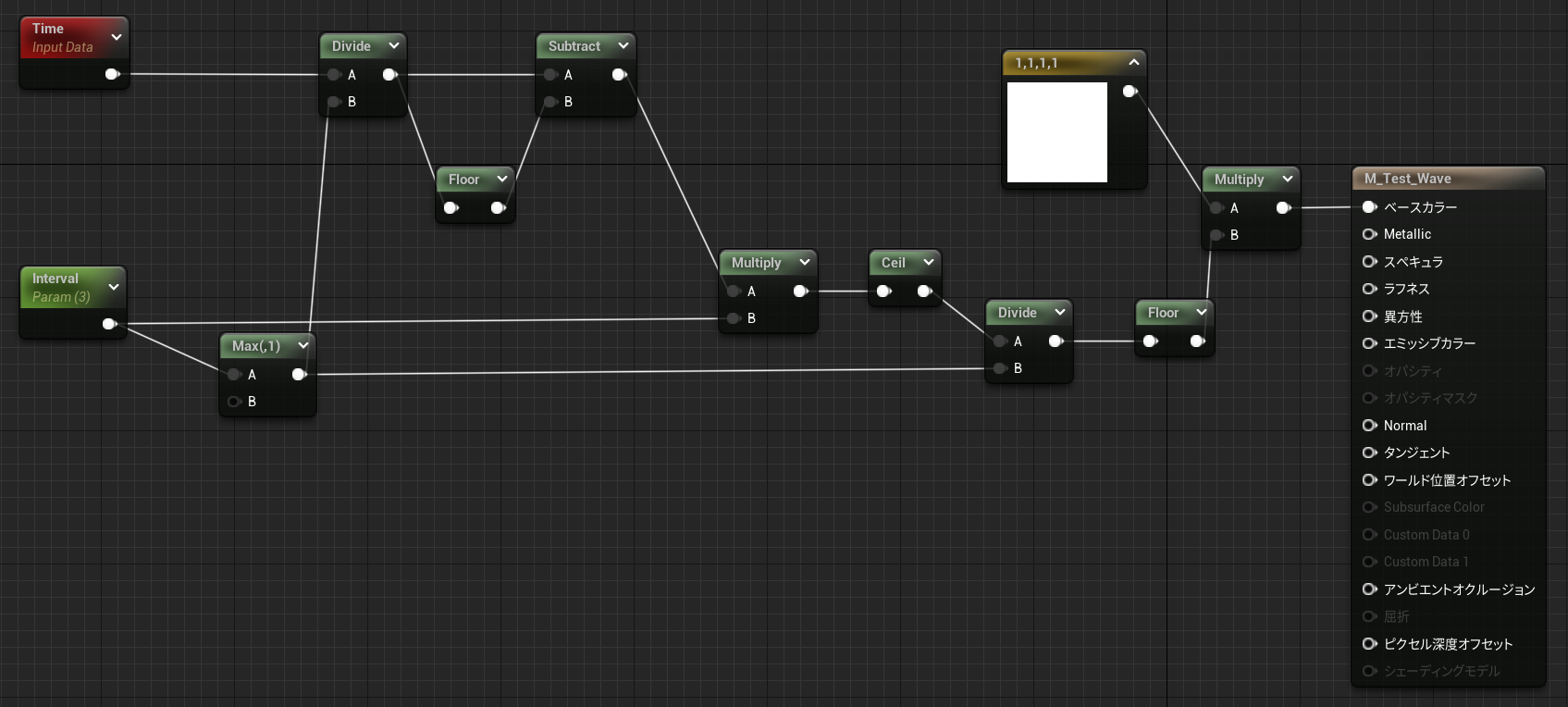
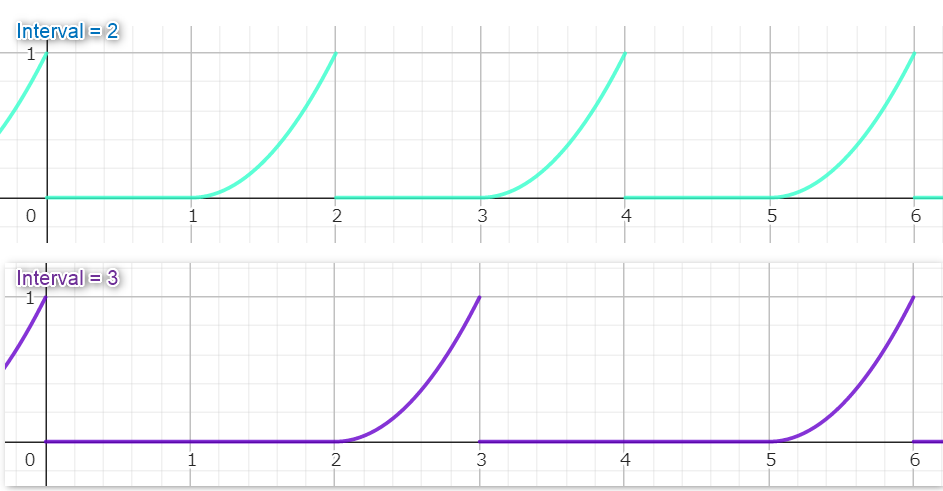
可変インターバル矩形波
設定されたIntervalの数のうち、一度のみ矩形波が立ち上がる波形。
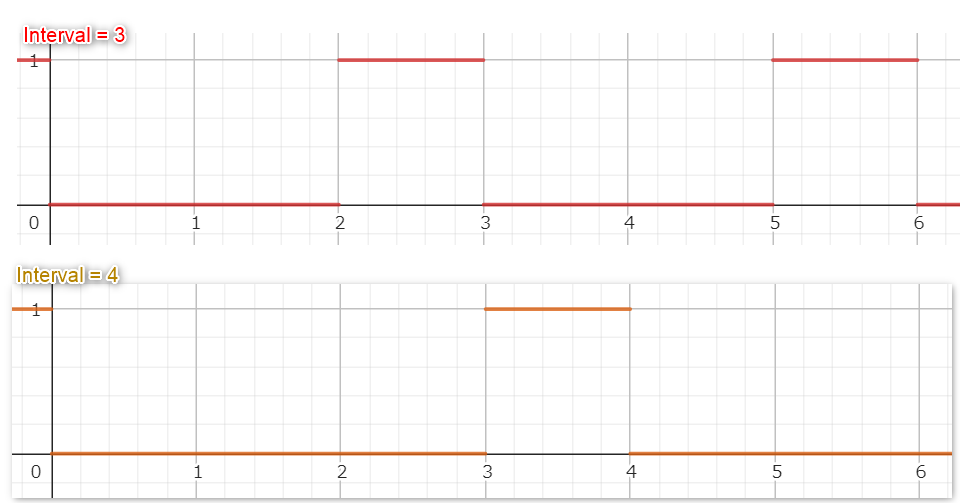
計算式
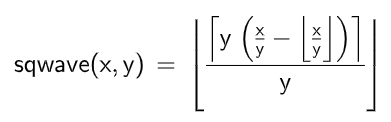
※x = 時間, y = インターバル（1.0<=yの自然数を取る）
マテリアル
※Intervalが1以下にならないように注意
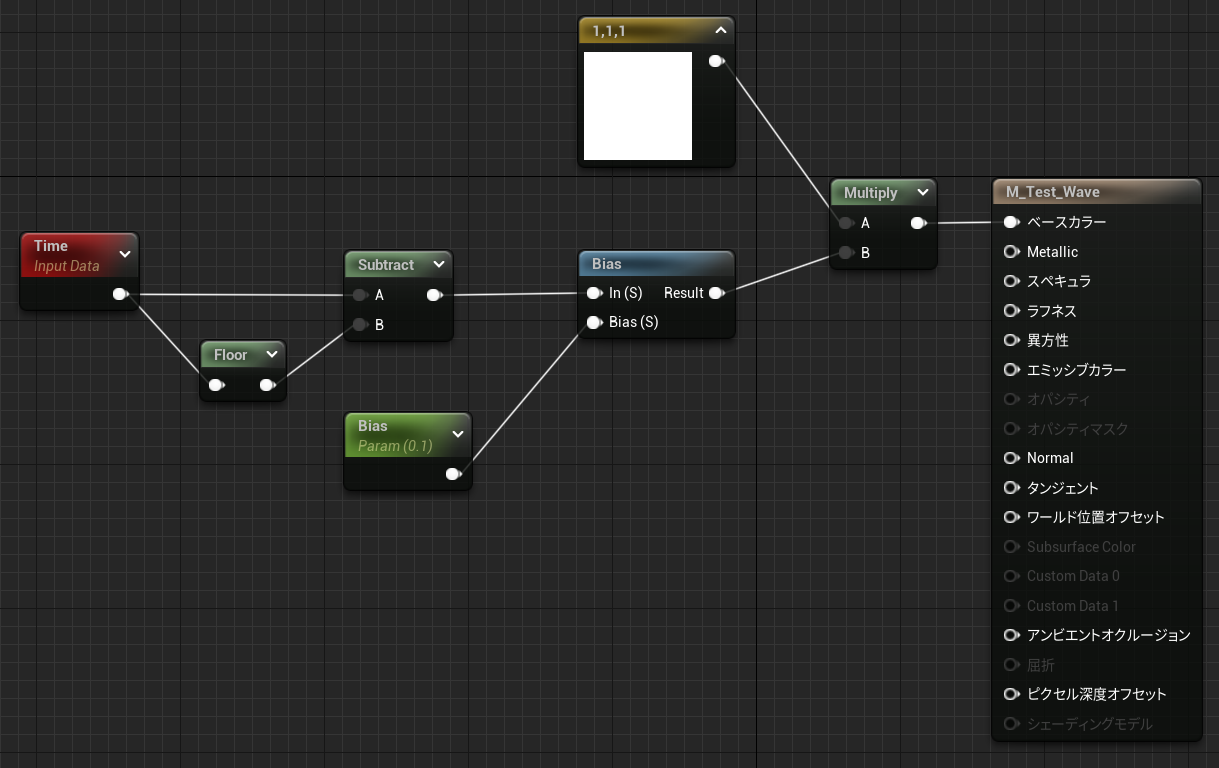
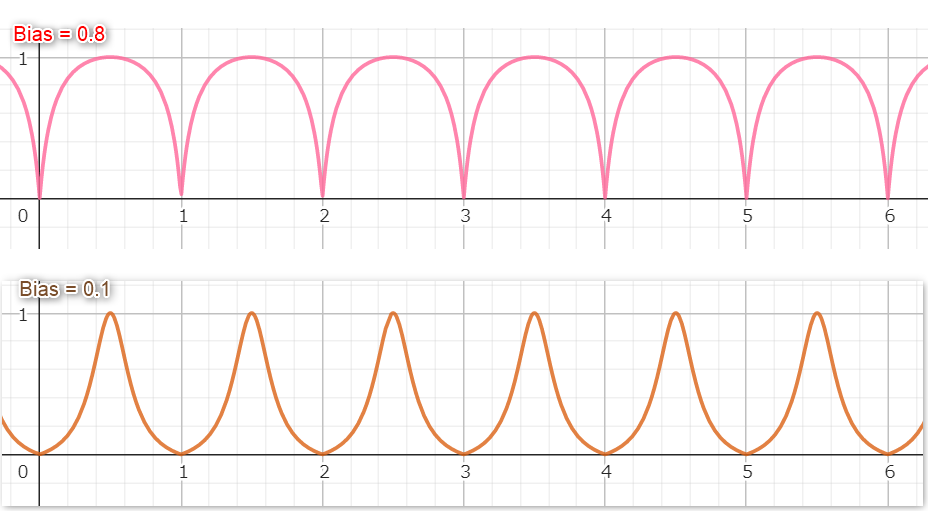
可変バイアス矩形波
反復的な波形（ここでは矩形波）に対してバイアスをかけて歪ませる。
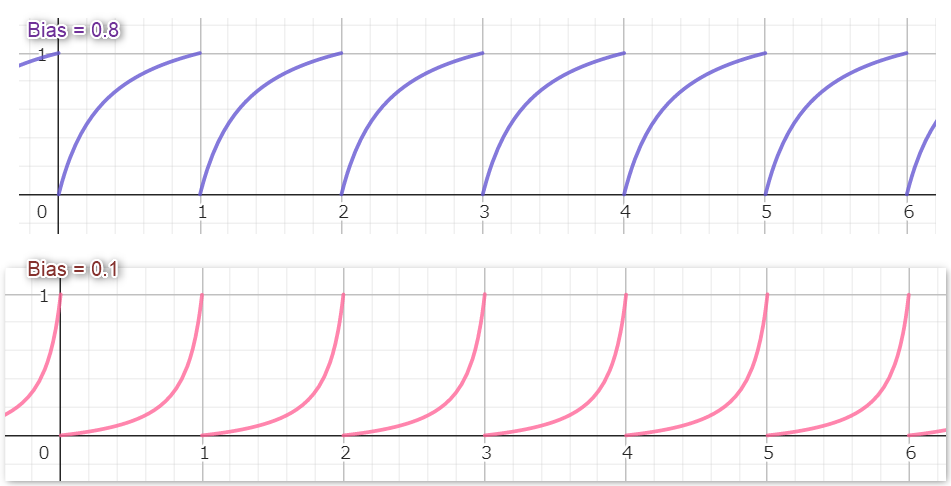
計算式
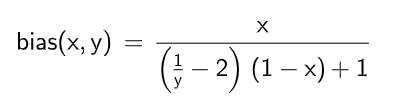
※x = 任意の波形式, y = バイアス（0.0<y<=1.0の範囲の値を取る）
マテリアル
※Biasが0にならないように注意
応用グラフ
ベースグラフと可変グラフを組み合わせることで、自由度の高い反復的なグラフを出力できる。
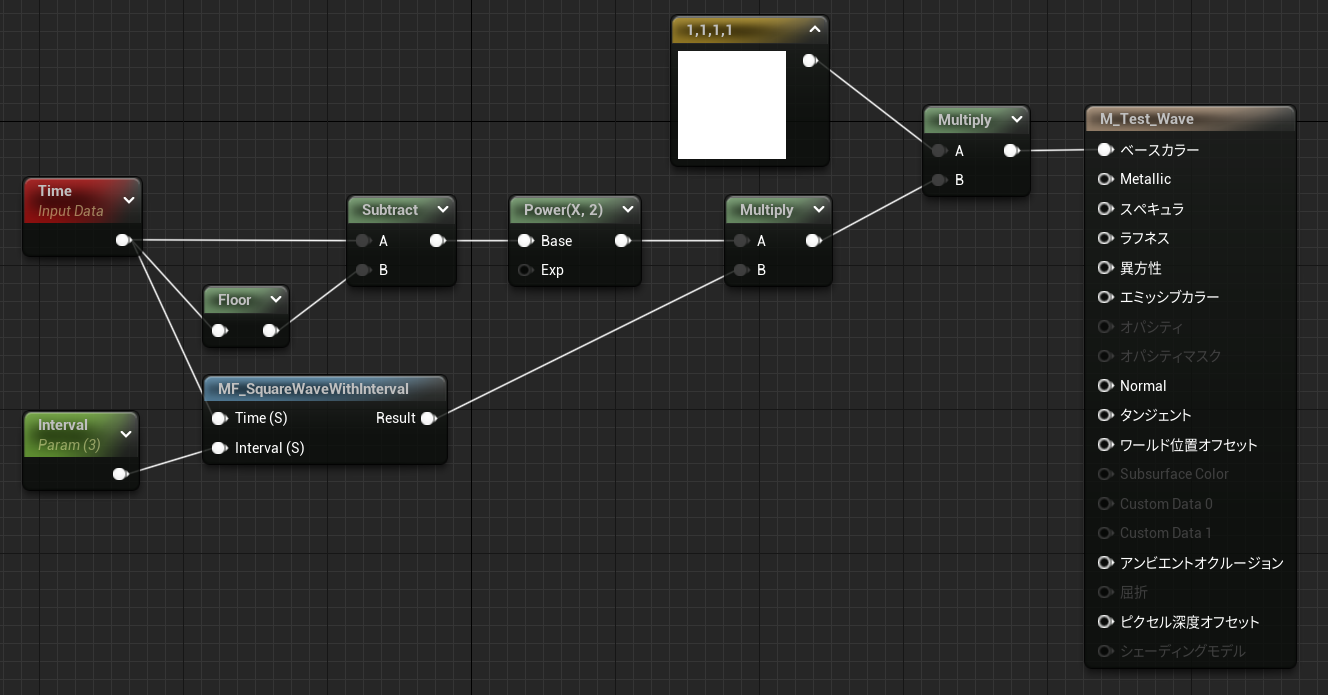
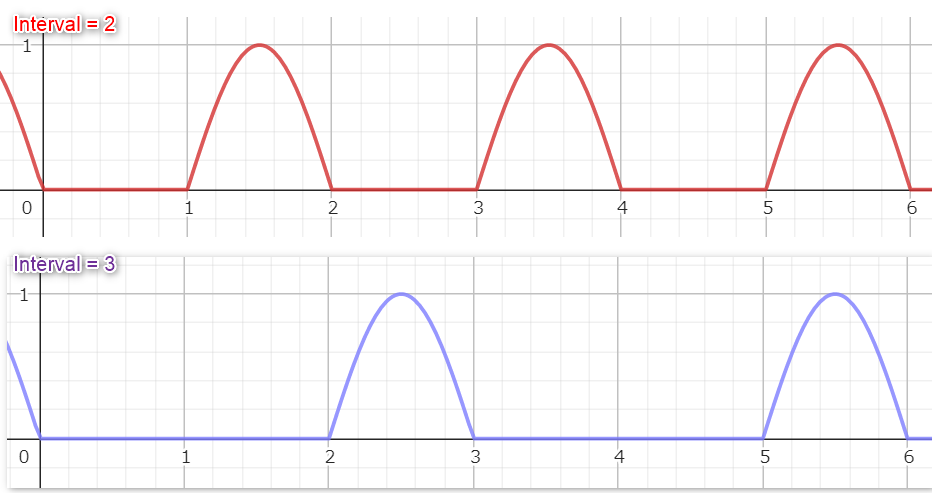
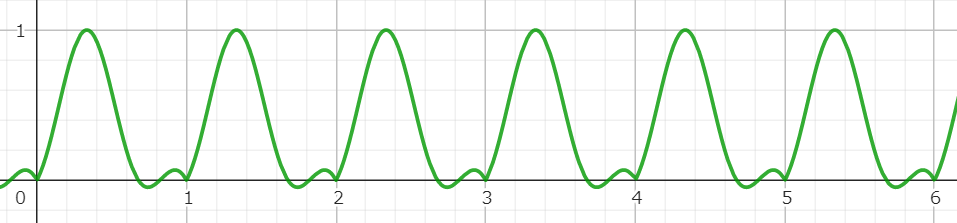
可変インターバル矩形波 + 二次曲線ノコギリ波（乗算）
マテリアル
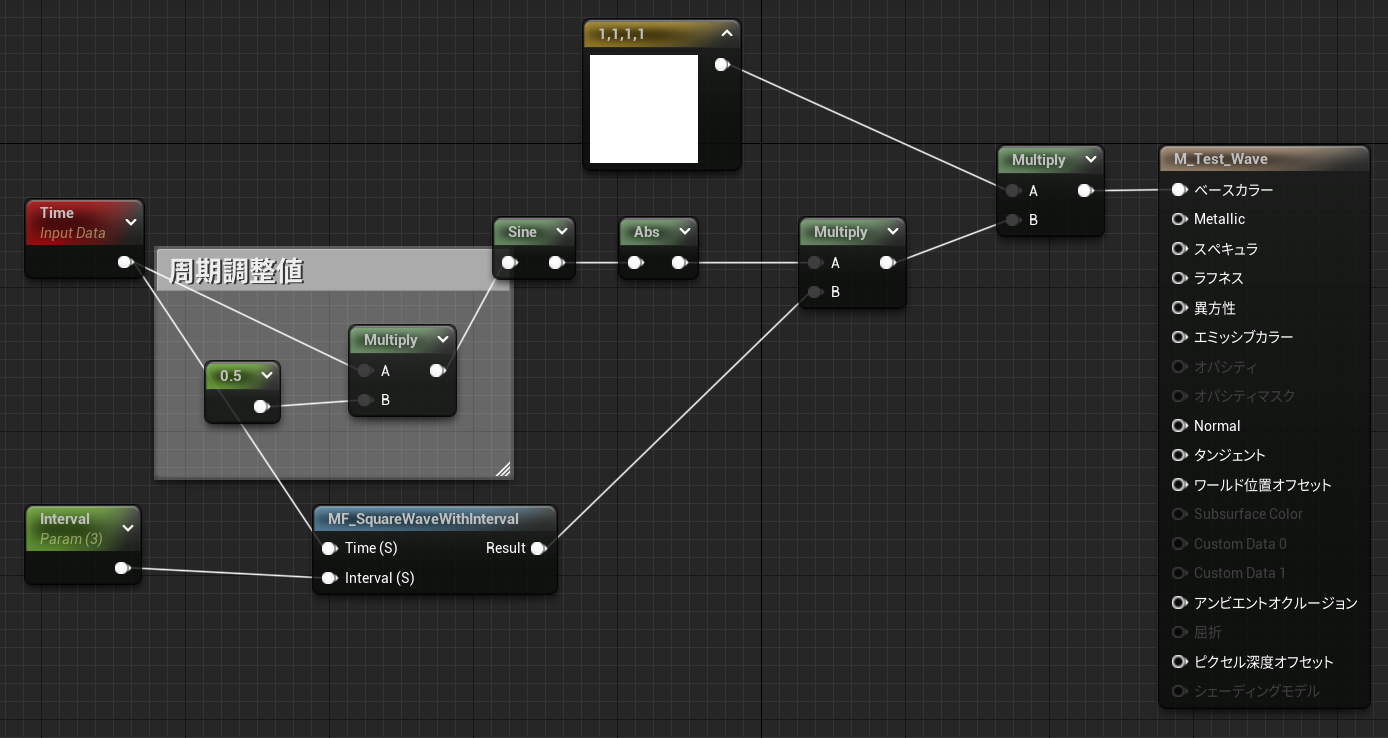
可変インターバル矩形波 + 絶対値サイン波（乗算）
マテリアル
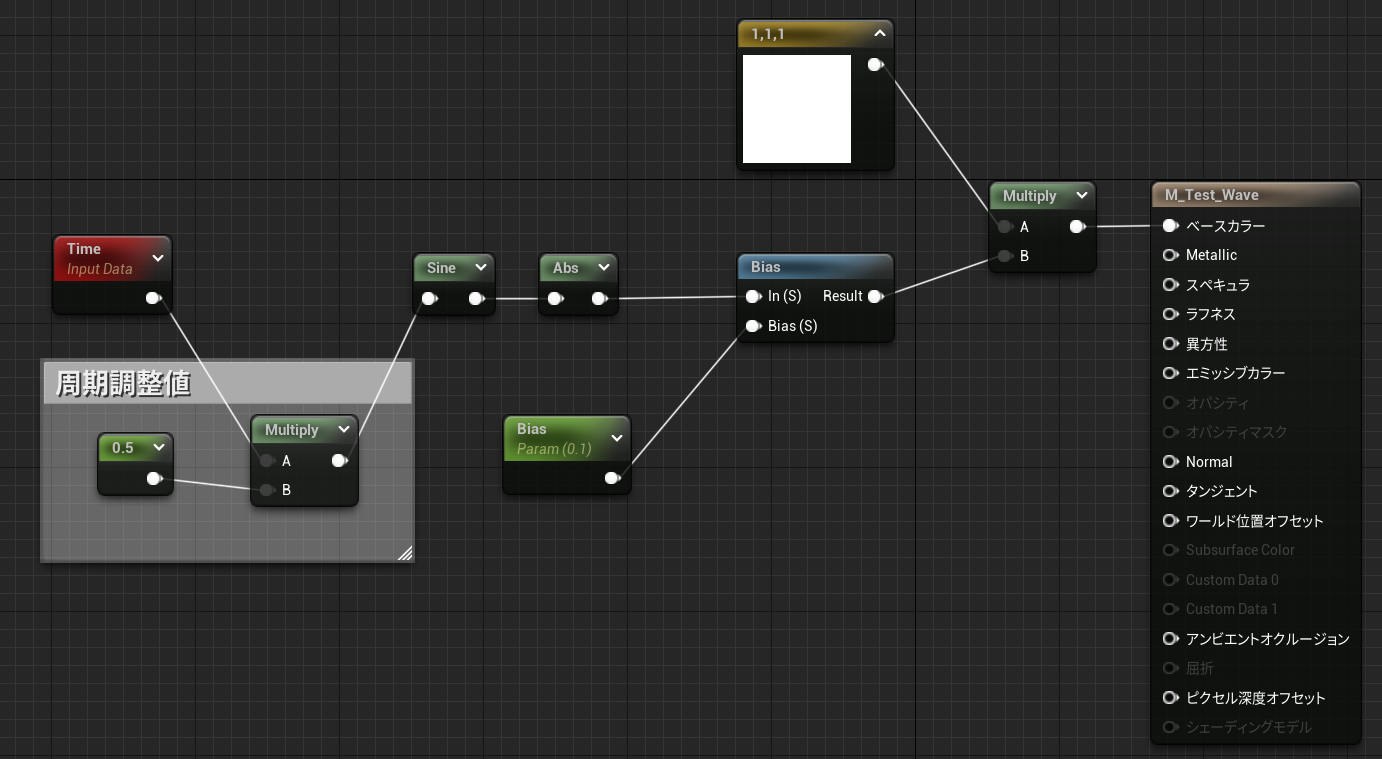
可変バイアス + 絶対値サイン波（波形変更）
マテリアル
まとめ
高校数学程度の知識は必要だが反復的な波形は簡単に作れるため是非やってみていただきたい。
おまけ
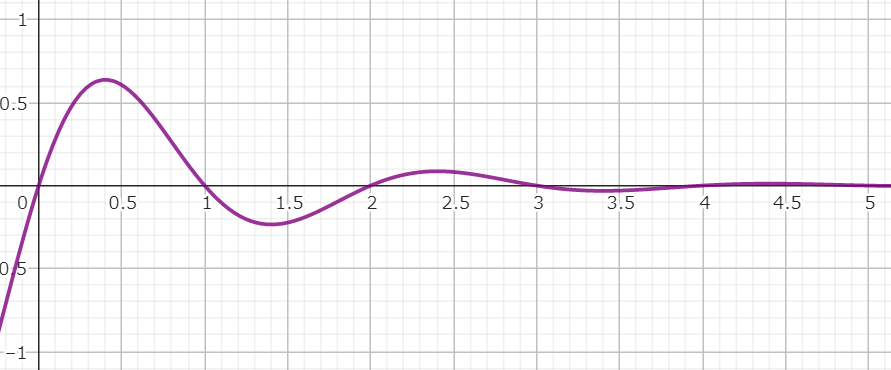
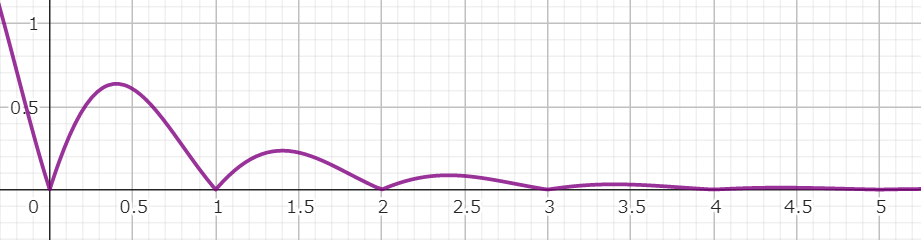
減衰波
計算式
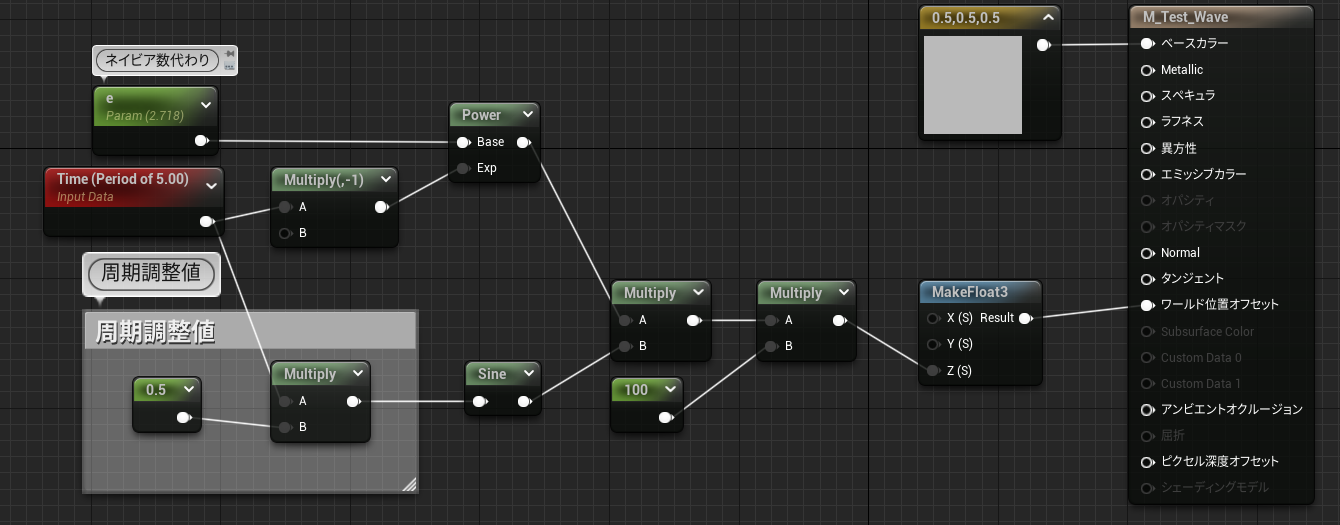
マテリアル
バウンシングボール
ボールが弾むときの軌跡も簡単につくれる。
計算式
マテリアル
なんちゃって反復減衰波
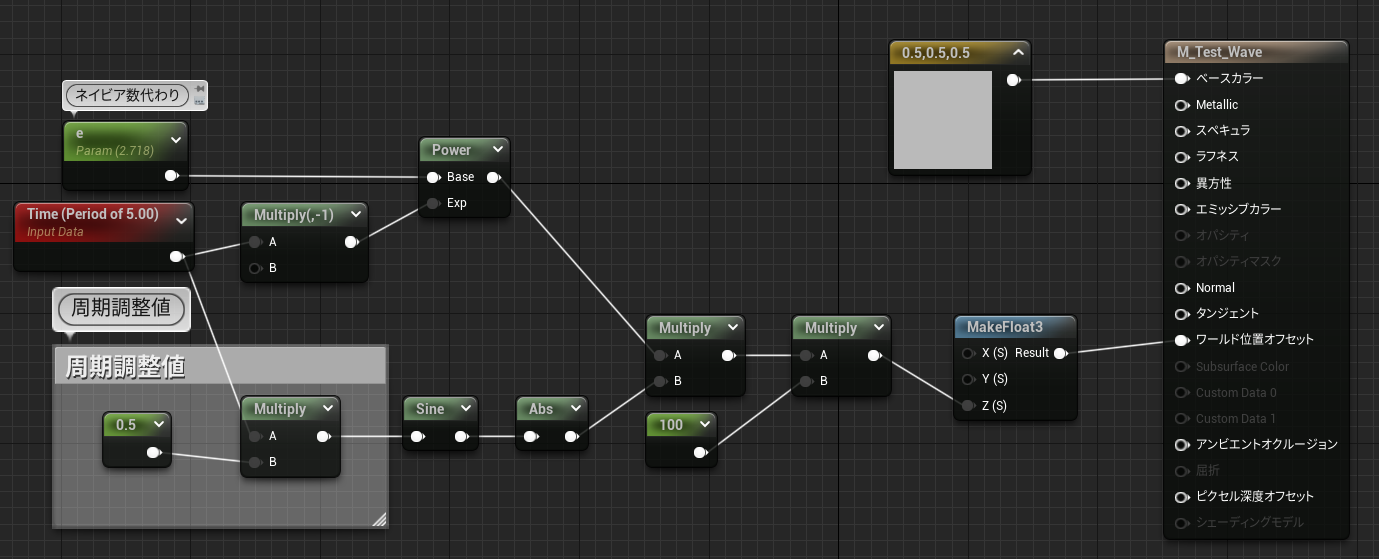
計算式
複数の式を乗算しているため、一個一個示す。
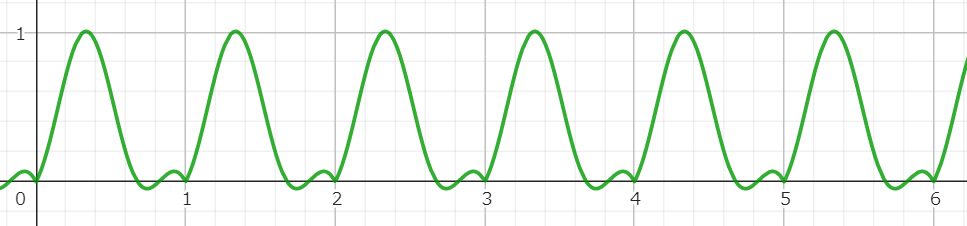
まずは周波数が2π（つまり一周期がx=0.0~1.0の間）、位相を任意定数gap分（正の値）だけずらしたグラフ。
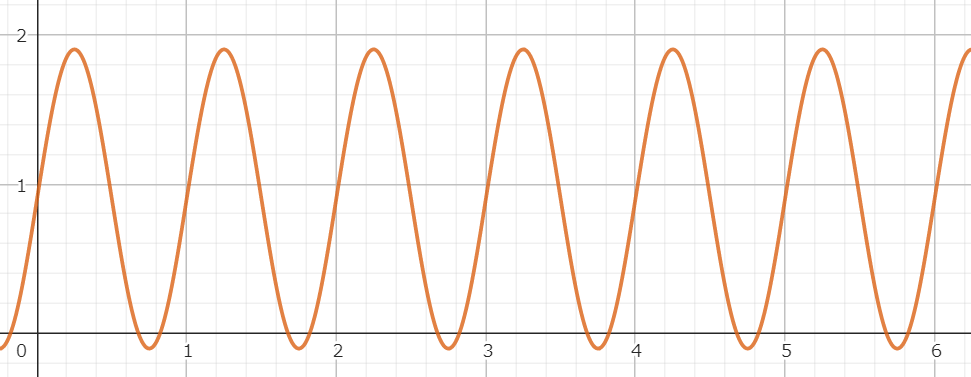
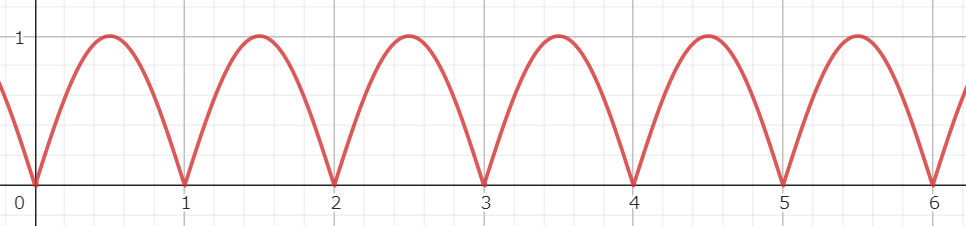
次に絶対値サイン波のグラフ。
上記二つのグラフを乗算したグラフ。
こうすることによってx=0.0~1.0の値を反復する波形を作成できる。
反復する波形は作成できたが、今のままだとyの値が1.0を越えてしまっているため、少々不都合になる場合がある。
そういった場合は任意の値でスケーリングを行う必要がある。
例えば任意定数gapの範囲を0.0~1.0に制限した場合だと次のような式を乗算することでスケーリングできる。
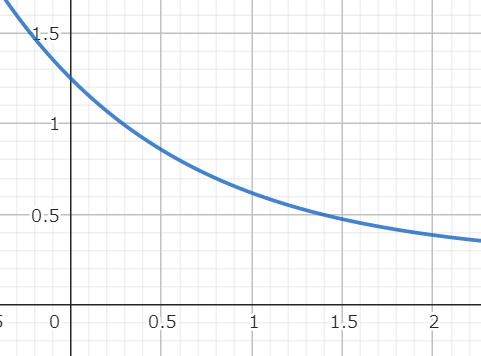
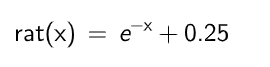
※eはネイピア数。ここへ渡すxの値は任意定数gapとする。
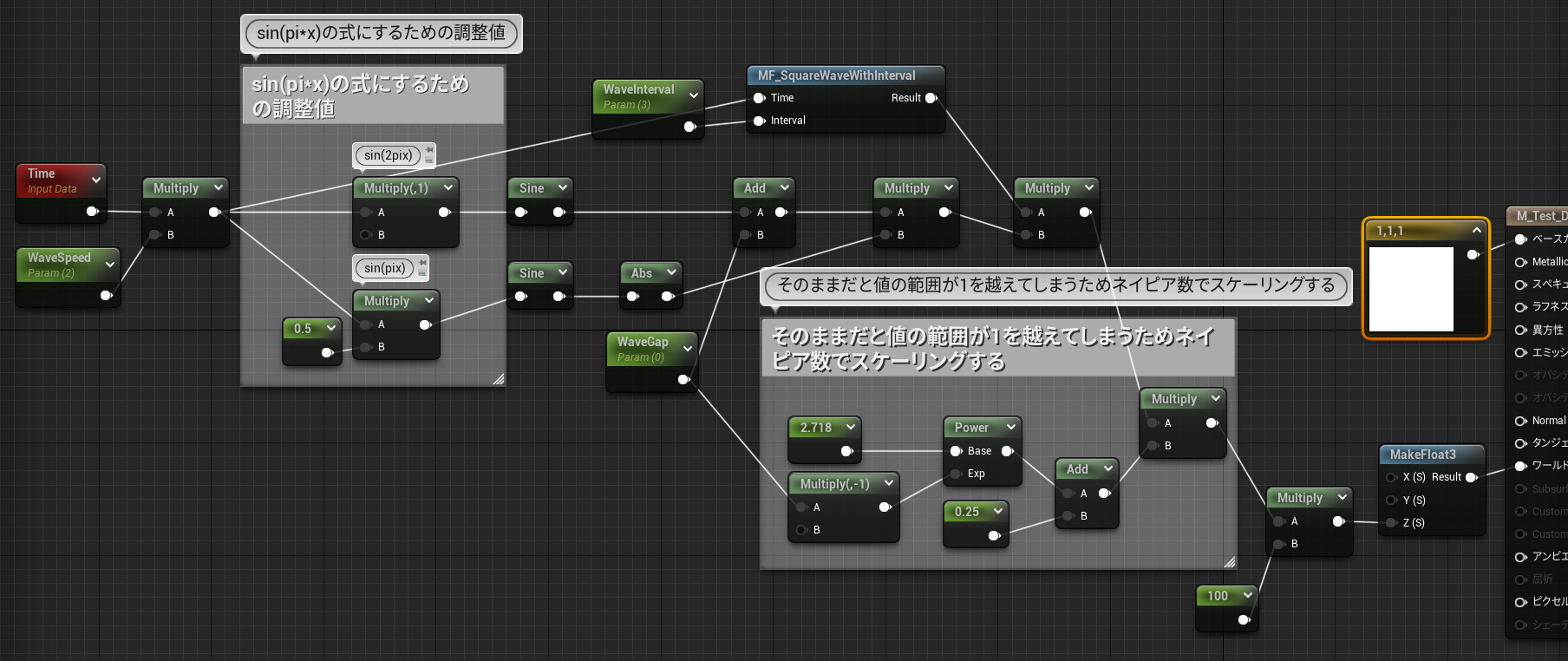
マテリアル
ちなみに
位相をずらしたサイン波の周波数を変えたり、インターバルを設けたりすると表現の幅は無限大！
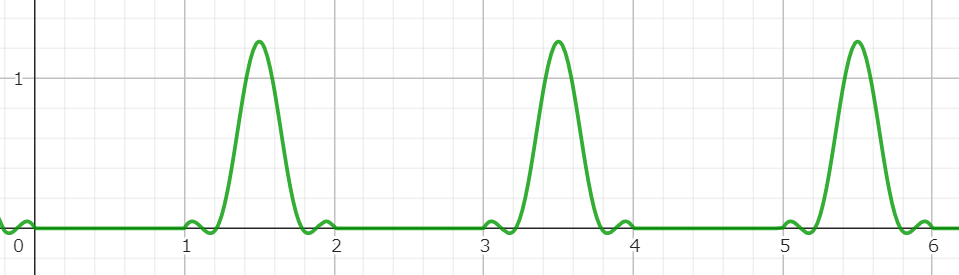
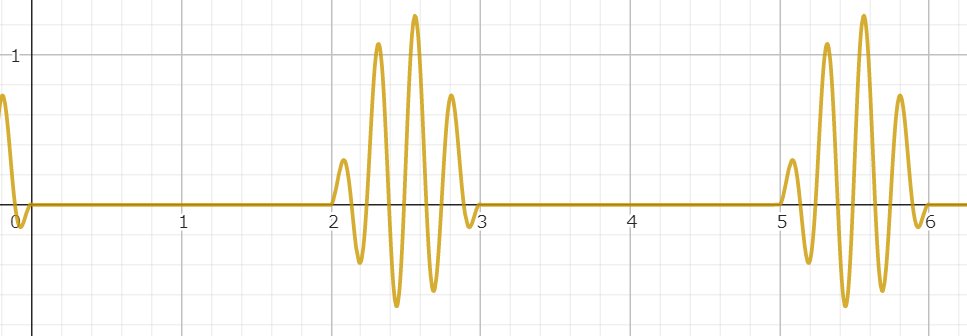
参考
・グラフ描画
https://www.geogebra.org/graphing?lang=ja
・マテリアルノード
https://docs.unrealengine.com/4.27/ja/RenderingAndGraphics/Materials/ExpressionReference/Math/