LoginSignup
2
1
@_ttt_

ニューラルネットワークで作って遊ぼう！with C language！

Last updated at Posted at 2023-11-30

この記事は SLP-KBIT AdventCalendar2023 １日目の記事です。

まえがき

こんにちは、tttです。

ということで今年も始まりました、AdventCalendar！！
去年のAdventCalendarからもう一年が経過したと考えると、時の流れは早いものです。

ここ数年、SLPのアドベントカレンダーはなかなかバトンが繋がらず、25日まで完走ができていない状況にあります。
そのうえで、バトンを繋ぐという意味を考えると初日のトップバッターを担当するというのは、かなり重要な役割を担っているのです。
去年もトップバッターを担当しましたが、初日でコケたせいで後が悲惨な状況になりました。

今年は何としてでも記事を間に合わせる、と意気込んでいるので、部員の皆さんはご安心ください。

私の記事が次の執筆者に繋がり、今年こそ25日までバトンが繋がることを祈っています。

本記事の内容

さて、今年は「ニューラルネットワーク」について記事を書きたいと思います。

「ニューラルネットワーク」と聞くと小難しく聞こえそうですが、原理はすごく単純です。
それをC言語初学者にも分かりやすく解説しようというのが本記事の趣旨になります。

「プログラミング」と「論理回路」を履修している１年生は必読です！

パーセプトロン

ニューラルネットワークを解説する前に、その起源となる「パーセプトロン」について解説します。

パーセプトロンは、

  • 複数の入力信号
  • １つの出力信号

を持つアルゴリズムです。
入力信号、出力信号は、それぞれ $0$ もしくは $1$ のみを値として取ります。

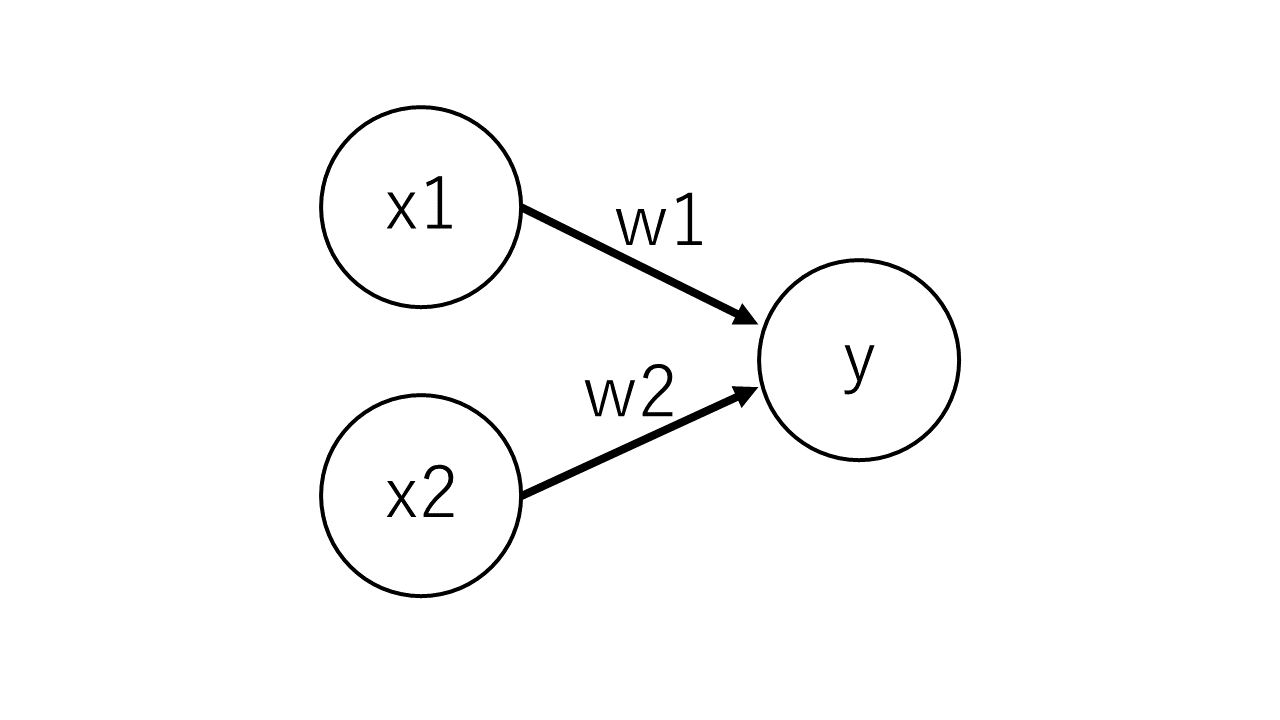
例えば、次の図は2つの信号を入力として受け取るパーセプトロンです。

perceptronEx1.png

$x_1$、$x_1$ は入力信号、$y$ は出力信号、$w_1$、$w_2$ は重みです。
「重み」とは、電流でいうところの「抵抗」であり、信号の流れにくさをコントロールするパラメータとなります。

そして、それぞれの入力信号と重みを乗算し、その総和がある限界値 $\theta$ を超えた場合のみ $1$ を出力します。

その限界値 $\theta$ を閾値と呼びます。

以上の話を数式で表現すると、次の式になります。

y=
\begin{cases}
0\quad\text{($w_1x_1+w_2x_2\leq\theta$)}\\
1\quad\text{($w_1x_1+w_2x_2>\theta$)}\\
\end{cases}

事前に $w_1$、$w_2$、$\theta$ の値を任意の値に設定しておくと、入力信号 $x_1$、$x_2$ に値が代入された場合に $y$ の値を決定することができます。

ORゲートの作成

ではこのパーセプトロンを用いてORゲートを再現する場合、$w_1$、$w_2$、$\theta$ の値をどのように設定すればよいでしょうか。

答えは無限に存在しますが、例を挙げると

(w_1,w_2,\theta)=(0.5,0.5,0.1)

とすれば良さそうですね。
実際に出力を確認すると、以下の真理値表を得ることができます。

$x_1$ $x_2$ $y$
$0$ $0$ $0$
$1$ $0$ $0$
$0$ $1$ $0$
$1$ $1$ $1$

確かにORゲートと同じです。

ではこれをC言語でプログラミングしてみましょう。

int OR(int x1, int x2) {
    double w1, w2, theta;
    w1 = 0.5;
    w2 = 0.5;
    theta = 0.1;

    double a = w1*x1 + w2*x2;
    if (a > theta) {
        return 1;
    }
    return 0;
}

OR()関数は、引数に入力信号 $x_1$、$x_2$ を持ち、戻り値に $0$ もしくは $1$ を返します。
これをmain()関数で実行します。

int main(void) {
    puts("OR");
    puts("x1 :x2 : y");
    printf(" %d : %d : %d\n", 0, 0, OR(0, 0));
    printf(" %d : %d : %d\n", 1, 0, OR(1, 0));
    printf(" %d : %d : %d\n", 0, 1, OR(0, 1));
    printf(" %d : %d : %d\n", 1, 1, OR(1, 1));
    return 0;
}

実行結果

OR
x1 :x2 : y
 0 : 0 : 0
 1 : 0 : 1
 0 : 1 : 1
 1 : 1 : 1

確かにORゲートになっています。

ANDゲート、NANDゲートの作成

ANDゲート、NANDゲートの作成は、実はパーセプトロンの構造は全く同じままで、重み、閾値を変更するだけで実行できます！

ANDゲート

重みと閾値を変更するだけなのに、ORゲートと同じアルゴリズムを用いて作成できます。

(w_1,w_2,\theta)=(0.5,0.5,0.7)

真理値表

$x_1$ $x_2$ $y$
$0$ $0$ $0$
$1$ $0$ $0$
$0$ $1$ $0$
$1$ $1$ $1$

Cプログラムで作成したAND()関数

int AND(int x1, int x2) {
    double w1, w2, theta;
    w1 = 0.5;
    w2 = 0.5;
    theta = 0.7;// 0.1 -> 0.7 に変更しただけ！

    double a = w1*x1 + w2*x2;
    if (a > theta) {
        return 1;
    }
    return 0;
}

main()関数で実行

int main(void) {
    puts("AND");
    puts("x1 :x2 : y");
    printf(" %d : %d : %d\n", 0, 0, AND(0, 0));
    printf(" %d : %d : %d\n", 1, 0, AND(1, 0));
    printf(" %d : %d : %d\n", 0, 1, AND(0, 1));
    printf(" %d : %d : %d\n", 1, 1, AND(1, 1));
    return 0;
}

実行結果

AND
x1 :x2 : y
 0 : 0 : 0
 1 : 0 : 0
 0 : 1 : 0
 1 : 1 : 1

NANDゲート

(w_1,w_2,\theta)=(-0.5,-0.5,-0.7)

真理値表

$x_1$ $x_2$ $y$
$0$ $0$ $1$
$1$ $0$ $1$
$0$ $1$ $1$
$1$ $1$ $0$

Cプログラムで作成したNAND関数

int NAND(int x1, int x2) {
    double w1, w2, theta;
    w1 = -0.5;// 0.5 -> -0.5
    w2 = -0.5;// 0.5 -> -0.5
    theta = -0.7;// 0.7 -> -0.7

    double a = w1*x1 + w2*x2;
    if (a > theta) {
        return 1;
    }
    return 0;
}

main()関数で実行

int main(void) {
    puts("NAND");
    puts("x1 :x2 : y");
    printf(" %d : %d : %d\n", 0, 0, NAND(0, 0));
    printf(" %d : %d : %d\n", 1, 0, NAND(1, 0));
    printf(" %d : %d : %d\n", 0, 1, NAND(0, 1));
    printf(" %d : %d : %d\n", 1, 1, NAND(1, 1));
    return 0;
}

実行結果

NAND
x1 :x2 : y
 0 : 0 : 1
 1 : 0 : 1
 0 : 1 : 1
 1 : 1 : 0

このように、アルゴリズム自体は変化しないのに、初期に設定する値を変化するだけで、全く異なる振る舞いを行うのがパーセプトロンの特徴です。

コラム

アルゴリズムがそれぞれのゲートで全く同じ（変化しない）ので、それ専用の関数を用意し、重みと閾値の値だけそれぞれの関数で変化させるようにするとなお良いです。

int perceptron(double w1, double w2, double theta, int x1, int x2) {
   double a = w1*x1 + w2*x2;
   if (a > theta) {
       return 1;
   }
   return 0;
}

int OR(int x1, int x2) {
   return perceptron(0.5, 0.5, 0.1, x1, x2);
}

int AND(int x1, int x2) {
   return perceptron(0.5, 0.5, 0.7, x1, x2);
}

int NAND(int x1, int x2) {
   return perceptron(-0.5, -0.5, -0.7, x1, x2);
}

XORゲートの作成

では先ほどと同様に、XORゲートを再現するような $w_1$、$w_2$、$\theta$ の組み合わせを考えて下さい。

XORゲートの真理値表

$x_1$ $x_2$ $y$
$0$ $0$ $0$
$1$ $0$ $1$
$0$ $1$ $1$
$1$ $1$ $0$






見つかりました？

実はこの真理値表を満たす組み合わせは、いくら探しても見つかりません。

なぜそのことがいえるのでしょうか。

それは、先ほどの式

y=
\begin{cases}
0\quad\text{($w_1x_1+w_2x_2\leq\theta$)}\\
1\quad\text{($w_1x_1+w_2x_2>\theta$)}\\
\end{cases}

を $x_1$ と $x_2$ に関する式に変更することで分かります。
$y=0$ の場合で考えましょう。

その時の式は

w_1x_1+w_2x_2\leq\theta

で表されるので、これを式変形すると、

x_2\leq-\dfrac{w_1}{w_2}x_1+\dfrac{\theta}{w_2}

になります。
$w_1$、$w_2$、$\theta$ はそれぞれ定数なので、この式は更に

x_2\leq-ax_1+b

というシンプルな形に直すことができます。
この式は直線を表す1次関数です。

例えば、ORゲートを表すパラメータ

(w_1,w_2,\theta)=(0.5,0.5,0.1)

を上式に代入すると、

x_2\leq-x_1+0.5

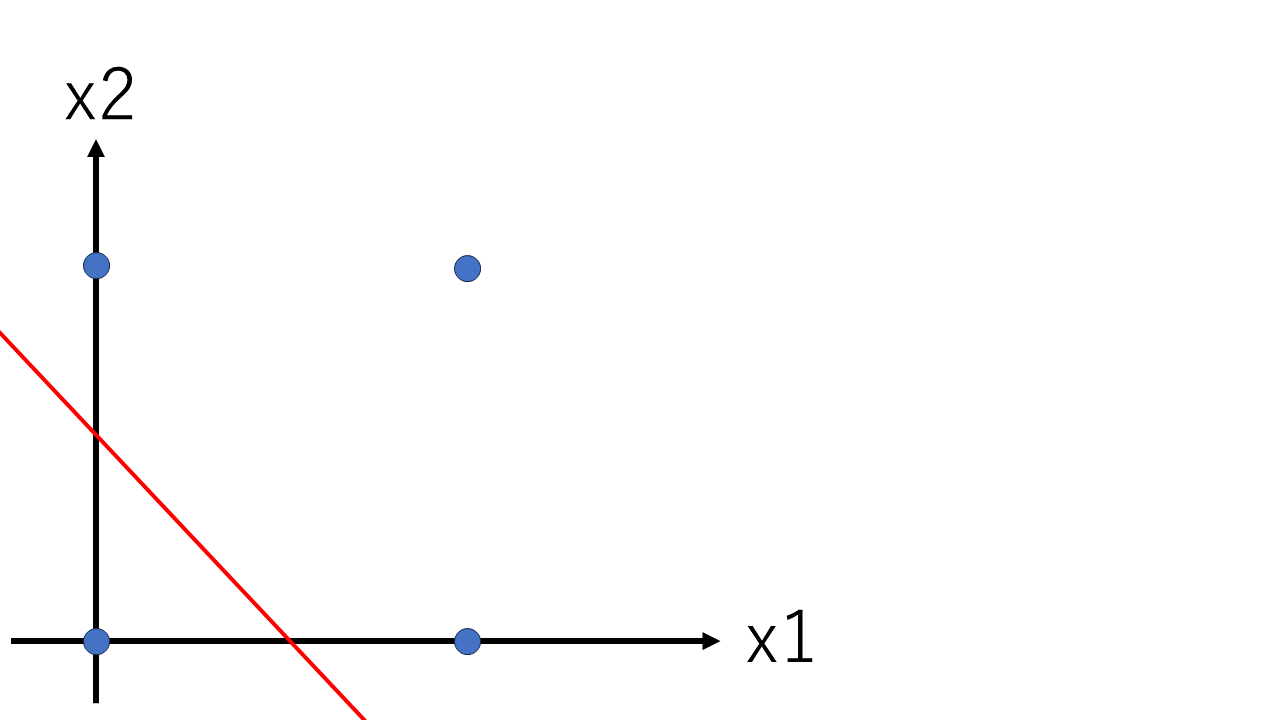
が得られ、グラフとして可視化すると次の図のようになります。

graphEx1.png

x_2\leq-\dfrac{w_1}{w_2}x_1+\dfrac{\theta}{w_2}

は $y=0$ の場合と前提しているので、つまりこのグラフの下側が $y=0$ の領域、グラフの上側が $y=1$ の領域を表しており、確かにORゲートの入力信号と出力信号が一致します。

つまりパーセプトロンを用いてゲートを再現するという事は、直線を利用して領域を分割する行為に等しいと言えます。

ここでXORゲートの話に戻ります。

先ほどのORゲート同様に、$(x_1,x_2)=(1,0),(0,1)$ の時は $y=0$ 、$(x_1,x_2)=(0,0),(1,1)$ の時は $y=1$ となるような直線の引き方を考えます。

そのような直線の引き方が物理的にできないことに気付くはずです。

これがパーセプトロンを用いてXORゲートを実現できない理由になります。

パーセプトロンの限界

ではパーセプトロンを用いてXORゲートを再現することはできないのでしょうか。

実はある工夫を施すことで、パーセプトロンでもXORゲートを作成することが可能です。

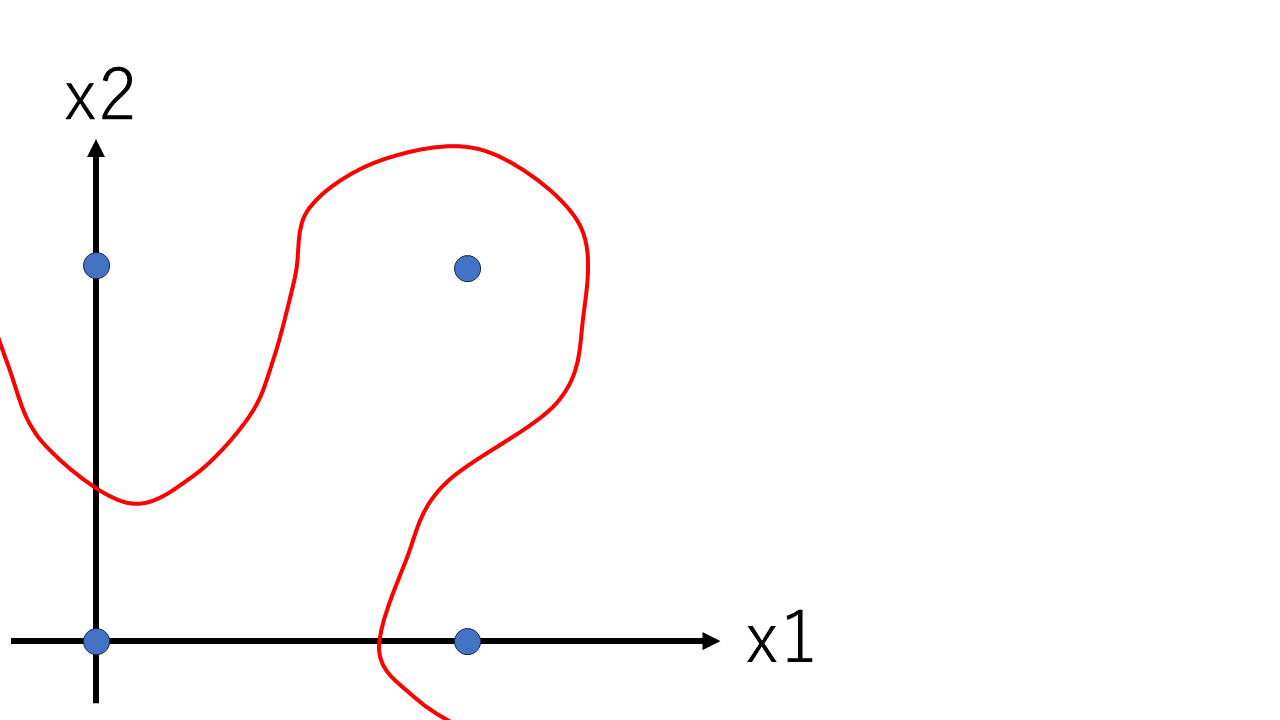
先ほどまで直線を利用した領域の分割を考えていましたが、「直線」という制約を外すと、$y=0$ と $y=1$ の領域は次の図のように分割できます。

graphEx2.png

ではこのように曲線を表すグラフをパーセプトロンでどのように再現すれば良いのでしょうか。
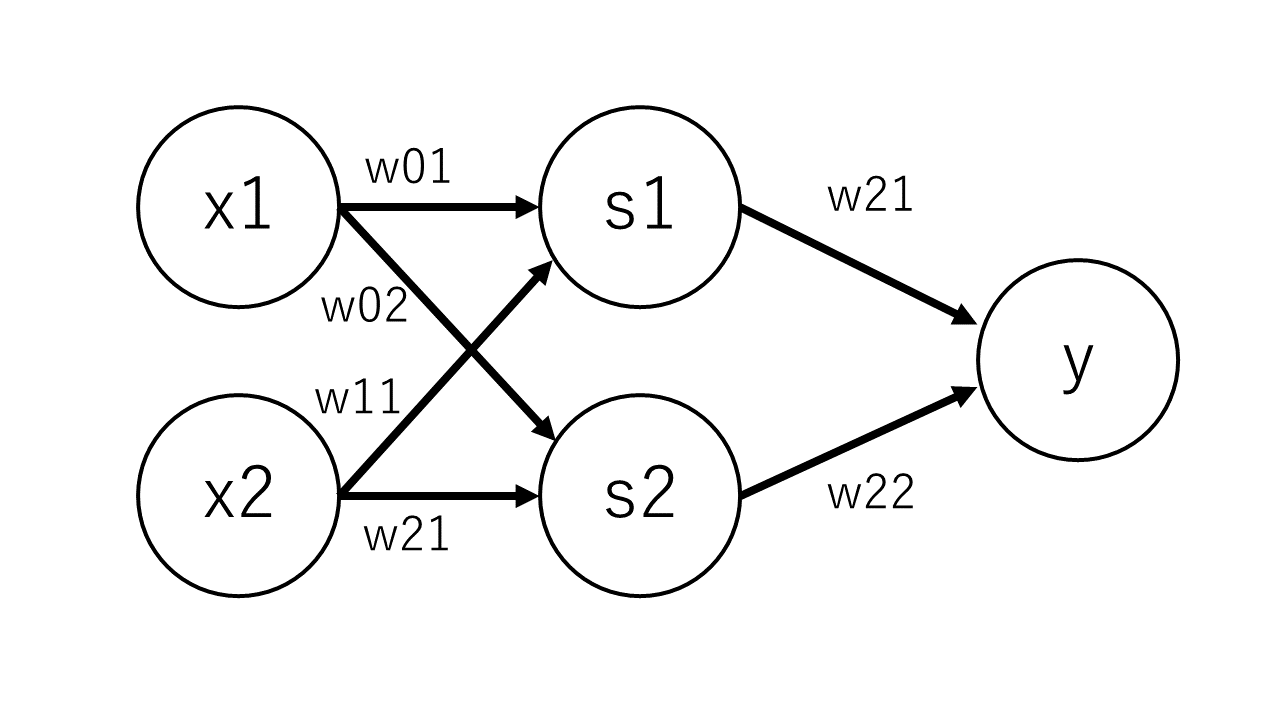
それは、パーセプトロンの層を増やすことで実現できます。

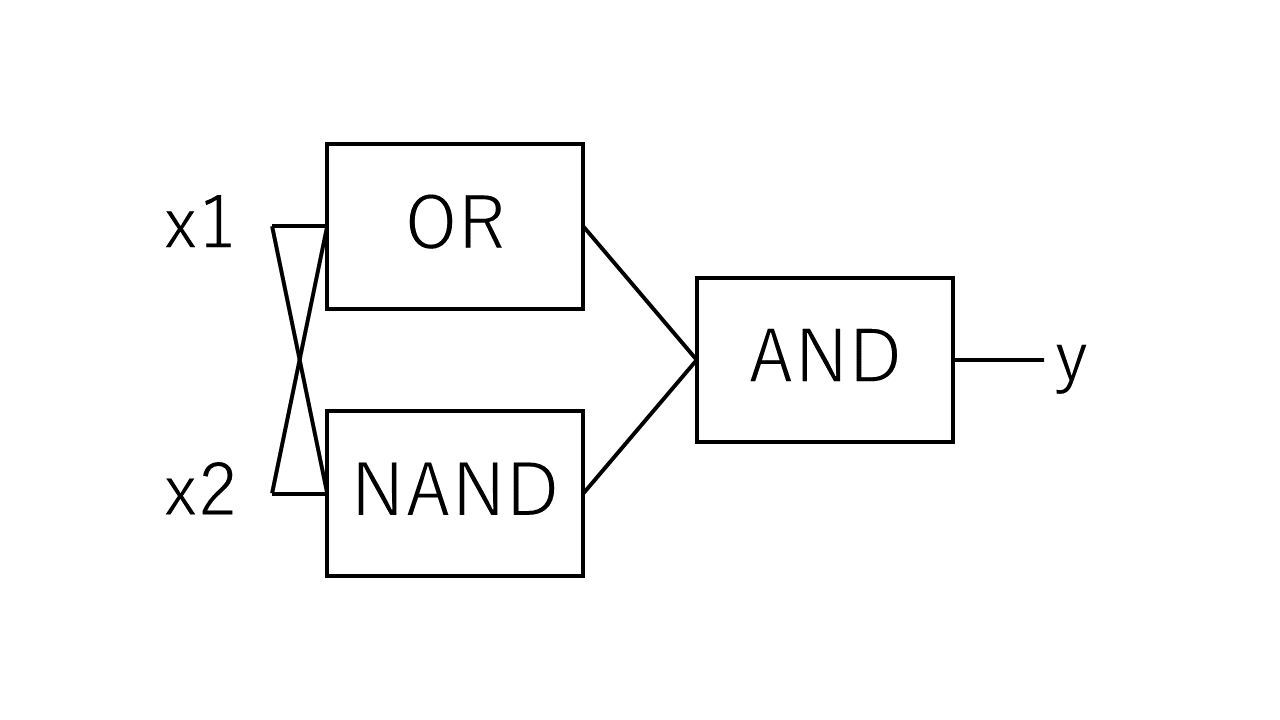
XORゲートは、ANDゲートとORゲートとNANDゲートを組み合わせることで作成できることが知られています。
そのことを利用して、パーセプトロンで得た出力を新たな入力とし、次のパーセプトロンへ情報を伝達することで、複雑な問題を解決することができるのです。

このような複数の層を持つパーセプトロンを多層パーセプトロンと呼びます。

xorEx01.png
XORゲートを再現する回路図

xorEx02.png
多層パーセプトロンの図

Cプログラムで作成したXOR()関数

#include <stdio.h>
int perceptron(double w1, double w2, double theta, int x1, int x2) {
    double a = w1*x1 + w2*x2;
    if (a > theta) {
        return 1;
    }
    return 0;
}

int OR(int x1, int x2) {
    return perceptron(0.5, 0.5, 0.1, x1, x2);
}

int AND(int x1, int x2) {
    return perceptron(0.5, 0.5, 0.7, x1, x2);
}

int NAND(int x1, int x2) {
    return perceptron(-0.5, -0.5, -0.7, x1, x2);
}

int XOR(int x1, int x2) {
    return AND(OR(x1, x2), NAND(x1, x2));
}

int main(void) {
    puts("XOR");
    puts("x1 :x2 : y");
    printf(" %d : %d : %d\n", 0, 0, XOR(0, 0));
    printf(" %d : %d : %d\n", 1, 0, XOR(1, 0));
    printf(" %d : %d : %d\n", 0, 1, XOR(0, 1));
    printf(" %d : %d : %d\n", 1, 1, XOR(1, 1));
    return 0;
}

実行結果

XOR
x1 :x2 : y
 0 : 0 : 0
 1 : 0 : 1
 0 : 1 : 1
 1 : 1 : 0

ニューラルネットワーク

いよいよニューラルネットワークの解説に入ります。

$\cdots$と、行きたいところですが、長くなったので執筆はここまで
タイトル詐欺とかいわないで

一応、ニューラルネットワークを搭載した面白いシステムは作成したのですが、その解説をするとなると軽く1000行は超えてしまいそうな勢いなんですよ$\cdots$（現在384行。これまでした解説の倍はかかりそう）。

堪忍な。

SLPメンバーは数カ月するとそれについて私が書いた記事が読めるので、
しばし待たれよ。

中途半端なおわりになりますが、一旦ここで説明は以上とさせていただきます。
気が向いたらまた続きを書きます。

ではまた12月24日の記事で。

前の日の記事：
なし

次の日（２日目）の記事：
https://qiita.com/nagotta/private/324cf7a9c585e5b3a369

編集

2023.12.01-14:23
OR()関数の誤りを訂正

2023.12.05-15:15
他の日付を担当している人のリンクを追加

参考

ゼロから作るDeep Learning
―Pythonで学ぶディープラーニングの理論と実装
斎藤 康毅　著
オライリー・ジャパン発行

公式サイト

2
1
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
2
1