概要
競馬の入着確率予測モデルの出力とオッズを基に、数理最適化による購入馬券の最適化を行います。
この記事では主に最適化部分についての説明と実装を紹介するとともに、実際に学習した予測モデルを使って最適化結果の馬券を購入し、12月18日、12月19日のレースでは収支プラスを達成しました。
最適化手法については以下の論文を参考にしています。
Optimal sports betting strategies in practice: an experimental review
はじめに
去年のAdbent Calendarでは、RankNetを使った競馬予測モデルの作成についての記事を書きました。
TensorFlowでRankNetを実装して、競馬の着順予測モデルを作りました。
これを使って約1年間賭け続けましたが、結果として収支はマイナスになってしまいました。
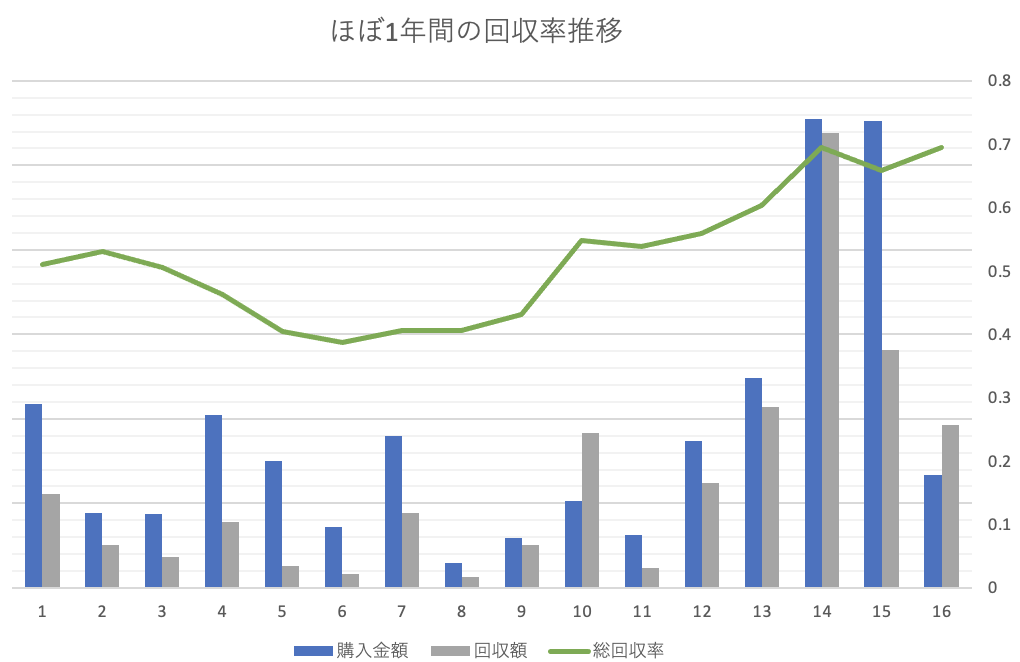
モデルの予測精度が問題であるという見方もできますが、もう一つ要因と考えられるのが、購入馬券が適切でないことです。
前回紹介したモデルでは、「入力値(該当レースにおける該当馬)に対する出力値が高いほど、そのレースにおいて有力である」といった予測結果を得ることができます。しかし、その結果に対してどの馬券をいくら買うかに関しては私(ほぼ初心者)が考えて決めています。
予測結果に基づいて、利益が大きく、リスクの小さい馬券購入を行うことができれば、収支も改善すると考えられます。
話は変わって、ポートフォリオ最適化問題と呼ばれる組み合わせ最適化問題の代表的な1つがあります。
主に、収益率の異なる投資先が複数ある場合に、手持ちの資産をどのように分散投資することでリスクを最小化できるかを解く問題になります。
収益率の異なる投資先(各馬券種)、手持ちの資産(賭け金)、分散投資(馬券の購入)のように置き換えると馬券購入に対しても適用可能のように思えます。
そこで、ポートフォリオ最適化問題の枠組みで購入馬券の最適化を行うことにしました。
最適化手法
以下の論文で紹介されているSharpe Strategyをベースとしています。
Optimal sports betting strategies in practice: an experimental review
定義
最適化対象である最適化パラメータは、どの馬券にいくら賭けるかという戦略$\mathbf{f}$とします。
${\mathbf{f}}$は、その馬券が的中する確率$\mathbf{p}$とその馬券のオッズ$\mathbf{o}$をパラメータとして決定されます。
しかし、真の的中確率$\mathbf{p}$は分からないため、予測モデルなどで推定した的中確率$\mathbf{\hat{p}}$で代替します。
g: (\mathbf{\hat{p}}, \mathbf{o}) \mapsto \mathbf{f}
また、これにより得られる報酬を$\mathbf{r}$とします。これらは対象馬券ごとに設定されます。
\mathbf{f} = [f_1, f_2, f_3, ..., f_n] \\
\mathbf{p} = [p_1, p_2, p_3, ..., p_n] \\
\mathbf{o} = [o_1, o_2, o_3, ..., o_n] \\
オッズ行列
ここで各オッズを並べた行列であるオッズ行列を作成します。
\mathbf{O} = [\mathbf{o_1}, \mathbf{o_2}, \mathbf{o_3}, ..., \mathbf{o_n}, \mathbf{c}] \\
$\mathbf{o_i}$はそれぞれの馬券を購入した際に得られるオッズベクトルになっています。競馬においては馬券が的中したとき以外はオッズは0であるため、該当馬券のインデックスに馬券のオッズが入り、それ以外は0のone-hotベクトルになります。
また、新たに追加した$\mathbf{c}$は馬券を購入しないという選択肢を追加しています。この選択肢を選んだ場合は、どの馬券が的中しようと馬券購入しなかった分だけ返ってくるため、全要素が1のベクトルになります。
\mathbf{o_i} = [o_{i1}, o_{i2}, o_{i2}, ..., o_{in}]^T$ \\
\mathbf{c} = [1, 1, 1, ..., 1]^T$ \\
ここでオッズ行列を簡単にするため、ここで賭けた分が返ってくる分、購入しなかった分を取り除いた$\mathbf{\rho}$を用意します。
\mathbf{\rho} = \mathbf{O} - \mathbf{1}
Modern Portfolio Theory
Modern Portfolio Theory(MPT)は報酬の期待値と分散を最適化対象とする一般的な最適化手法の一つです。
ある投資戦略$\mathbf{f}$と$\mathbf{\rho}$を掛け合わせることで得られる報酬の期待値が計算できます。異なる投資戦略$\mathbf{f_1}, \mathbf{f_2}$を考えます。それらで期待値を計算して以下のような関係である場合には$\mathbf{f_1}$の方が期待値が高く、優れた戦略だといえます。
\mathbb{E}[\mathbf{\rho}・\mathbf{f_1}] > \mathbb{E}[\mathbf{\rho}・\mathbf{f_2}]
また、一方でリスクが低い戦略の方が望ましいという考えもあります。MPTではリスクを分散と考えます。
期待値と同様にそれらで分散を計算します。以下のような関係である場合には$\mathbf{f_2}$の方が分散が小さく、優れた戦略だといえます。ここで$\Sigma$は$\mathbf{\rho}$の共分散行列です。
\mathbf{f_1}^T \Sigma \mathbf{f_1} > \mathbf{f_2}^T \Sigma \mathbf{f_2}
これらの期待値とリスク(分散)のバランスをとりながら最適化を行うため、以下のような目的関数、制約式に従って、最適化を行う手法がMPTです。$\gamma$は定数であり、リスクをどれだけ重視するかを決めるパラメータになります。
Maximize: \mathbb{E}[\mathbf{\rho}・\mathbf{f}] - \gamma \mathbf{f}^T \Sigma \mathbf{f} \\
Subject\ to\ \sum_{i=0}^{n} f_i = 1, f_i \ge 1
Maximum Sharpe Strategy
MPTではパラメータ\gammaがあり、これをどの程度設定するかによって投資戦略$\mathbf{f}$は変わってしまいます。
この問題を解決する手法の1つは、期待値とリスクのパレートフロントの中で、最も利益を得られる投資戦略を選ぶことです。
Sharpe Ratioと呼ばれる「リスクあたりの利益」を計算する式があり、以下の通りです。
$\mathbb{E}(w)$は収益wの期待値, $sigma(w)$はwの標準偏差(リスク)、$r$は投資しないことによって得られる収益です。
\frac{\mathbb{E}(w) - r}{\sigma(w)}
Sharpe Ratioの形にMPTを合わせると以下のような最適化式になります。
これがMaximum Sharpe Strategyとなります。
Maximize: \frac{\mathbb{E}[\mathbf{\rho}・\mathbf{f}]}{\sqrt{\mathbf{f}^T \Sigma \mathbf{f}}} \\
Subject\ to\ \sum_{i=0}^{n} f_i = 1, f_i \ge 1
これに対して、予測モデルから計算される馬券的中確率$\mathbf{p} = [p_1, p_2, p_3, ..., p_n, 1]$をオッズ行列にかけた以下の最適化式で、予測モデルの結果を反映した馬券最適化を行います。
Maximize: \frac{\mathbb{E}[\mathbf{p}\mathbf{\rho}・\mathbf{f}]}{\sqrt{\mathbf{f}^T \Sigma \mathbf{f}}} \\
Subject\ to\ \sum_{i=0}^{n} f_i = 1, f_i \ge 1
実装
pythonの線形計画問題の最適化記述ライブラリであるscipy.optimizeを使って実装します。
scipyはpipでインストール可能です。
import scipy.optimize as sco
def sharpe_optimize(odds, pred, index, budget=1000):
"""Sharpe Strategyによる最適化を行う
Args:
odds (numpy.array): オッズ
pred (numpy.array): 馬券の的中確率
index (list): 馬券の名前
budget (int): 投資予算
Return:
boolean: 最適解が得られたらTrueを返す
pandas.DataFrame: 最適化結果を含むデータフレーム
"""
def problem_func(weights, odds_matrix, pred):
"""目的関数
Args:
weights (numpy.array): 分配比率(最適化パラメータ対象)
odds_matrix (numpy.array): オッズ行列
Return:
float: 最適化する目的値
"""
return -(pred * np.dot(odds_matrix, weights)).mean() / np.sqrt(np.cov(np.dot(odds_matrix, weights)))
odds_matrix = np.concatenate((np.diag(odds), np.ones((len(odds), 1))), axis=1)- 1
odds = np.concatenate((odds, np.ones(1)), axis=0)
# 初期解
x0 = np.ones(len(odds)) / len(odds)
# 制約条件
constraints = [{"type": "eq", "fun": lambda x: np.sum(x) - 1}]
# 上下制約
bounds = [(0, None)] * len(odds)
# 最適化
opts = sco.minimize(fun=problem_func, x0=x0, args=(odds_matrix, pred), method="SLSQP", bounds=bounds, constraints=constraints)
# 表示用のデータフレームを作成
df = pd.DataFrame([], index=list(index)+["Not bet"])
pred = np.concatenate((pred, np.ones(1)), axis=0)
df["odds"] = odds # オッズ
df["pred"] = pred # 馬券的中確率
df["fraction"] = opts["x"] # 最適化によって得られた投資配分
df["bet"] = np.round(opts["x"] * budget / 100) * 100 # 購入馬券の金額
df["return"] = df["bet"] * odds # 払い戻し金額
return opts["success"], df
上の最適化コードを実行すると以下のような結果が得られます。
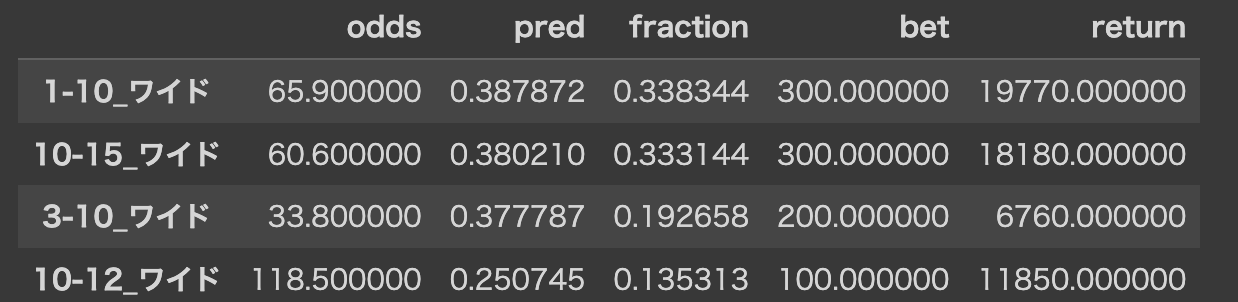
結果から以下のように馬券を購入します。
- 1-10のワイド馬券を300円
- 10-15のワイド馬券を300円
- 3-10のワイド馬券を200円
- 10-12のワイド馬券を100円
実験
購入対象馬券を複勝、ワイドの2つにして、実験を行います。
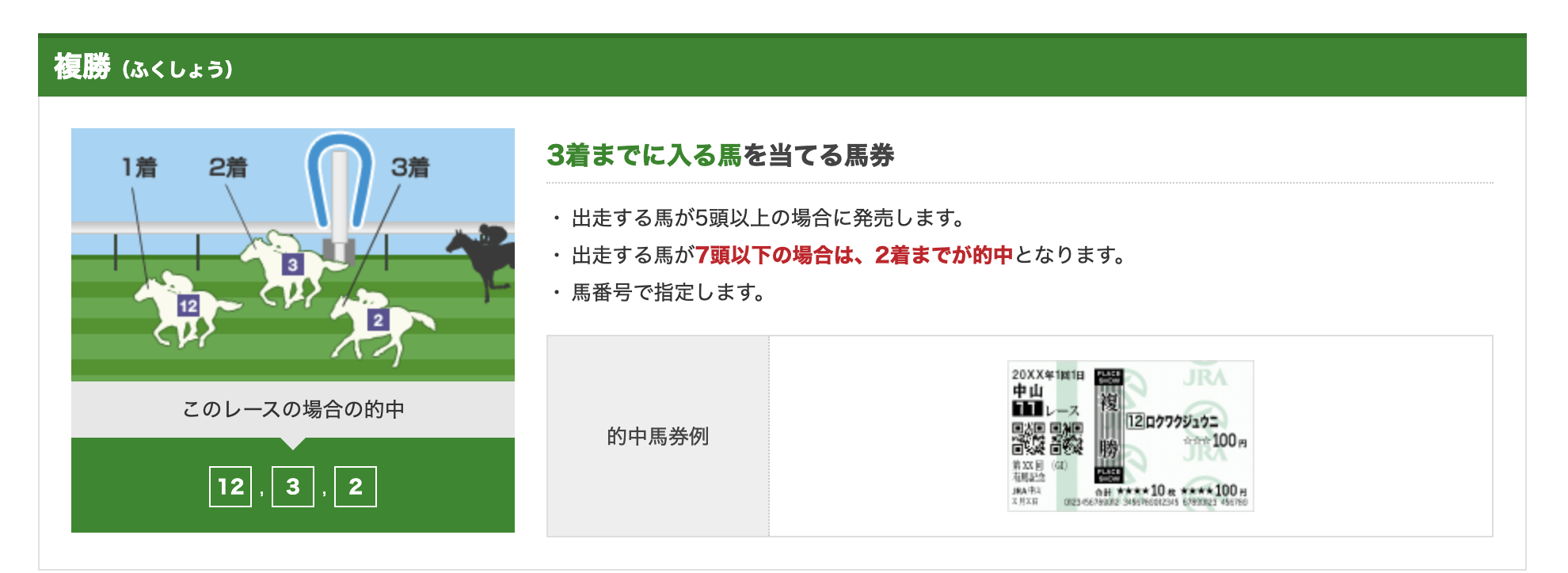
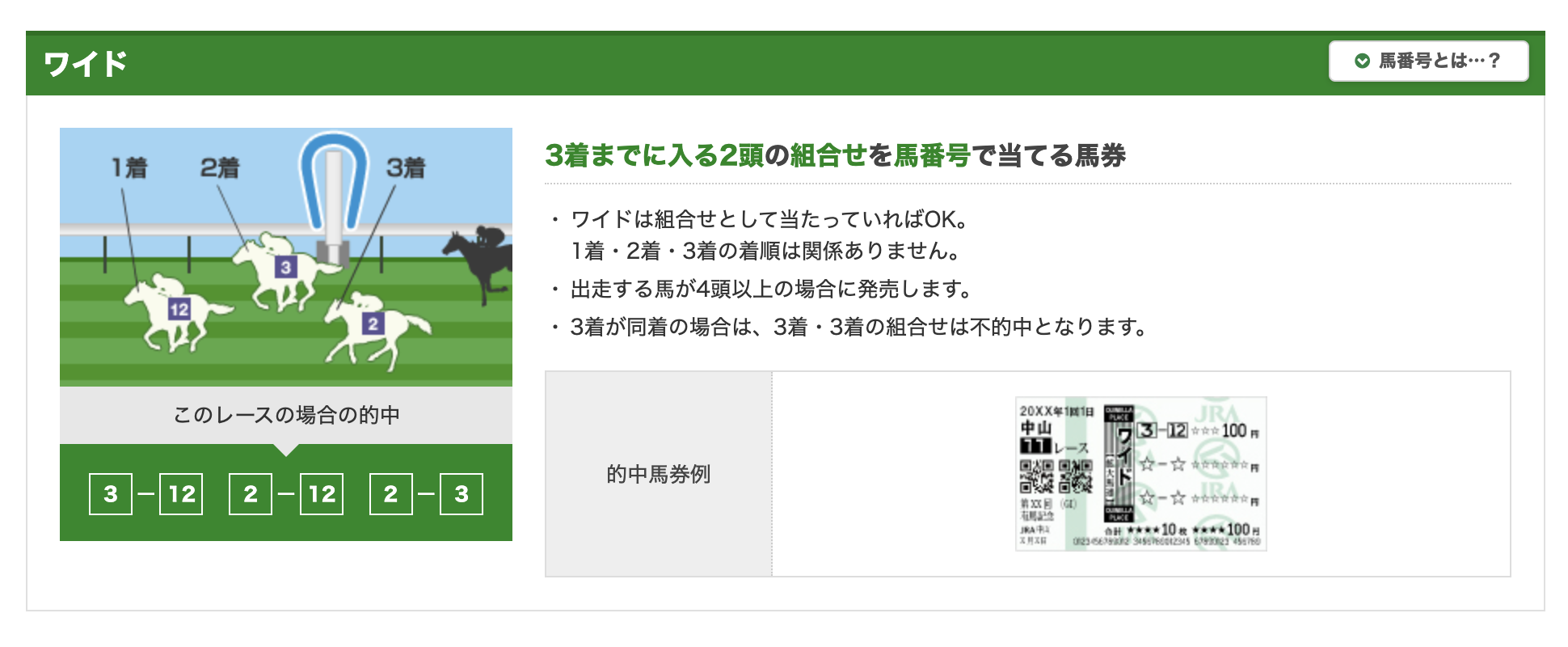
(画像はJRA公式サイトより引用)
予測モデルは該当馬が3着に入る確率を予測します。
複勝馬券の的中確率には予測確率をそのまま使い、ワイド馬券の的中確率は該当馬同志の予測確率の掛け合わせとします。(12番の予測確率が0.3, 3番の予測確率が0.4だった場合、ワイド3-12の予測確率は0.12)
データ
モデル学習データ
JRA-VAN Data-Labからデータを取得します。
データの分割は以下の通りです。
| 期間 | 用途 | |
|---|---|---|
| 学習 | 2015年1月~2022年9月 | モデル学習 |
| 開発 | 2022年6月 ~ 2022年8月 | early stopping |
| テスト | 2022年9月 ~ 2022年11月 | モデル性能の評価 |
オッズデータ
オッズデータはnetkeibaさんのレース情報からスクレイピングして取得しています。
robots.txt(見当たりませんが)、FAQを確認して、サイトに負荷がかからないようtime.sleep(5)を入れ、スクレイピングするページごとに5秒の待ち時間を入れています。
予測モデル
予測モデルはDNNで作成します。
モデルで使用する特徴量には大体2000弱を使用しています。
最適化
上記で説明したコードを使用します。
各レースごとの投資予算は1000円とします。
評価
予測モデルは予測したいレースに出走する馬情報を入力として、「その馬が3着以内に入る確率」を出力します。
テストデータセットにおいて、レースごとに最も確率が高い馬1頭、上位3頭、閾値0.5を超える馬全頭の馬券に対する的中率と回収率は以下の通りです。
的中率は$\frac{予測した馬券が的中した数}{予測馬券数}$で計算し、回収率は$\frac{的中馬券の払い戻し額}{予測した馬券の購入額}$とします。
| 的中率 | 回収率 | |
|---|---|---|
| 上位1頭 | 0.4987 | 0.8486 |
| 上位3頭 | 0.4064 | 0.7808 |
| 閾値(0.5)以上全頭 | 0.4324 | 0.8537 |
単純に複勝を買うだけでは回収率が100%以上になっていません。
実際に賭けてみた
12月17日、12月18日に開催された中央競馬(中山、中京、阪神)で開催された芝コース、計nレースを対象に実験しました。
12月17日 総賭け金額4,600円 総回収金額9,690円
阪神11R ワイド5-6 的中!
12月18日 総賭け金額5,300円 総回収金額9,230円
中京7R ワイド4-12 的中!
的中馬券は2つでしたが、比較的荒れたレースを的中させることができたので十分回収できています。
運がよかっただけかも
改善点
最適化結果
最終的な馬券最適化結果は「〇〇に200円, 〇〇に400円」といった形にしています。実際の最適化結果である総和が1の比率に予算額にかけて、100円以上になった馬券のみを表示する形にしています。そのため本来の最適化結果と購入する馬券にズレが存在しています。
解決方法として、整数計画問題として実装する。制約条件で100円以上賭けない最適化結果は出ないようにするなどを設定することが考えられます。
短期・長期投資計画
今回の実験では1レース単位で予算を設定し、最適化を行なっています。
しかし、1日の全レースの中で見込みのあるレースがある場合には、そこに多くの予算を割り当てる方が良さそうです。どのレースに対して予算を割り当てるかを考えることが可能です。
ひいては、1年間に競馬に使える予算が決まっている場合に「予算があまり残っていないから今日は小さく賭けよう」「予算が潤沢にあるから強気に賭けよう」といった長期的な投資計画を決めることができます。
ケリー基準など有名なものもあるので、なんらかの形で実装は可能ですね。
モデル精度
本記事では特に注目していませんが、予測モデルの精度が直接最適化結果に影響するため、改善するメリットは大きいです。
アーキテクチャについては、今回DNNで作りましたが、LightGBM等の決定木系の方が容易かつ精度がよくなるかもしれません。
まとめ
本記事では、予測モデルの出力である馬券的中確率を基に購入するべき馬券を数理最適化で計算する手法の紹介と実装を行いました。
(以下論文を参考にしています。Optimal sports betting strategies in practice: an experimental review)
検証として不十分ではありますが、作成した予測モデルで2日間実際に最適化結果に従って馬券を購入して、収支プラスになりました。
有馬記念の買い目
アドベントカレンダー2022最終日である12月25日は言わずもがな有馬記念の開催日です。
最後に、予測モデルと最適化によって得られた有馬記念の購入馬券を紹介して、締めとさせていただきます。
(12月25日11時00分時点)
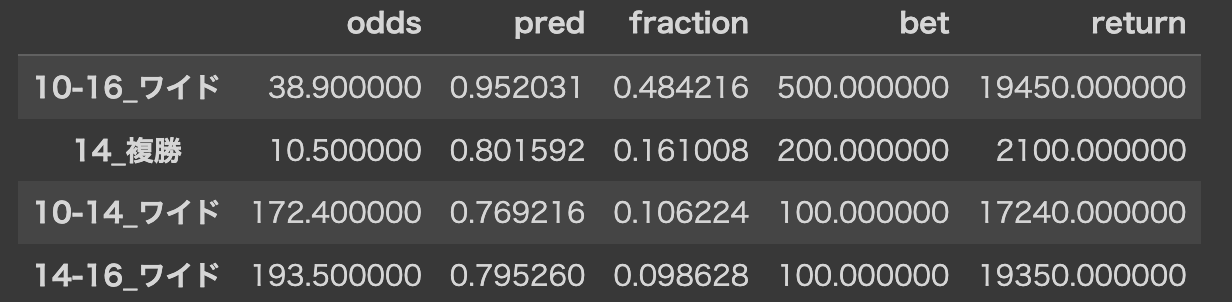
10番(7番人気)、14番(15番人気)、16番(8番人気)と穴狙いすぎですね。
当たったら来年のアドベントカレンダーは1人で25日分書きます。
12月26日追記
結果外れました。
高配当オッズの馬券(複勝で10倍以上、ワイドで100倍以上)は当たるとおいしいですが、そもそもワイドの万馬券は滅多にでないようです。(2010年以降の中央・芝レースのうち3%未満。かつそのレースで的中させる必要がある。)
オッズが高すぎる馬券は最適化対象にしないのが良いかもしれません。もしくは高配当が出るレースを予測して、そこに絞って賭けていくという手もありますね。