Problem
文字列S1とS2の最長共通部分を求めよ. 最長共通部分とは,
S1とS2の要素から順番を保ったまま任意の数の文字を選択した場合に
同一となる文字列のうち, 最長のものを指す.
たとえば, "1224533324" と "69283746" の最長共通部分は "234"である.
Solution
これも有名なDPの問題の1つです. 個人的にはめちゃくちゃ難しいと思います….
Longest Common Substringと似ていますが, 必ずしも要素同士は隣り合っている必要がないという点が異なります.
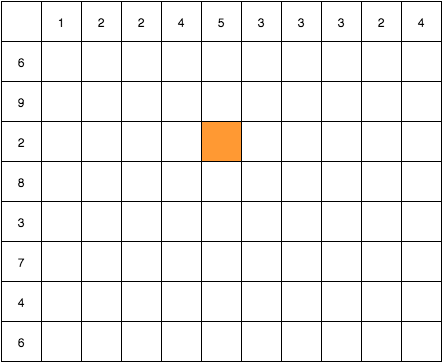
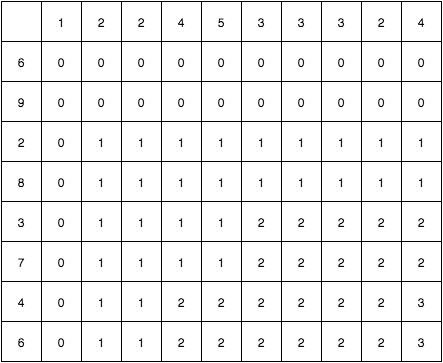
問題の例について考えてみます. 与えられた2つの文字列を縦と横に置いて, 下の図のようなテーブルを考えます.
例えばオレンジ色のセル Table[4][2] は S1.subString(0, 5) = "12245" と S2.subString(0, 3) = "692"の最長共通部分の長さを格納することになります. この問題を解くということは, この表のすべての値を埋めることと同一です.
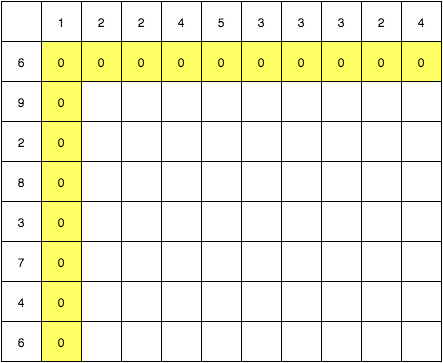
0行目, 0列目から考えます. 例えば0行目, これは "1224533324" は "6" を含むか? "6" を見つけるまでは "0" を, もし見つけたら以降は "1" を埋めよ という問題になります. 残念ながら我々のケースでは "6" は見つからないので, 値はすべて"0"になります. 列についても同様です.
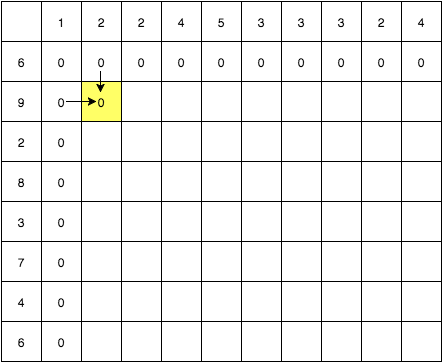
続いて Table[1][1] を見てみます. この場合, S1[1] != S2[1] ですので, その前段の状態, すなわち Table[0][1], Table[1][0], Table[0][0] から最長のLCSをそのまま引き継ぐことになります. ただし Table[0][1] >= Table[0][0], Table[1][0] >= Table[0][0] が成り立つので ( S1[1] == S2[0] もしくは S1[0] == S2[1] の場合, Table[0][1] もしくは Table[1][0] は Table[0][0] + 1 となるため), Table[0][0] を無視して上か左のセルをチェックし, 大きい方を取れば良さそうです.
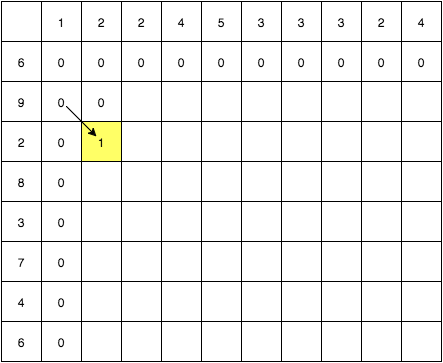
次は Table[1][2] で, S1[1] == S2[2] となっています! したがってLCSの長さを1伸ばすことができます. ここで私たちは同時に, Table[0][1] の状態から斜めにしかこのセルに到達できない ことに気づきます. Table[0][2] と Table[1][1] においては, S1[1] あるいは S2[2] (= "2") が既に考慮済のためです.
ここまで見てきたルールを一般化してみましょう.
Table[i][j] =
Table[i-1][j-1] + 1 if S1[i] == S2[j]
else
Max(Table[i][j-1], Table[i-1][j])
これを順次適用することで, 表をすべて埋めることが可能です.
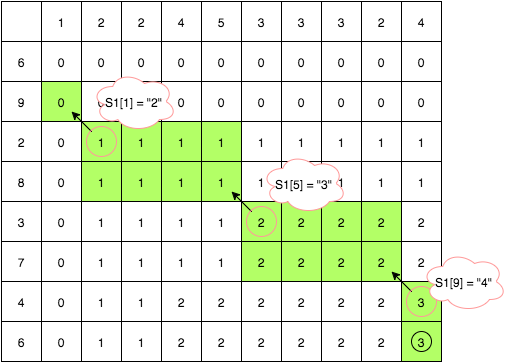
さて, LCSの最長の長さが分かりました. でも, LCSの文字列そのものが欲しい場合はどうしましょう? LCSの長さが伸びるときはつねに斜め下にジャンプする, ということは分かっています. すなわち, LCSの文字列を集めるためには最終的に最長のLCSを得たケースにおいて, 表のどこでジャンプしたのかを調べればよいのです.
コレをチェックするために, テーブルの右下(最終パターン)から始めます. ジャンプしてきた地点においては, S1[i] == S2[j] が満たされているはずです. この点を見つけるまで, セルの上か右に移動しつづけ(LCSの長さを保ちながら), 見つけたら文字を保存して斜め左上に飛んでLCSの長さも1減る, この手順をテーブルの左か上端に到達するまで続ければ良いことがわかります.
上の例では, "4", "3", "2" が保存されますが, これはまさにLCSの逆さまになった形です.
下のコードでは, テーブルの表現として m[i][j] を使っています.
def LCS(s1, s2):
l1, l2 = len(s1), len(s2)
if l1 == 0 or l2 == 0: return ''
# memorization of m[l1][l2]
m = []
for x in range(l1):
m.append([0]*(l2))
# Fill 0th row
isSameFound = False
for i in range(l1):
if isSameFound or s1[i] == s2[0]:
m[i][0] = 1
isSameFound = True
# Fill 0th column
isSameFound = False
for j in range(l2):
if isSameFound or s2[j] == s1[0]:
m[0][j] = 1
isSameFound = True
max_len = 0
# m[i][j] stores the maximum length of subsequence of s1[:i+1], s2[:j+1]
for i in range(0, l1-1):
for j in range(0, l2-1):
if s1[i+1] == s2[j+1]:
m[i+1][j+1] = m[i][j] + 1
max_len = max(m[i][j], max_len)
else:
m[i+1][j+1] = max(m[i][j+1], m[i+1][j])
#If you want to know just the length of the lcs, return maxLen.
#Here we'll try to print the lcs.
lcs_str = ''
i, j = l1-1, l2-1
while i >= 0 and j >= 0:
if s1[i] == s2[j]:
lcs_str += s1[i] #or s2[j-1]
i -= 1
j -= 1
else:
if m[i-1][j] > m[i][j-1]:
i -= 1
else:
j -= 1
return lcs_str[::-1]
計算量は O(MN) + O(M+N) = O(MN),
空間量は O(MN). (m[M][N]を保持するため).
# M, N はそれぞれの文字列の要素数.
Jave版コードはこちら:
import java.lang.Math;
public class Solution {
public static String LCS(String s1, String s2) {
if (s1.isEmpty() || s2.isEmpty()) {
return "";
}
int l1 = s1.length();
int l2 = s2.length();
// memorization
int[][] m = new int[l1][l2];
int maxLen = 0;
// fill the 0th row
boolean isFound = false;
for (int i = 0; i < l1; i++) {
if (isFound || s1.charAt(i) == s2.charAt(0)) {
m[i][0] = 1;
isFound = true;
} else {
m[i][0] = 0;
}
}
// fill the 0th column
isFound = false;
for (int j = 0; j < l2; j++) {
if (isFound || s2.charAt(j) == s1.charAt(0)) {
m[0][j] = 1;
isFound = true;
} else {
m[0][j] = 0;
}
}
// m[i][j] stores the maximum length of subsequence until s1.subString(0, i+1), s2.subString(0, j+1)
for (int i = 1; i < l1; i++) {
for (int j = 1; j < l2; j++) {
if (s1.charAt(i) == s2.charAt(j)) {
m[i][j] = m[i-1][j-1] + 1;
maxLen = Math.max(m[i][j], maxLen);
} else {
m[i][j] = Math.max(m[i-1][j], m[i][j-1]);
}
}
}
// If you want to know just the length of the lcs, return maxLen.
// Here we'll try to print the lcs.
StringBuilder sb = new StringBuilder();
int i = l1 - 1, j = l2 - 1;
while (i > 0 && j > 0) {
if (s1.charAt(i) != s2.charAt(j)) {
if (m[i-1][j] > m[i][j-1]) i--;
else j--;
} else {
sb.append(s1.charAt(i)); // or s2.charAt(j-1)
i--; j--;
}
}
return sb.reverse().toString();
}
}