AtCoder初心者、ARCに参加してみたけど一問も解けなくて萎えたので復習します

はじめに

2022/4/9に開催された「大和証券プログラミングコンテスト2022 Spring(AtCoder Regular Contest 138)」に参加したのですが、A問題のTLEを解決できず終わったので、復習します。
問題リンク：https://atcoder.jp/contests/arc138/tasks/arc138_a

問題

長さ N の整数列 $A=(A_1, A_2, \cdot\cdot\cdot, A_N)$ があります．以降この問題では，$A$ の先頭 $K$ 項の和をスコアと呼ぶことにします． また，入力で与えられた $A$ のスコアを $s$ と置くことにします．

あなたは，以下の操作を好きな回数繰り返すことができます．

• $A$ のある隣接する2要素を選び，それらの値を入れ替える．

あなたの目標は，スコアを $s+1$ 以上にすることです． 目標が達成可能であるかどうか判定し，また可能であるなら必要な最小の操作回数を求めてください．

＜制約＞

• $2≤N≤4×10^5$
• $1≤K≤N−1$
• $1≤A_i≤10^9$
• 入力される値はすべて整数

解法

値の入れ替えの最小操作回数について、インデックス $i$ と $j$ の2つの数を入れ替える場合、以下のように操作して $j-i$ 回で入れ替えが可能。

• インデックス $i$ の数をインデックス $K-1$ まで後ろに持ってくる
• インデックス $j$ の数をインデックス $K$ まで前に持ってくる
• インデックス $K-1$ と $K$ を交換

交換の対象とする数は、 $A_i<A_j$ となりかつ $j-i$ が最小のもの。
これを探すのに、標準入力で受け取った配列の順序を変えずにそのまま総当たりで条件に合うものを探してリストに $j-i$ をappend、最後に出来上がったリストの中で最小の値を出力していた…。これは非常に効率が悪い。

元のindexとsortを使って効率よく答えを求める。

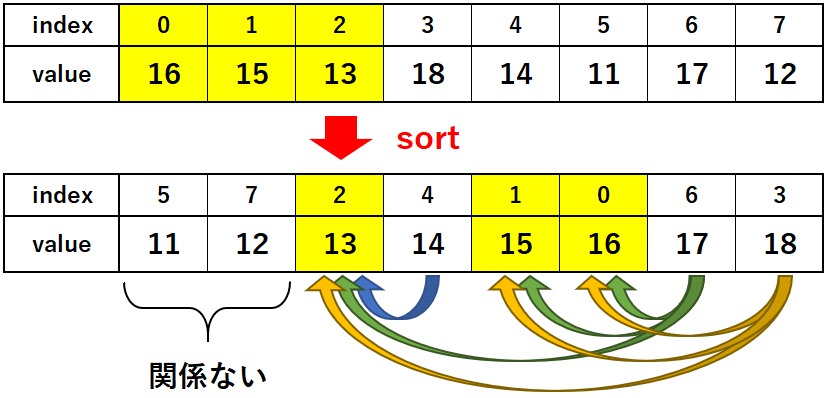
図で黄色になっているのが先頭 $K$ 項。
上が標準入力で得られたリストのイメージで、sortすると下のようになる。
ソート後に頭からインデックスを見ていき、先頭二つの先頭 $K$ 項に入っていない数は、絶対に $A_i<A_j$ が満たせないので関係ない。
先頭 $K$ 項の数に対して、それ以降の（sort済みなのでより大きい）先頭 $K$ 項に入っていない数とでindexの差 $j-i$ を計算して、それが最小のものを保存すればいい。
なお、図には各先頭 $K$ 項に入っていない数から先頭 $K$ 項の数まで矢印を付したが、実際は全てのインデックスとの差分を取る必要はなく、インデックスが最大（リストの後ろ側）の数のインデックスのみ保存しておけば十分。
注意しなければならないのは、sortの際にただ単純にsortすると、値が同じでインデックスが異なる場合に、インデックスが大きいものが後ろに来てしまう。
これだと後ろにあるにも関わらず $A_i<A_j$ が満たせなくなる。
また、これをif文で回避することも可能だが、そうするとインデックスの最大値として更新した値と同じ値を持つ先頭 $K$ 項に入っていない数が順序決めに加わらなくなり、考慮漏れが発生する。
従って、valueに対して昇順、indexに対して降順にsortすればよい。
以下のようなコードを書けばOK。

n, k = map(int, input().split())
a = list(map(int, input().split()))
a_idx = [[a[i], i] for i in range(n)]
a_idx = sorted(a_idx, key=lambda x: (x[0], -x[1]))

max_k_idx = -1
ans = 10**6

for val, j in a_idx:
    if j < k:
        max_k_idx = max(max_k_idx, j)
    elif max_k_idx != -1:
        ans = min(ans, j - max_k_idx)

if ans == 10**6:
    print(-1)
else:
    print(ans)