JavaScriptとRust(WebAssembly)でグラフの深さ優先探索のベンチマーク

はじめに

前々からRust + WebAssemblyでネットワーク可視化のライブラリを作っていましたが、使い勝手を良くするためのFFI（Foreign Function Interface）、つまりJavaScript側とRust側のどちらでデータを持つのか、そして他方にどのようなインタフェースを提供するのかの設計には悩まされていました。そこで今回は、グラフ処理の基本の一つである深さ優先探索（DFS）でベンチマークをとり、性能面での比較を行いました。私のアプリケーションでは、RustとJavaScript双方でアルゴリズムを書くこともあるため、グラフデータ構造の隣接リストとDFSのそれぞれをJavaScriptとRustの両方で実装し、4通りの組み合わせを比較します。

実装

それぞれの実装の一部を記載します。全体のソースコードは GitHubのリポジトリ をご覧ください。

隣接リストのJavaScriptによる実装

今回のベンチマークに必要最低限の以下の4つのメソッドを実装します。

• addNode(u) ：頂点 $u$ を追加する
• addEdge(u, v) ：辺 $(u, v)$ を追加する
• neighbors(u) ：頂点 $u$ の隣接頂点を返す
• nodeCount() ：グラフの頂点数を返す

実プロジェクトで使用していたJavaScript実装の隣接リストから必要な機能のみを取り出し以下のような実装にしました。

export class GraphJs {
  constructor() {
    this.nodes = new Map();
  }

  addNode(u, obj = {}) {
    this.nodes.set(u, {
      neighbors: new Map(),
      data: obj,
    });
    return this;
  }

  addEdge(u, v, obj = {}) {
    this.nodes.get(u).neighbors.set(v, obj);
    this.nodes.get(v).neighbors.set(u, obj);
    return this;
  }

  neighbors(u) {
    return this.nodes.get(u).neighbors.keys();
  }

  nodeCount() {
    return this.nodes.size;
  }
}

頂点や辺の削除を考慮しなければ配列の配列などにしてしまえばより高速化ができますが、ある程度実用的なデータ構造を前提として Map を使用しました。

隣接リストのRustによる実装

隣接リスト自体はpetgraphを使用します。JavaScript側からアクセスするために以下のようにWebAssemblyのインタフェースを実装します。JavaScript側へ提供する関数はJavaScriptによる実装と同様です。

#[wasm_bindgen]
impl GraphRust {
    #[wasm_bindgen(constructor)]
    pub fn new() -> GraphRust {
        GraphRust {
            graph: GraphType::with_capacity(0, 0),
        }
    }

    #[wasm_bindgen(js_name = addNode)]
    pub fn add_node(&mut self, value: JsValue) -> usize {
        let value = if value.is_null() || value.is_undefined() {
            Object::new().into()
        } else {
            value
        };
        self.graph.add_node(value.into()).index()
    }

    #[wasm_bindgen(js_name = addEdge)]
    pub fn add_edge(&mut self, u: usize, v: usize, value: JsValue) -> usize {
        let value = if value.is_null() || value.is_undefined() {
            Object::new().into()
        } else {
            value
        };
        let u = node_index(u);
        let v = node_index(v);
        self.graph.add_edge(u, v, value.into()).index()
    }

    #[wasm_bindgen(js_name = neighbors)]
    pub fn neighbors(&self, a: usize) -> Array {
        self.graph
            .neighbors(node_index(a))
            .map(|u| JsValue::from_f64(u.index() as f64))
            .collect::<Array>()
    }

    #[wasm_bindgen(js_name = nodeCount)]
    pub fn node_count(&self) -> usize {
        self.graph.node_count()
    }
}

なお、petgraphの neighbors は隣接ノードのイテレータを返しますが、WebAssemblyのレイヤーでは Array を返すようにしました。これは、JavaScriptのイテレータに変換した場合、頻繁にRust側からJavaScript側への変換が生じるため、Array に変換して返した方が処理速度が速かったためです。また、Rust側からイテレータを返した場合に、手動でイテレータのメモリ解放が必要で使い勝手も良くありませんでした。

DFSのJavaScriptによる実装

隣接リストは、RustとJavaScriptの両方で同じインタフェースを持つため、JavaScriptによるDFSの実装は一つにまとめて以下のように実装しました。

const rec = (graph, u, depth) => {
  for (const v of graph.neighbors(u)) {
    if (depth[v] === 0) {
      depth[v] = depth[u] + 1;
      rec(graph, v, depth);
    }
  }
};

const dfsJs = (graph) => {
  const depth = new Array(graph.nodeCount());
  depth.fill(0);
  depth[0] = 1;
  return rec(graph, 0, depth);
};

DFSのRustによる実装

RustによるDFSの実装は、入力のグラフがJavaScriptの場合とRustの場合でそれぞれ別の関数を用意します。

以下はJavaScript実装の隣接リスト用です。

fn dfs_rec(graph: &GraphJs, u: usize, depth: &mut Vec<usize>) {
    for v in graph
        .neighbors(u)
        .into_iter()
        .map(|v| v.ok().unwrap().as_f64().unwrap() as usize)
    {
        if depth[v] == 0 {
            depth[v] = depth[u] + 1;
            dfs_rec(graph, v, depth);
        }
    }
}

fn dfs(graph: &GraphJs) -> Vec<usize> {
    let mut depth = vec![0; graph.node_count()];
    depth.insert(0, 1);
    dfs_rec(graph, 0, &mut depth);
    depth
}

#[wasm_bindgen(js_name = dfsRustWithJs)]
pub fn dfs_js(graph: GraphJs) -> Array {
    dfs(&graph)
        .into_iter()
        .map(|u| JsValue::from_f64(u as f64))
        .collect::<Array>()
}

続いて、以下はRust実装の隣接リスト用です。

fn dfs_rec(graph: &GraphType, u: NodeIndex, depth: &mut Vec<usize>) {
    for v in graph.neighbors(u) {
        if depth[v.index()] == 0 {
            depth[v.index()] = depth[u.index()] + 1;
            dfs_rec(graph, v, depth);
        }
    }
}

fn dfs(graph: &GraphType) -> Vec<usize> {
    let mut depth = vec![0; graph.node_count()];
    depth[0] = 1;
    dfs_rec(graph, node_index(0), &mut depth);
    depth
}

#[wasm_bindgen(js_name = dfsRustWithRust)]
pub fn dfs_rust(graph: &GraphRust) -> Array {
    dfs(&graph.graph)
        .into_iter()
        .map(|u| JsValue::from_f64(u as f64))
        .collect::<Array>()
}

traitで両方の実装をまとめられるとカッコ良いので試したのですが、neighbors のシグネチャを fn neighbors<'a>(&'a self, u: NodeIndex) -> Box<dyn Iterator<Item = NodeIndex> + 'a>; としたところ、Box<dyn trait> の影響か、JavaScriptとRust両方で処理速度が落ちたので断念しました。

グラフ生成

$n = |V|$ 頂点のグラフ $G = (V, E)$ の各頂点ペアについて、$p$ の確率で辺を生成するランダムグラフを使用します。いわゆるErdős–Rényiモデルです。

なお、DFSの計算量のオーダーは $O(|E|)$ で、辺数 $|E|$ の期待値は $p n(n - 1) / 2$ となります。

実行結果

$n$ を 100 から 1000 まで 100 毎に、$p=0.1$ として 10 個のグラフを生成してベンチマークを取りました。実行時間の測定には benchmark.js を使用しています。以下のページで実際に実行することができます。

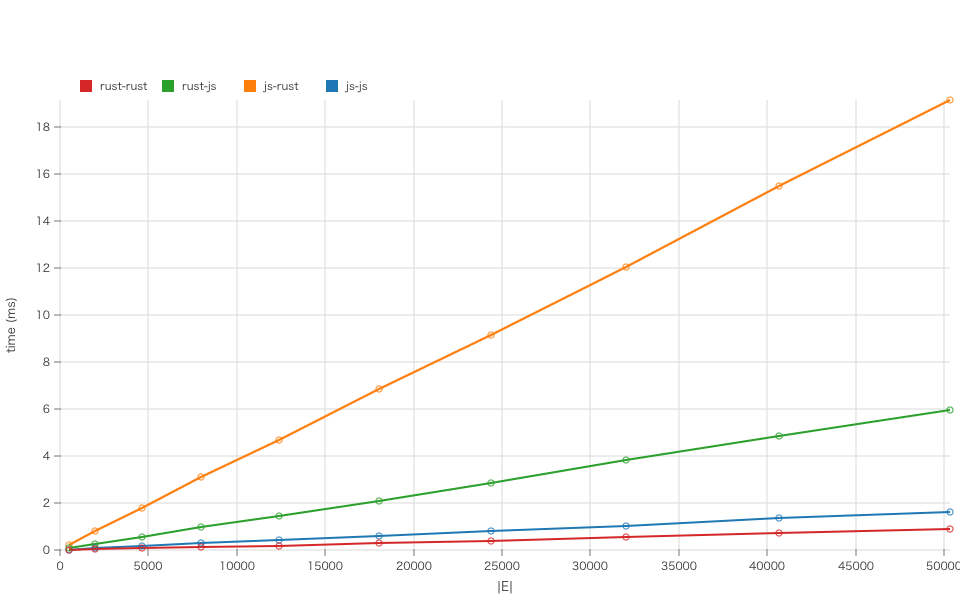
横軸に辺数 $|E|$、縦軸にbenchmark.jsによって得られた平均実行時間をとったグラフを次に表します。

実装の種類を 言語1-言語2 の形式で表していて、言語1が隣接リストの実装、言語2がDFSの実装を表しています。両方ともRustによる実装が最も速く、そこから2倍程度の時間で両方ともJavaScriptによる実装が続きます。JavaScriptとRustを組み合わせた場合は、最速の場合からおよそ一桁遅くなる結果となりました。

実行環境は以下の通りです。

Mac mini (2018)
プロセッサ：3.2 GHz 6コア Intel Core i7
メモリ：16GB 2667 MHz DDR4

Google Chrome：バージョン: 84.0.4147.89

まとめ

今回のベンチマークの結果、調査した範囲ではグラフのサイズによらず、Rustによる隣接リストの実装の方がトータルの計算時間は短くなることが確認できました。私のユースケースでは、安心してRustによる実装で進められそうです。

その他、当たり前のことですが、言語の境界をまたいだデータのやり取りが高コストであることが確認できました。頻繁に境界をまたぐ場合は、WebAssemblyの恩恵が十分に得られない可能性があるので、データの受け渡し方法を検討する必要があります。

今回の単純なベンチマークでは、RustとJavaScriptの性能差は2倍程度となりました。単純なプログラムだとJavaScriptは 気持ち悪いぐらい 非常に速いことがあります。しかし、数千行にわたる複雑なアルゴリズムを、性能を保ちながらJavaScriptで実装するのは少々難しくなります。また、将来的にWebAssemblyでSIMDやThreadsの恩恵を受けられるようになることを考えると、今回の結果で十分なアドバンテージを示すことができたと思います。