グラフ描画
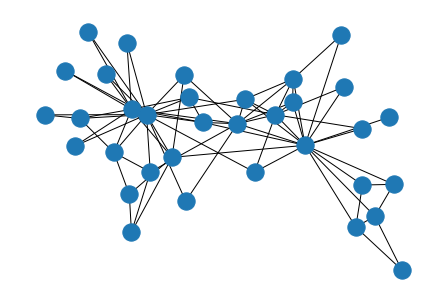
人間生きていると誰しもネットワークの可視化をしたくなるものです。ネットワーク可視化の代表的な表現方法は、2次元空間中にノードを配置しノードを結ぶエッジを線で表す ノードリンク図 です。3次元空間を扱う場合もありますが、本稿では2次元に限定することにします。下図は、Karate Clubグラフ1として知られるネットワークのノードリンク図です。
ネットワークの構造は グラフ として表されます。いわゆるグラフ理論で扱うグラフのことです。グラフ $G$ は、ノードの集合 $V$ とエッジの集合 $E$ によって $G = (V, E)$ と表されます。また、ノード数とエッジ数をそれぞれ $n = |V|, m = |E|$ としておきます。なお、本稿では単純連結無向グラフのみを扱うことにします。
さて、グラフ自身はノードの座標の情報を持たないため、ノードリンク図を描くためには、グラフを入力としてノードの座標を求める必要があります。そのような方法の総称が グラフ描画(Graph Drawing) です。ノードの座標を以下のように表すことにします。
X = \left(
\begin{array}{c}
X_1\\
X_2 \\
\vdots \\
X_n
\end{array}
\right)
ここで、 $X_i = (x_i, y_i)$ はノード $i$ の座標です。グラフ描画とはつまり、$X = f(G)$ のように $X$ を出力する $f$ を上手く設計することとなります。
グラフ描画のアルゴリズムは数多く提案されていて、Handbook of Graph Drawing and Visualization2等の分厚い教科書で網羅的に解説されています。上記の図はFruchterman-Reingoldのアルゴリズム3として知られる古典的なグラフ描画アルゴリズムを使用しています。本稿では、それらの数多くあるアルゴリズムの中でも、Stress Majorizationによるグラフ描画について紹介します。Stress Majorizationは、物理的なアナロジーに基づいたグラフ描画アルゴリズムの中でも、エネルギー関数の最小化を明示的に行うため、視認性の高いレイアウトを生成しやすいという特徴があります。詳細は元論文4もご参照ください。
グラフ描画のストレスモデル
「良いノードの配置」とは何か考えてみましょう。様々な考え方があると思いますが、一つの考え方として、ノード $i$ とノード $j$ について、あらかじめ決められた理想的な距離 $d_{ij}$ と実際に配置された2点間のユークリッド距離 $||X_i - X_j||$ の差は小さい方が良いと考えることができるでしょう。グラフに含まれる全てのノードのペアについて、この2乗誤差の重み付き和を ストレス として以下のように表します。
\text{stress(X)} = \sum_{i<j} w_{ij}(||X_i - X_j|| - d_{ij})^2
ここで、$w_{ij}$ はノード $i$ とノード$j$ のペアの重みです。$d_{ij}$ は、直接エッジで結ばれていないノードペアについても決めておく必要がありますが、グラフの最短経路アルゴリズムによって得られた最短経路長を採用することが考えられます。このストレス関数を最小化するようなノードの配置 $X$ は「良いノードの配置」であると考えても良いでしょう。
さて、このストレス関数は別の見方をすることもできます。ノード $i$ とノード $j$ を自然長が $d_{ij}$ 、バネ定数が $\frac{w_{ij}}{2}$ のバネで結ばれているとします。全てのノードペアをこのようなバネで結んだときに、弾性エネルギーはストレスと一致します。すなわち、ストレスを最小化することは、バネで結ばれたノード群のエネルギーを最小化することを意味しています。
Stress Majorization
さて、とにかくストレス関数を最小化したい気持ちは伝わったと思いますが、ストレス関数は非凸関数であり簡単に最小化をすることができません。ストレス関数を最小化するために 優関数法(Majorization Technique) を使用します。優関数法については、既にQiitaにわかりやすい解説があったので紹介しておきます。
大雑把に言うと、ある性質を満たした最小化しやすい補助関数を導入すれば、補助関数を最小化することで元関数の目的関数値を小さくすることができるのが優関数法です。
実は、グラフのストレス関数は上記の記事で紹介されている多次元尺度構成法(MDS; Multi Dimensional Scaling)のストレスと同一なので導出も同様になります。一応グラフを使って補助関数を導入します。
ストレス関数を展開し、以下のように変形します。
\begin{aligned}
\text{stress}(X) &= \sum_{i<j} w_{ij} ||X_i - X_j||^2 - 2 \sum_{i<j} w_{ij} d_{ij} ||X_i - X_j|| + \sum_{i<j} w_{ij} d_{ij}^2 \\
&= \text{tr}(X^T L^w X) - 2 \delta_{ij} ||X_i - X_j|| + \sum_{i<j} w_{ij} d_{ij}^2
\end{aligned}
ここで、$\delta_{ij} = w_{ij} d_{ij}$ です。また、 $L^w$ は重み付きラプラシアンで次のように定義されます。
\begin{aligned}
L^w &= [L_{ij}^w] \\
L_{ij}^w &= \begin{cases}
-w_{ij} & i \neq j \\
\sum_{k \neq i} w_{ik} & i = j
\end{cases}
\end{aligned}
重み付きラプラシアンは半正定値行列となることが知られています。
変形したストレス関数の第3項は定数、第1項は凸二次関数ですが、第2項は最適化をする上で性質が良くありません。
そこで、次の行列 $L^Z$ を導入します。
\begin{aligned}
L^Z &= [L_{ij}^Z] \\
L_{ij}^Z &= \begin{cases}
-\delta_{ij} \text{inv}(||Z_i - Z_j||) & i \neq j \\
-\sum_{k \neq i} L_{ik}^Z & i = j
\end{cases} \\
\text{inv}(x) &= \begin{cases}
\frac{1}{x} & x \neq 0 \\
0 & x = 0
\end{cases}
\end{aligned}
さらに、ストレス関数の第2項を置き換えた関数 $F^Z(X)$ を次のように定義します。
F^Z(X) = \text{tr}(X^T L^w X) - 2 \text{tr}(X^T L^Z Z) + \sum_{i<j} w_{ij} d_{ij}^2
$F^Z(X)$ は次の2つの性質を満たします。
\begin{aligned}
\text{stress}(X) &\leq F^Z(X) \\
\text{stress}(Z) &= F^Z(Z)
\end{aligned}
これらは優関数法における補助関数の性質であり、$F^Z(X)$ を補助関数として使用することでストレス関数の値を減少させることができます。また、次に示すように $F^Z(X)$ の最小解は比較的容易に求めることができます。
補助関数の最小化
$F^Z(X)$ の最小化を考えます。重み付きラプラシアンは半正定値行列でしたが、キルヒホッフの行列木定理(Kirchhoff's Matrix Tree Theorem)により、(重み付き)ラプラシアンからいくつかのノードに対応する行と列を取り除いた部分行列は正定値になることが知られています。つまり、一つのノードを適当に選び、その座標を $(0, 0)$ に固定すれば、 $F^Z(X)$ は狭義凸関数となります。
よって、$\nabla F^Z(X) = 2 L^w X - 2 L^Z Z = 0$ となる $X$ が最小解となります。すなわち、以下の連立方程式を解くことで $F^Z(X)$ の最小解が得られます。
L^w X = L^Z Z
一つのノードの座標を $(0, 0)$ に固定しているため、それ以外のノードについての係数行列は正定値行列となっています。そのため、共役勾配法等の連立方程式解法を使用すればこの連立方程式を解くことができます。
Stress Majorizationによるグラフ描画
以上で理論的な準備は整いました。Stress Majorizationによるグラフ描画のアルゴリズムを整理すると以下のようになります。
- グラフの最短距離行列 $D = [d_{ij}]$ を求める。
- 初期座標 $Z$ を生成する。
- ストレス関数の減少が十分に小さくなるまで以下を繰り返す。
- $L^w X = L^Z Z$ の解を$Z$に代入する。
- $Z$ を最適ノード配置として出力する。
Pythonによる実装
細かいことは気にせずにPythonで実装してみます。結局のところコアな計算は連立方程式を解くだけになるので、SciPyの共役勾配法を使用しておきます。
from math import sqrt
from random import random
from networkx import floyd_warshall_numpy
from scipy.sparse.linalg import cg
import numpy as np
def inv(x):
if x < 1e-4:
return 0.0
return 1 / x
def stress(X, D):
n = len(X)
s = 0
for i in range(n):
X_i = X[i, :]
for j in range(i):
X_j = X[j, :]
d = np.linalg.norm(X_i - X_j) - D[i, j]
s += d * d
return s
def stress_majorization(graph):
epsilon = 1e-4
n = graph.number_of_nodes()
D = floyd_warshall_numpy(graph)
w = np.zeros((n, n))
delta = np.zeros((n, n))
for i in range(n):
for j in range(i):
w[i, j] = w[j, i] = D[i, j] ** -2
delta[i, j] = delta[j, i] = w[i, j] * D[i, j]
Z = np.random.rand(n, 2)
Z[0] = (0., 0.)
L_w = np.zeros((n, n))
for i in range(n):
for j in range(i):
L_w[i, j] = L_w[j, i] = -w[i, j]
for i in range(n):
L_w[i, i] = -sum(L_w[i, :])
e0 = stress(Z, D)
while True:
L_Z = np.zeros((n, n))
for i in range(n):
Z_i = Z[i, :]
for j in range(i):
Z_j = Z[j, :]
L_Z[i, j] = L_Z[j, i] = -delta[i, j] * inv(np.linalg.norm(Z_i - Z_j))
for i in range(n):
L_Z[i][i] = -sum(L_Z[i, :])
Z[1:, 0] = cg(L_w[1:, 1:], (L_Z @ Z[:, 0])[1:])[0]
Z[1:, 1] = cg(L_w[1:, 1:], (L_Z @ Z[:, 1])[1:])[0]
e = stress(Z, D)
if (e0 - e) / e0 < epsilon:
break
e0 = e
return {u: Z[i] for i, u in enumerate(graph.nodes())}
描画結果
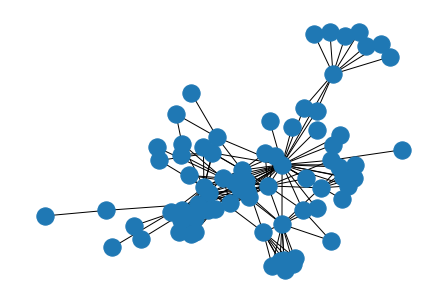
Karate ClubグラフおよびLes Miserablesグラフを用いて、実装したStress MajorizationとNetworkXで実装されているFruchterman-Reingold、Kamada-Kawaiによる描画結果の比較を行います。全てのケースでエッジの長さを100に設定しました。描画結果は次の表のようになりました。
| 描画アルゴリズム | Karate Club | Les Miserables |
|---|---|---|
| Stress Majorization | 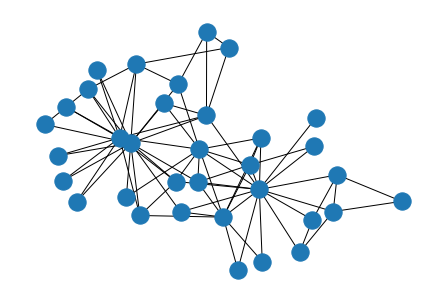 |
 |
| Fruchterman-Reingold | 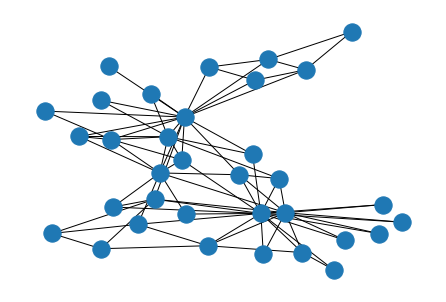 |
 |
| Kamada-Kawai | 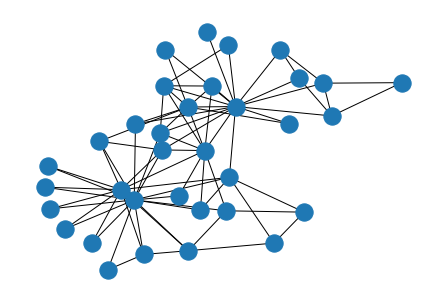 |
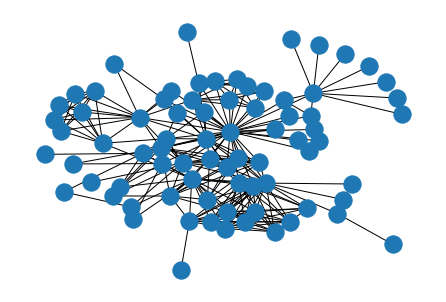 |
まず、Stress Majorizationが問題なくノードの配置に成功していることがわかります。Fruchterman-Reingoldは、明示的なストレス関数の最小化は行わないため、少しゴチャっとした部分が見られます。Kamada-Kawaiは、Stress Majorizationと同様にストレス関数の最小化の行うため、比較的綺麗なレイアウトが生成されます。しかし、最適化の観点では、Stress Majorizationの方がより良い最小解を見つけやすかったり、収束が早いといったメリットがあります。
おわりに
本稿では、グラフ描画アルゴリズムの一種であるStress Majorizationを紹介しました。Stress Majorizationによるグラフ描画は、ライブラリ等で実装されてることが珍しいせいか、グラフ描画の専門家以外にはあまり有名ではないように思います。ですが、個人的には、綺麗な描画結果を生成できることが多く、最近勉強した中で気に入っているアルゴリズムの一つです。
最後に、Stress Majorizationを改良・拡張した研究を3つ紹介しておきます。
制約付きStress Majorization
本稿で扱ったストレスモデルは制約なし凸最適化ですが、これにノードの座標に関する線形制約を加えても凸最適化の枠組みでStress Majorizationを適用することが出来ます。このような、Stress Majorizationを拡張する研究がいくつか報告されています56。また、これらの研究成果は、cola.js というJavaScriptライブラリに実装されており、Web等のプラットフォームでも非常に高いクオリティのレイアウトを生成することができます。
確率勾配法
Stress Majorizationの弱点の一つは計算量です。ストレスモデルでは全てのノードペアの最短経路を求める必要があり、Floyd-Warshallのアルゴリズムで $O(n^3)$、Johnsonのアルゴリズムで $O(n^2 \log n + n m)$ の計算量がかかります。これを改善するために、スパースストレスモデルと確率勾配法を使用した高速なアルゴリズムが提案されています6。
双曲面上でのグラフ描画
双曲面上でグラフ描画を行った結果をポアンカレディスクを用いて投影することで、魚眼レンズのように着目箇所を強調表示するような視覚効果が得られます7。双曲面上でのグラフ描画にストレスモデルと確率勾配法を適用した研究が報告されています8。
-
Zachary, W. W. (1977). An information flow model for conflict and fission in small groups. Journal of anthropological research, 33(4), 452-473. ↩
-
Tamassia, R. (Ed.). (2013). Handbook of graph drawing and visualization. CRC press. ↩
-
Fruchterman, T. M., & Reingold, E. M. (1991). Graph drawing by force‐directed placement. Software: Practice and experience, 21(11), 1129-1164. ↩
-
Gansner, E. R., Koren, Y., & North, S. (2004, September). Graph drawing by stress majorization. In International Symposium on Graph Drawing (pp. 239-250). Springer, Berlin, Heidelberg. ↩
-
Dwyer, T., & Koren, Y. (2005, October). Dig-CoLa: directed graph layout through constrained energy minimization. In IEEE Symposium on Information Visualization, 2005. INFOVIS 2005. (pp. 65-72). IEEE. ↩
-
Zheng, J. X., Pawar, S., & Goodman, D. F. (2018). Graph drawing by stochastic gradient descent. IEEE transactions on visualization and computer graphics, 25(9), 2738-2748. ↩ ↩2
-
Kobourov, S. G., & Wampler, K. (2005). Non-Eeuclidean spring embedders. IEEE Transactions on Visualization and Computer Graphics, 11(6), 757-767. ↩
-
Miller, J., Kobourov, S., & Huroyan, V. (2022, April). Browser-based Hyperbolic Visualization of Graphs. In 2022 IEEE 15th Pacific Visualization Symposium (PacificVis) (pp. 71-80). IEEE. ↩