QAOAを用いた車両塗装最適化
はじめに
QAOA(Quantum approximate optimization algorithm:量子近似最適化アルゴリズム)とはゲート方式の量子コンピュータを用いた組合せ最適化計算を行う量子アルゴリズムで、様々な最適化問題へ適用する研究が行われています。
今回は、下記の論文を参考にQAOAを用いた車両塗装の最適化問題に挑戦してみます。
まずはQAOAの概要を確認し、論文の問題設定にそって実装を行います。
その後、パラメータやビット数を変えて比較実験を行い、正答率や処理時間の変化を確認します。
概要
組合せ最適化問題とは、あるコスト関数を最小化するような変数の組み合わせを求めることです。
今回は最適化問題として定式化されているバイナリー・ペイントショップ問題に量子コンピュータのアルゴリズムであるQAOAを適用してみます。
QAOAはノイズのある量子デバイス(NISQ)上で組合せ最適化問題を解決するため手法の一つとして広く研究されています。
QAOA(量子近似最適化アルゴリズム)とは
QAOAの計算フロー
まずは、今回用いるQAOAの計算フローを確認していきます。
まずは古典最適化問題のコスト関数$C(x)$をコストハミルトニアンを用いて量子化します。
$$
H_c |x \rangle = C(x)|z \rangle
$$
このコストハミルトニアン$H_c$の最小固有値を見つけることとコスト関数の最適解を見つけることは同等の意味を持ちます。
コストハミルトニアンの固有値を見つけるために、下記の手順を実行します。
コストハミルトニアンから得られるコスト演算子
$$
U_c (\gamma)= e^{-i\gamma H_c}
$$
とqubitの初期状態を決めるミキサーハミルトニアン$H_M$から得られるミキサー演算子$U_M$を定義します。
$$
H_M = \sum_j^n \sigma_j^x \
U_M (\beta)= e^{-i\beta H_M}
$$
ここでの$\gamma$と$\beta$は古典最適化アルゴリズムによって最適化されるパラメータで、$\sigma_j^x$は$j$番目の量子ビットに作用するパウリ$x$演算子です。
初期状態はミキサーハミルトニアン$H_M$の基底状態$|s \rangle$とし、下記のようにこのコスト演算子$U_c$とミキサー演算子$H_M$を交互に繰り返し適用します。
$$
|\gamma,\beta \rangle = U_M (\beta_p) U_c (\gamma_p)...U_M (\beta_1) U_c (\gamma_1) |s \rangle
$$

(図は参考論文の4.2節の図2より引用)
ここで、$p$は繰り返し回数(QAOAの階層)を表します。
このとき、パラメータ$\gamma$、$\beta$を古典最適化アルゴリズムを用いてコストハミルトニアンの期待値を最小にするように最適化します。
$$
\min \langle \gamma,\beta |H_c|\gamma,\beta \rangle
$$
アルゴリズムの考え方イメージ
上記手順で行っていることのイメージとしてはQuantum Adiabatic Algorithm(QAA・量子断熱計算)という考え方がベースになっています。
量子断熱計算とは簡単にいうと、全体のハミルトニアンを自明な基底状態を持つミキサーハミルトニアン$H_M$から求めたい結果を基底状態とするコストハミルトニアン$H_c$へ、少しずつ断熱的に変化させます。このとき初期状態をミキサーハミルトニアンの基底状態とすることで、コストハミルトニアン$H_c$の基底状態へ少しずつ変化していくため、欲しい解を得られるという考え方です。
このハミルトニアンの変化を式で表すと下記になります。
$$
H(t)= (1-\frac{t}{T})H_M + \frac{t}{T}H_c
$$
時間$t=0$のときはミキサーハミルトニアン$H_M$が支配的で、$t=T$になるにつれコストハミルトニアン$H_c$が支配的になることがわかります。
このハミルトニアンを持つシュレディンガー方程式
$$
-i\frac{\partial}{\partial t}|\psi \rangle = H(t)|\psi \rangle
$$
の解$U(t)$をトロッター展開して時刻tを離散化します。
このときの$\Delta t$が、QAOAの計算フロー内でミキサーハミルトニアンの基底状態$|s \rangle$に作用させた$U_M (\beta_p) U_c (\gamma_p)...U_M (\beta_1) U_c (\gamma_1)$の$\beta$と$\gamma$と対応します。
QAOAの場合、階層$p$を無限にすることが、終状態の時刻$T$を無限にすることに相当します。つまり、階層$p$の無限の極限をとることで最適解に収束すると考えられます。
しかし、階層$p$を増加させると回路が深くなってしまうため、実際には$p$は1や2で計算することが多いです。
コスト関数の導出
ここからは、コスト関数を導出していきます。
今回考える問題は自動車製造の塗装工程で発生するコストを少なくする車両塗装順番を求める、という最適化問題になります。
そこで、今回は決定変数である車両塗装順番を下記のように表すとします。
x_{it} = \left\{
\begin{array}{ll}
1 & 車両v_iがt番目に塗装される\\
0 & \mathrm{otherwise}\\
\end{array}
\right.
つまり、車両$n$台を考える場合、決定変数は$n \times n$行列となり、3台の車両の塗装シーケンスを表す場合は下記の$3 \times 3$行列になります。
\boldsymbol{x}=
\begin{bmatrix}
0 & 1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1
\end{bmatrix}
この行列は車両$v_2$、車両$v_1$、車両$v_3$の順番で塗装されることを表しています。
次に、2種類のコストを考えます。
1つ目のコストは、色変更コストです。
例えば、次に塗装する車両の色が前の車両の色と異なる場合、塗装ロボットは前の色を洗浄し、次の車両の色に変更する必要があります。この洗浄作業により、材料と塗装時間の損失関数が発生します。これが色変更コストであり、一回の色変更のコストを$r_{cc}$と表します。
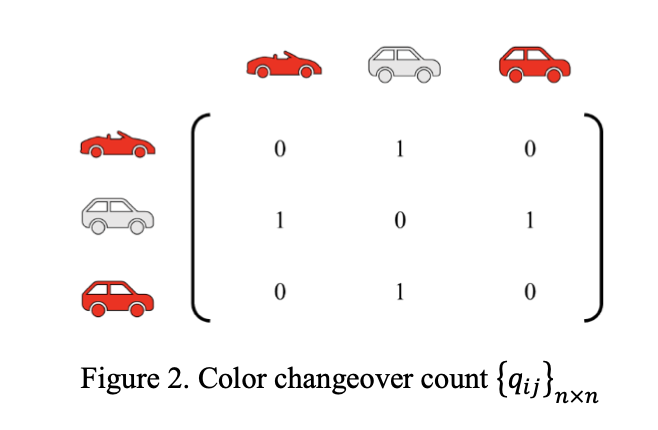
車両$v_j$(車両の色:$c_j$)の次に車両$v_i$(車両の色:$c_i$)が塗装される場合、色変更回数$q_{ij}$は以下となります。
q_{ij} = \begin{cases}
1 & c_i \neq c_j \\
0 & \mathrm{otherwise}
\end{cases}
つまり、この場合の色変更コストは$q_{ij}r_{cc}$となります。
2つ目のコストは、修理コストです。
これは品質不良の発生確率$p_{ij}$とその修理費$r_{pr}$の積(修理費の期待値)$p_{ij}r_{pr}$で表します。
品質不良の発生確率$p_{ij}$は塗装する車両の順番に依存し、車両$v_{j}$の次に車両$v_{i}$を塗装した時に車両$v_{i}$に品質不良が発生する確率を表します。また、これは古典の機械学習モデルで出力された結果を使用します。
上記の決定変数、2つのコストを踏まえるとコスト関数は下記のようになります。
\begin{align}
C(x) = \sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}(q_{ij}r_{cc} + p_{ij}r_{pr})\sum\limits_{t=2}^{n}x_{j(t-1)}x_{it}
\\
\mathrm{s.t} \sum\limits_{i=1}^{n} x_{it} = 1, \forall t=1,2,\ldots,n \\
\sum\limits_{t=1}^{n} x_{it} = 1, \forall i=1,2,\ldots,n
\end{align}
1個目の制約式は、$x$の各横列はひとつだけが1となることを表しており、これは各車両は一度のみ塗装されるという条件です。
2個目の制約式は、$x$の各縦列はひとつだけが1になることを表しており、これは各時刻でひとつの車のみを塗装するという条件です。
これら2つの制約式の代わりに、制約条件を満たさない場合に値が高くなるような項をペナルティ項としてコスト関数に加えることで、制約のない最適化問題に変換します。
c(x) = \sum\limits_{i=1,j=1}^{n}(q_{ij}r_{cc} + p_{ij}r_{pr})
\sum\limits_{t=1}^{n-1}x_{jt}x_{i(t+1)}
+\alpha\sum\limits_{i=1}^{n}\bigg(\sum\limits_{t=1}^{n}x_{it}-1\bigg)^2
+\alpha\sum\limits_{t=1}^{n}\bigg(\sum\limits_{i=1}^{n}x_{it}-1\bigg)^2
(上式は参考論文の4.1節(8)式ですが、第1項二つ目の$\sum$の範囲はおそらく誤植であるため、変更しています。)
第二項、第三項が制約式の代わりに追加したペナルティ項であり、$\alpha$を十分大きな値にすることで制約を満たさない場合のコストが大きくなることがわかります。
実装
上記の考え方に基づき、実装していきます。
パラメータ設定
今回は参考論文の設定に従い、3つの車両の塗装順序を求めていきます。つまり9量子ビットの計算になります。
車両$v_i$はそれぞれ$v_1 = {\mathrm{red}, \mathrm{style A}}$、$v_2 = {\mathrm{white}, \mathrm{style B}}$、$v_3 = {\mathrm{red}, \mathrm{style B}}$です。
色変更の回数を示す行列$q_{ij}$を下の図に示します。
次に、品質不良の発生確率$p_{ij}$を示します。これは、古典機械学習モデルで事前に出力された結果を用います。
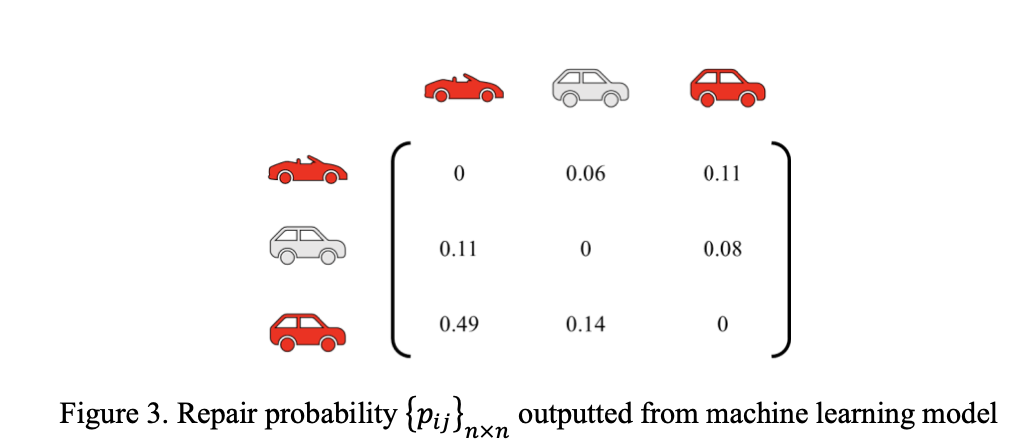
(図は参考論文の5.1節の図3より引用)
また、一回の色変更コスト$r_{cc}= 20$で、修理コストは$r_{pr}=100$とします。
QAOAの階層は$p=3$とします。
コード
今回利用するライブラリのバージョンは以下の通りです。
Python 3.10.3
numpy 1.23.5
sympy 1.12
qiskit 0.23.2
tytan 0.0.19
まずは必要なライブラリをインポートします
from qiskit_optimization import QuadraticProgram
from typing import Tuple, Dict
from tytan import symbols, Compile
import sympy as sym
import numpy as np
from qiskit import Aer
from qiskit.algorithms import QAOA
from qiskit.opflow import I, X, Y
from qiskit_optimization.algorithms import MinimumEigenOptimizer
次に、上記で求めたコスト関数を定義し、そのコスト関数の計数をQiskitのQuadraticProgram()モジュールに渡します。
#最適化する9個の0と1の変数
x = sym.symbols("q0:9")
#色変更行列q_ij
q_ij=np.array([[0,1,0],[1,0,1],[0,1,0]])
#品質不良発生確率p_ij
p=np.array([[0,0.06,0.11],[0.11,0,0.08],[0.49,0.14,0]])
#色変更コスト
r_cc = 20
#修理コスト
r_pr = 100
#コスト関数
HA=0
for i in range(3):#i
for j in range(3):#j
cost=q_ij[i][j]*r_cc +p_ij[i][j]*r_pr
for t in range(0,2):#t
HA+=cost*x[j+3*t]*x[i+3*(t+1)]
#制約式
#同じ車両は1回のみ塗装
HB=(x[0]+x[1]+x[2]-1)**2+(x[3]+x[4]+x[5]-1)**2+(x[6]+x[7]+x[8]-1)**2
#各時刻で塗装する車両はひとつ
HC=(x[0]+x[3]+x[6]-1)**2+(x[1]+x[4]+x[7]-1)**2+(x[2]+x[5]+x[8]-1)**2
#結合 α=200
alpha = 200
C=HA+ alpha * HB + alpha * HC
# Taytan SDKのCompile関数を使用 重複している係数をまとめる
Q, offset = Compile(C).get_qubo()
# 線形項と2次項に分ける関数
LinearInfo = Dict[str, int | float]
QuadraticInfo = Dict[Tuple[str, str], int | float]
def make_linear_and_quadratic(Q: dict) -> Tuple[LinearInfo, QuadraticInfo]:
linear: LinearInfo = {}
quadratic: QuadraticInfo = {}
for key, coeff in Q.items():
key0, key1 = key
if key0 == key1:
linear[key0] = coeff
else:
quadratic[(key0, key1)] = coeff
return linear, quadratic
linear, quadratic = make_linear_and_quadratic(Q)
print(linear, quadratic)
#QiskitのQuadraticProgram()モジュールにコスト関数の係数を渡す
qubo = QuadraticProgram()
qubo.binary_var('q0')
qubo.binary_var('q1')
qubo.binary_var('q2')
qubo.binary_var('q3')
qubo.binary_var('q4')
qubo.binary_var('q5')
qubo.binary_var('q6')
qubo.binary_var('q7')
qubo.binary_var('q8')
qubo.minimize(linear=linear, quadratic=quadratic)
次にQAOAの初期状態とそれに対応するミキサーハミルトニアンを作成します。
参考論文に合わせ、初期状態は各qubitにアダマールゲートをかけた状態($|+ \rangle $)とし、ミキサーハミルトニアンはこの初期状態を基底状態とするものとします。
from qiskit import QuantumCircuit
#初期状態
initial_state_circuit = QuantumCircuit(9)
initial_state_circuit.h(0)
initial_state_circuit.h(1)
initial_state_circuit.h(2)
initial_state_circuit.h(3)
initial_state_circuit.h(4)
initial_state_circuit.h(5)
initial_state_circuit.h(6)
initial_state_circuit.h(7)
initial_state_circuit.h(8)
#ミキサーハミルトニアン
mixer = (X^I^I^I^I^I^I^I^I) \
+ (I^X^I^I^I^I^I^I^I) \
+ (I^I^X^I^I^I^I^I^I) \
+ (I^I^I^X^I^I^I^I^I) \
+ (I^I^I^I^X^I^I^I^I) \
+ (I^I^I^I^I^X^I^I^I) \
+ (I^I^I^I^I^I^X^I^I) \
+ (I^I^I^I^I^I^I^X^I) \
+ (I^I^I^I^I^I^I^I^X)
最後にQAOAで最適な塗装順序を求めます。
backend = Aer.get_backend('aer_simulator')
backend.set_options(device='CPU', cuStateVec_enable=True)
step = 3
qaoa_mes = QAOA(quantum_instance=backend, reps=step, initial_state=initial_state_circuit, mixer=mixer)
qaoa = MinimumEigenOptimizer(qaoa_mes)
qaoa_result = qaoa.solve(qubo)
print(qaoa_result)
QAOAで計算した結果、下記のように最適な塗装順序が出力されました。
\boldsymbol{x}=\left[
\begin{matrix}
0 & 0 & 1 \\
1 & 0 & 0 \\
0 & 1 & 0
\end{matrix}
\right]
これは塗装順序が車両$v_3 = {\mathrm{red}, \mathrm{style B}}$、$v_1 = {\mathrm{red}, \mathrm{style A}}$、$v_2 = {\mathrm{white}, \mathrm{style B}}$であり、色変更回数は最小の1回になることを表しています。
修理コストを100と低い値にしているため、色変更コストの影響が相対的に高くなっていると考えられます。
比較実験
ここからは参考論文の内容から少し外れて、ビット数やQAOAの階層などパラメータを一部変更したものとの簡単な比較実験をしてみたいと思います。
ビット数を増やすにあたり、色変更行列$q_{ij}$、品質不良発生確率行列$p_{ij}$は適宜定義します。
4台の塗装最適化の準備
まずは台数を3台から4台に増やすための準備をします。
ビット数は9bitから16bit($4 \times 4$行列)になります。
4台用の色変更行列$q_{ij}$、品質不良発生確率行列$p_{ij}$は参考論文で示されていないため、それぞれ下記を設定しました。
q_{ij}=\left[
\begin{matrix}
0 & 1 & 0 & 1 \\
1 & 0 & 1 & 0 \\
0 & 1 & 0 & 1 \\
1 & 0 & 1 & 0
\end{matrix}
\right]
p_{ij}=\left[
\begin{matrix}
0 & 0.06 & 0.11 & 0.20 \\
0.11 & 0 & 0.08 & 0.30 \\
0.49 & 0.14 & 0 & 0.40 \\
0.30 & 0.05 & 0.08 & 0
\end{matrix}
\right]
この場合の最適解は以下になります。
\boldsymbol{x}
=\left[
\begin{matrix}
0 & 0 & 1 & 0 \\
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1
\end{matrix}
\right]
結果と考察
上記の設定でペナルティ項の係数$\alpha$と階層$p$を変えながら、またシミュレーテッドアニーリング(SA)でも実行した結果を下記にまとめます。
試行回数はQAOAでそれぞれ10回、シミュレーテッドアニーリングでは100回です。
3台の塗装最適化

4台の塗装最適化

階層$p$を増加させると、計算時間も増加しますが、正答率はほとんど変化しませんでした。階層$p$を増加させることで回路が深くなり最適化するパラメータ数が増えるので、計算時間が増加するのは直感通りですが、正答率の変化がないことはQAOAの考え方からすると意外です。ただ、もっと階層を深くすることで正答率があがる可能性はありますが、計算時間が伸びるため今回は実行できませんでした。
一方で、ペナルティ項の係数$\alpha$増加させても計算時間はほとんど変化せず、正答率は上昇する傾向が見られました。これは$\alpha$がペナルティ項以外の項の大きさと比較して大きくなる領域($\alpha \geq 100$)で最適解が求まりやすくなっていると考えられます。
ただし、古典最適化と同じく、問題によってはペナルティ項の影響を受けやすくなり、正答率が下がる現象が起こる可能性があります。
ビット数を増やすと計算時間は増加し、正答率も下がり、ほとんど最適解を算出することができませんでした。今回利用したシミュレータでは3台の塗装最適化が限度のようです。
また、シミュレーテッドアニーリングの結果と比較すると、正答率ではQAOAの方が勝るものの、処理時間はアニーリングの方がはるかに早い結果となりました。
1回でも最適解が求まれば良いということを考えると、現状は試行回数を稼ぎやすいアニーリングの方に分があると言えそうです。
まとめ
今回はバイナリー・ペイントショップ問題を例にQAOAを実装してみました。少ないビット数(9bit程度)では計算可能で、そこそこの確率で最適解が得られることがわかりました。
より多くのビット数(車両台数)を最適化すると、処理時間が増大し正答率も下がります。そのため、現時点では実用段階には至っていませんが、将来量子コンピュータが商用利用規模まで発展すれば利用できる可能性はあると思います。