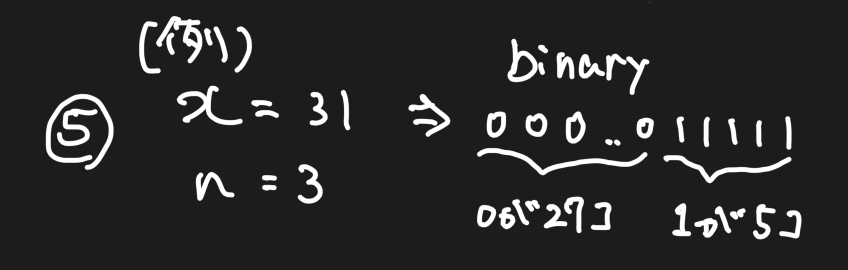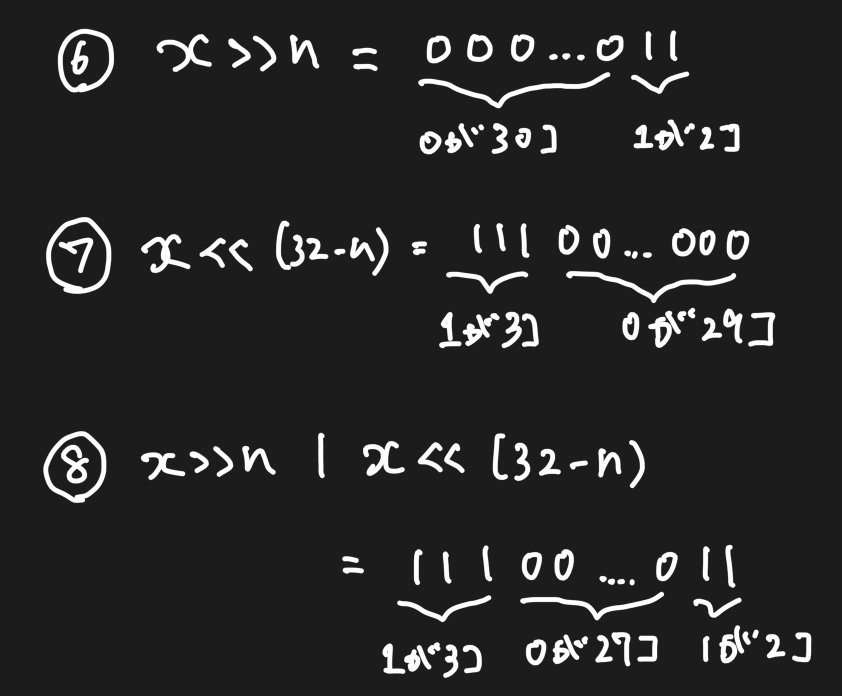はじめに
ハッシュ関数はデータの整合性確認や暗号学的な用途でよく使用されます。この記事では、ハッシュ関数の中でもよく使われるSHA-256を自分で実装しつつ、なぜ元の値を復元できない(不可逆性)の性質を持つのか確認します。
結論はハッシュ関数の不可逆性は、情報の喪失により実現されています。
また、今回sha256を実装したRustのコードは以下です。
https://github.com/akira-19/algorithms_rust/tree/main/sha-256
SHA-256のフロー
不可逆性がわかるところまでのSHA-256のフローは以下のようになっています。
"msg"という文字列をハッシュ化します。
-
まずmsgという文字列を文字コードに置き換えます。(16進数表記)
-
次に、メッセージを64バイトの1つのまとまりにします。この際に、元のメッセージのすぐ後ろに0x80を追加し、64バイトの最後の8バイトには元のメッセージのバイナリでの長さを追加します。つまり、msgは3バイトなので、バイナリでは長さは24(bit)になります。16進数表記では18となります。追加した0x80とメッセージの長さの間は全て0でパディングします。
-
64バイトのまとまりを、4バイトずつ分けます(表記が16進数から10進数に変わっているので注意して下さい)。つまり、最初の6d 73 67 80がまとまって、6d736780になります(こちら10進数に直すと1836279680となります)。
-
Wという値を計算するのですが、この中で不可逆な処理をしています。以下Rustでのサンプルコードです(処理は一部分のみ)。
fn calc_w(msg: [u32; 16]) -> [u32; 64] { let mut w = vec![0; 64]; for i in 0..16 { w[i] = msg[i]; } for i in 16..64 { w[i] = lower_sigma_1(w[i - 2]) .wrapping_add(w[i - 7]) .wrapping_add(lower_sigma_0(w[i - 15])) .wrapping_add(w[i - 16]); } w } fn lower_sigma_1(x: u32) -> u32 { rotr(x, 17) ^ rotr(x, 19) ^ shr(x, 10) } fn rotr(x: u32, n: u32) -> u32 { (x >> n) | (x << (32 - n)) } fn shr(x: u32, n: u32) -> u32 { x >> n }calc_wの中でlower_sigma_1という関数を呼んでおり、さらにその中でrotrという関数を呼んでいます。こちらを図解します。 -
ここでは例としてx=31, n=3とします。31は2進数で11111です。xもnも符号なしの32bit整数ですので、データ上は000..000011111(0が27個)となります。
-
x >> nはxをnだけ右にビットシフトする処理ですので、左側に000を追加して、後ろの111を削除します。 -
同様に
x << (32-n)はxを右に32-3=29個だけシフトさせますので、最初の3つは111となり、あとは0になります。 -
最後に6と7のビット論理和をとるので、111000...0011のようになります。
ポイントは6,7,8の処理です。例えば6の処理でx=30、n=3とします。すると、000..0011110を右に3つシフトするので、000..011となり、x=31の時と同じ返り値になります。
今回の例では3ビット分の情報が失われているので、2進数で000~111(10進数で0~7)までの情報が失われているため、この処理だけ見てもxが24~31の間のどの数値か分からなくなります。
上記のrotrだけだと、右側にシフトして喪失した分は左側のシフトで残っているので情報喪失していないですね。(右にシフトして消えた分のビットが左側に戻ってくる)
情報が喪失するのは、shrでした。6の処理だけを行なっているので、右側にシフトして消えた分は元には戻せません。
また、lower_sigma_1の中で、rotr(x, 17) ^ rotr(x, 19)という処理をしていますが、これも情報を喪失していますね。すごい簡略化した例で説明するとこの処理は、10000を右に1ビットずらしたものと2ビットずらしたものの論理積をとっているようなもので、01000 ^ 00100 = 00000となります。これだと、元の値が00000だとしても同じ結果になります。
このような処理を繰り返すことで、元の値を復元できなくさせます。
まとめ
ハッシュ値は元の値を取得するのが難しいのではなく、原理的にはアルゴリズムで元の値を得るのは不可能ということがわかりました。もちろん、sha256の出力は32バイト(256ビット)なので、32バイト以内の入力であれば無限の計算能力があるコンピュータがあれば、2^256通りの入力を確かめることで、元の値を得ることはできます。(入力と出力が32バイト内で全て1対1対応する前提です)