この記事はTSG Advent Calendar 2017/IS18er Advent Calendarの12日目の記事として書かれました。
(ちょっとタイトルが大げさすぎる?)
はじめに
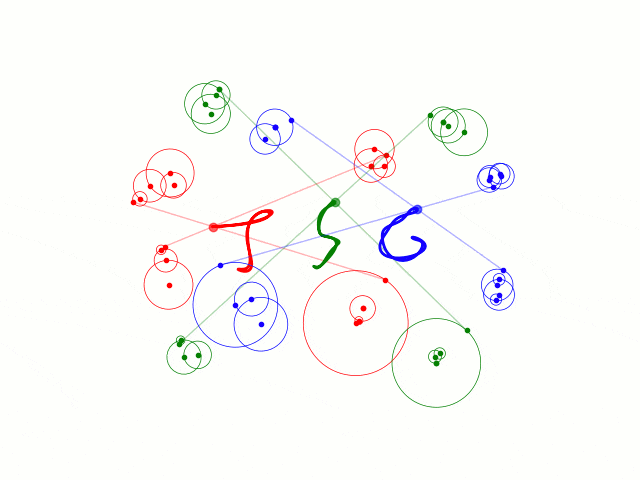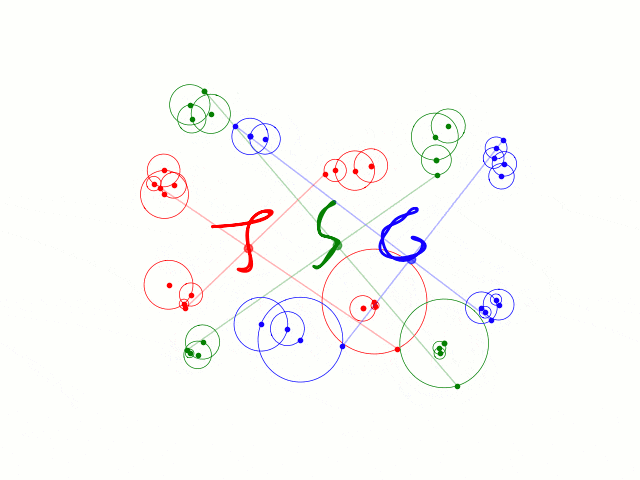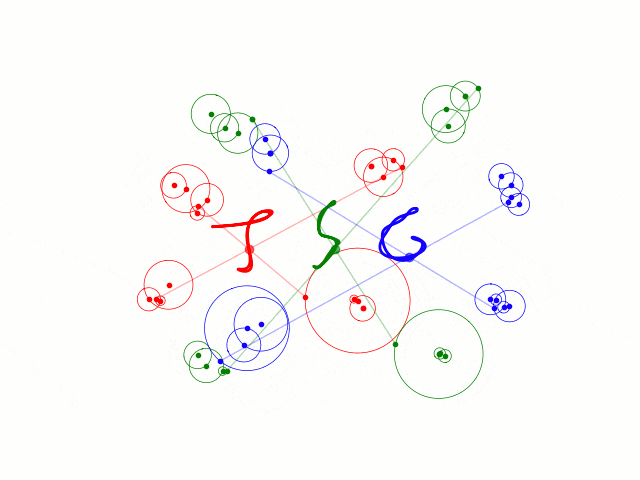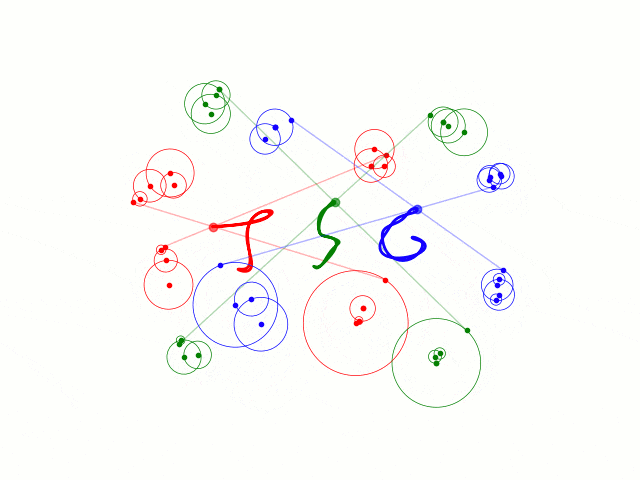
こんなものをchainerで作りました。(アニメーションはmatplotlib)
以下で出てくるコードをまとめたものはここにあります。
ソースファイル
経緯
この間ネットサーフィンをしていたらこんなものを見つけました。
最適化数学で新年の挨拶(ニコニコ動画)
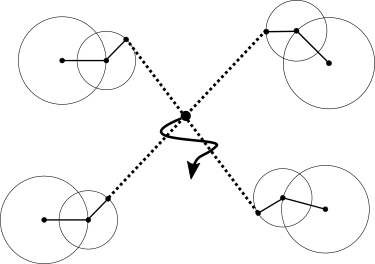
見てみると定点の周りを別の点が回り、さらにその点の周りを別の点が回り…を繰り返し、それらの点を結んでいろいろな図形を作っているようです。この動画では数字の2, 0, 9を描いていました。
これを僕も作りたい!と思ったので、この方のブログへ行き解説を読んでみました。(http://kogarashi.net/pitchblende/archives/12)
これによると、
- 4つの点(恒星)とその周りを公転する4点(惑星)、更にそれを回る4点(衛星)を元に作られている。
- 4衛星を2組にわけ2本の直線を作り、その交点に文字を描かせる。
肝心の軌道ですが、目的の軌道を(大体)等間隔の点に分け、各時刻にその点にできるだけ近づくように係数を最適化しているようです。
そこで今回はchainerの最適化を使ってこれを作ってみました。
数式の作成
[12/12追記] Gistのコードと違っていたのでちょっと書き直しました。前のやつはもしかしたら動かない?
惑星や衛星の軌道は公転運動$e^{i\pi(\omega t + \phi)}$の線形結合で表すことができ、その係数は各円の半径を表します。これをpythonで書くと次のようになります。(円を少し増やし、衛星の衛星なども実装しています)
class unit(chainer.Chain): # 恒星、惑星、衛星などをまとめたもの
def __init__(self, x, y): # 諸事情あって恒星の初期座標は与える(後述)
super().__init__()
self.dim = 3 # 動点の数
with self.init_scope():
self.omega = chainer.Parameter(
np.random.rand(self.dim, 1).astype(np.float32) * 10 - 5)
self.phi = chainer.Parameter(
np.random.rand(self.dim).astype(np.float32))
self.link = chainer.Parameter(
np.random.rand(1, self.dim).astype(np.float32) * .5) # 各円の半径
self.xbias = chainer.Parameter(
initializer=np.array(x, np.float32), shape=(1,)) # 恒星のx座標になる
self.ybias = chainer.Parameter(
initializer=np.array(y, np.float32), shape=(1,))
def __call__(self, time): # timeの値域は[0, 1)を想定
_omega = F.floor(self.omega) # omegaは整数にしたい
phase = F.linear(np.c_[time], F.floor(_omega), self.phi) * np.pi * 2
x = F.cos(phase) # x,y座標は別々に計算
y = F.sin(phase)
x = F.linear(x, self.link, self.xbias)
y = F.linear(y, self.link, self.ybias)
return x, y
複素数でエレガントにやりたかったのですが、望みのドキュメントが見つからなかったので諦めました(もしかして実装されてないのかな?)__call__(self, time)内でomegaを整数にしているのは、一周期(ここではtime=1)経過したとき全ての点がもとに戻ってほしいからです。
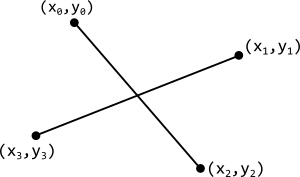
\begin{eqnarray*}
&&\left\{\begin{array}{c}
y = \frac{y_2-y_0}{x_2-x_0}(x-x_0)+y_0 \\
y = \frac{y_3-y_1}{x_3-x_1}(x-x_1)+y_1
\end{array}\right. \\
\Leftrightarrow&& \left\{\begin{array}{c}
(y_0-y_2)x+(x_2-x_0)y = y_0x_2-x_0y_2 \\
(y_1-y_3)x+(x_3-x_1)y = y_1x_3 - x_1y_3
\end{array}\right. \\
\Leftrightarrow&& \left[\begin{array}{cc}
y_0-y_2&x_2-x_0\\
y_1-y_3&x_3-x_1
\end{array}\right]\left[\begin{array}{c}
x\\
y
\end{array}\right] = \left[\begin{array}{c}
y_0x_2-x_0y_2\\
y_1x_3 - x_1y_3
\end{array}\right] \\
\Leftrightarrow&& \left[\begin{array}{c}
x\\
y
\end{array}\right] = \left[\begin{array}{cc}
y_0-y_2&x_2-x_0\\
y_1-y_3&x_3-x_1
\end{array}\right]^{-1} \left[\begin{array}{c}
y_0x_2-x_0y_2\\
y_1x_3 - x_1y_3
\end{array}\right]
\end{eqnarray*}
(ここら辺外積とか使ってもうちょっとうまくやれませんかね)
ここでは2直線が平行にならないということを前提としているので、学習時に大体の点の位置関係を与えておきます。そのために恒星の初期位置は手で指定します。
これで最終的な点の位置が分かります。
class Model(chainer.Chain):
def __init__(self, offset):
"""offset [[x0, y0], [x1, y1], ...]"""
super().__init__()
self.train = True
with self.init_scope():
self.u0 = unit(*offset[0])
self.u1 = unit(*offset[1])
self.u2 = unit(*offset[2])
self.u3 = unit(*offset[3])
self.u = [self.u0, self.u1, self.u2, self.u3]
def calc(self, time):
"""最終的な点の位置を返す"""
x = []
y = []
for i in range(4):
unit_x, unit_y = self.u[i](time)
x.append(unit_x)
y.append(unit_y)
A = F.reshape(F.concat((y[0]-y[2], x[2]-x[0], y[1]-y[3], x[3]-x[1])), (-1,2,2))
Mat = F.batch_inv(A)
vec = F.reshape(F.concat((y[0]*x[2] - x[0]*y[2], y[1]*x[3]-x[1]*y[3])), (-1,1,2))
return F.matmul(vec, Mat, transb=True)
def __call__(self, time, teacher):
"""return loss"""
predict = self.calc(time) # (Batch * 1 * 2)
# teacher: (Batch * 2)
diff = predict - teacher.reshape(-1, 1, 2)
loss = F.sum(diff**2)
if self.train:
chainer.reporter.report({'loss': loss / len(time)})
else:
chainer.reporter.report({'validation/loss': loss / len(time)})
return loss
データセットの作成
[12/12追記] ここもGist版と違っていたので直しました
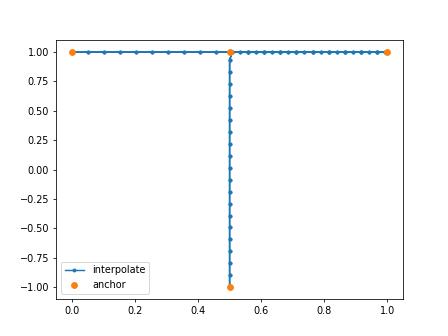
次は軌道の教師データを作っていきます。今回は"T"という文字を学習させます。いくつも点を打つのは面倒なので、主要な点を打った後はscipyの補間関数でデータを増やします。
from scipy import interpolate
anchor_t = np.array([ # これは手打ち
[0, 1],
[1, 1],
[0.5, 1],
[0.5, -1]
])
# Tの一筆書き
path_t_x = interpolate.interp1d(
np.linspace(0, 1, len(anchor_t)),
anchor_t[:,0])(np.linspace(0, 1, 60)).reshape(-1,1)
path_t_y = interpolate.interp1d(
np.linspace(0, 1, len(anchor_t)),
anchor_t[:,1])(np.linspace(0, 1, 60)).reshape(-1,1)
half_dataset_t = np.hstack((path_t_x, path_t_y))
# 一回の周期で元の位置に戻ってほしいので逆再生したやつを追加
dataset_t = np.vstack((half_dataset_t, half_dataset_t[::-1]))
学習
これをAdamに投げると
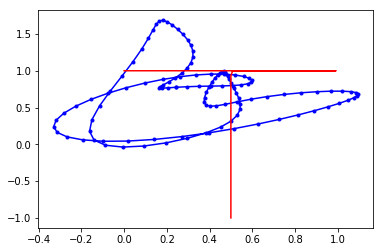
これが
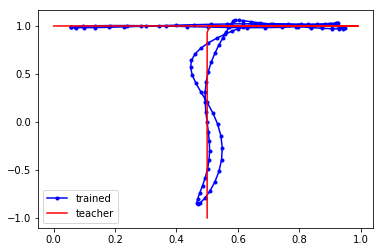
こうなりました(適当)。計50epoch、所要時間は100秒でした。ソースはMNISTのチュートリアルとほとんど同じなので省略します。
アニメーション
モデルから数値を取り出してやるだけです。補足することがあるとしたら、円運動の線形結合で表されるので惑星や衛星の順番は入れ替えても問題ないということぐらいでしょうか。なので公転半径を大きい順にソートすれば少し見栄えが良くなります。
コードはすごく汚いので結果だけ…(一応これも前述のGistに載せてます)
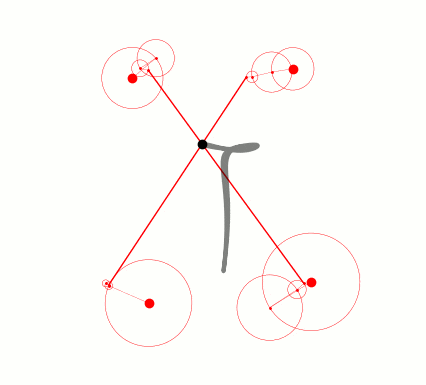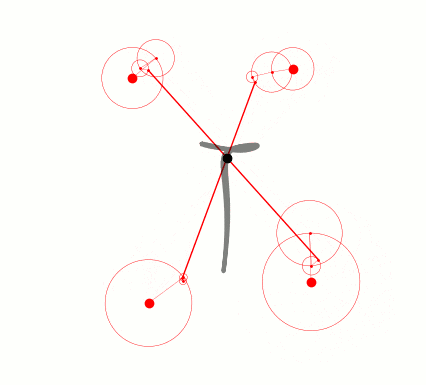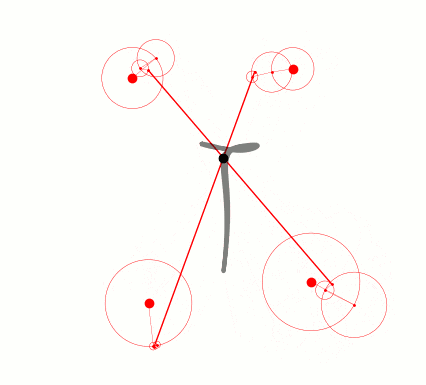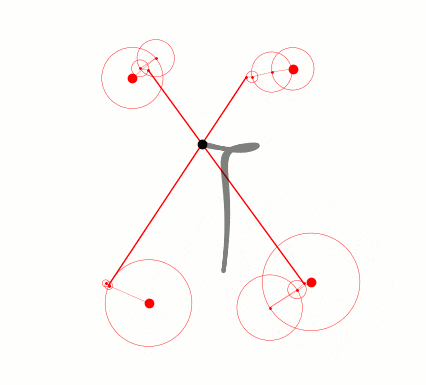
公転速度0の点がありますね…実質無いのと同じなので消してもいいのですが処理が面倒なので見なかったことにします。
おわりに
実はこれは駒場祭のネタでTSGの部誌にも書いたのですが、アドベントカレンダーをやるということでこれを機にもう少しだけ詳しく書いてみました。