雰囲気で覚える数理最適化 Maxcut問題

はじめに

数理最適化。なんとなくわかりましょうという記事。

数理最適化とは

From [WikiPedia]
[WikiPedia]: https://ja.wikipedia.org/wiki/%E6%95%B0%E7%90%86%E6%9C%80%E9%81%A9%E5%8C%96

数学の計算機科学やオペレーションズリサーチの分野における数理最適化（すうりさいてきか、英: mathematical optimization）とは、（ある条件に関して）最もよい元を、利用可能な集合から選択することをいう。

難しいことはおいておいて、数理最適化の世界では『もっともよい解』を判断する基準 や 『ある条件』を数式で表す。

それぞれの数式を以下のように呼ぶ。

• 『もっともよい解』を判断する基準の数式 = 目的関数
• といいます。『ある条件』は数式 = 制約式

数理最適化の例

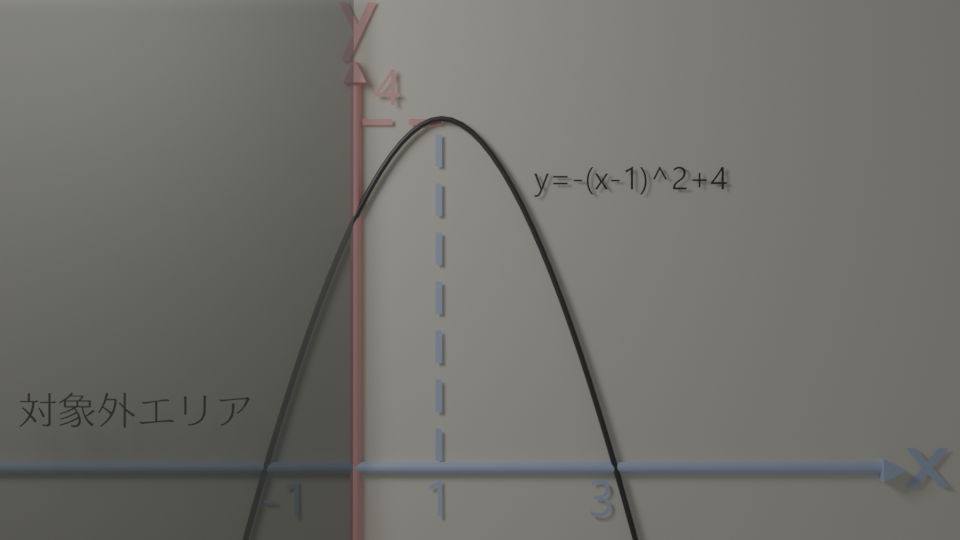
下図のような2次関数の最大値を求めたいときは、

目的関数： $y=-(x-1)^2 + 4 $ の最大化
制約式: $x \ge 0$

と表現します。

MaxCut問題

前置きはここまでにして、今回のネタのMaxCut問題を見ていきます。

再び From [WikiPedia MaxCut]
[WikiPedia MaxCut]: https://ja.wikipedia.org/wiki/%E3%82%AB%E3%83%83%E3%83%88_(%E3%82%B0%E3%83%A9%E3%83%95%E7%90%86%E8%AB%96)

グラフ理論において、グラフ$ G(V, E)$ の頂点 V の 2 分割 $(S, T)$ をカット（英: Cut）とよぶ。このとき、ある辺 $(u,v) \in E $の端点が $u \in S $かつ$v \in T$（有向グラフの場合 $u \in T$ でかつ $v \in S$ の場合もある）であるとき、この辺を「カットエッジ」と呼ぶ。

カットのサイズ (カットの重み) は、カットエッジの総数 (辺重みグラフの場合はカットエッジそれぞれの辺重みの総和) で表される。

最大サイズのカットを最大カットとよぶ。最大カット問題はNP完全であり、この証明は、最大充足可能性問題からの変換で得られる。

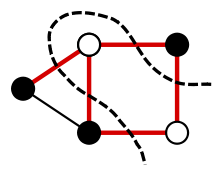
下図もWikiから流用させてもらいました。

簡単にいうと、ノードを二つのグループに分けて、エッジが異なるグループに属する際にカットされているとみなします。で、カットエッジの重みをすべて合計して最大にするという問題です。

解法

ノードの数ぶんだけ$x_i$を準備して、$-1,1$をとるものとします。
この時、カットエッジの総数は以下となります。これを最大化することが目的となるため、これが今回の目的関数です。

$$\sum_{(x_i,x_j)\in E} w_{x_i,x_j} (1-x_i \times x_j)^2$$

制約式はありません。

実装

無駄なコードも入っているため少し長くなっていますが、総当たりとD-Waveを用いた結果の比較です。

サンプルコード

import itertools
from pyqubo import Array,Sum,Constraint
from dwave.system import FixedEmbeddingComposite,EmbeddingComposite
import networkx as nx
from matplotlib import pyplot as plt
import time
import argparse
import random
import numpy as np

class MyTimer():
    '''
    時刻計測用 のクラス
    '''
    def __init__(self):
        self.set_timer()
            
    def set_timer(self):
        self.MY_TIMER = time.time()

    def get_timer(self):
        current_time = time.time()
        ret_time = current_time - self.MY_TIMER
        self.MY_TIMER = current_time
        return(ret_time)

def get_args():
    parser = argparse.ArgumentParser(description='This is sample argparse script')
    parser.add_argument('-n', '--node', default=7, type=int, help='This is number of nodes')
    parser.add_argument('-p', '--percentage', default=0.6, type=float, help='This is Probability for edge creation')
    parser.add_argument('-s', '--seed', default=0,type=int, help='This is seeds of random')

    return parser.parse_args()

class Problem():
    def __init__(self,n,p,seed):
        self.p = p
        self.n = n
        self.seed = seed
        self.G = nx.fast_gnp_random_graph(n,p,seed=seed)

        for v in self.G.nodes:
            if len(self.G.edges(v)) == 0:
                self.G.add_edge(v,random.randint(0,n))
        
        #重みづけ
        for (u,v) in self.G.edges:
            self.G.edges[u,v]['w'] = random.randrange(1,30,1)


        self.pos = nx.layout.spring_layout(self.G)

    def solve_dwave(self):
        timer = MyTimer()
        timer.set_timer()

        X = Array.create('X',shape=(self.n),vartype='SPIN')

        H0 = 0
        for (u,v) in self.G.edges:
            H0 -= (1 - X[u]*X[v])*self.G.edges[u,v]['w']

        model = H0.compile()
        bqm = model.to_dimod_bqm()
        bqm.normalize()

        response = EmbeddingComposite(DWaveSampler()).sample(bqm,num_reads=1000, chain_strength=2)
    
        result = model.decode_dimod_response(response,topk=1)
        optimized_v = result[0][0]['X']
        print(f"D-Wave size = {self.n} time = {timer.get_timer()} , Energy = {int(result[0][2]/2.0)}")

        self.v_group = []
        for i in range(self.n):
            self.v_group.append(int(optimized_v[i]))

        self.cutted = []
        for (u,v) in self.G.edges:
            if optimized_v[u] != optimized_v[v]:
                self.cutted.append([u,v])

    def show(self):
        plt.figure(figsize=(12,12),dpi=100)
        nx.draw_networkx(self.G,pos=self.pos)
        if len(self.cutted)>0:
            nx.draw_networkx_edges(self.G,self.pos,self.cutted,width=2,edge_color='r')
        edge_labels={}
        for (u,v) in self.G.edges:
            edge_labels[(u,v)] = self.G.edges[u,v]['w'] 
        nx.draw_networkx_edge_labels(self.G,self.pos,edge_labels=edge_labels)
        nx.draw_networkx_nodes(self.G,self.pos,nodelist=[idx for idx,v in enumerate(self.v_group) if v == 0],node_color='yellow')

        plt.show()

    def min_check(self):
        timer = MyTimer()
        timer.set_timer()
        min_value = 0
        for node_status in itertools.product((0,1),repeat=self.n):
            tmp_min = 0
            for (u,v) in self.G.edges:
                if node_status[u] != node_status[v]:
                    tmp_min -= self.G.edges[u,v]['w'] 
            
            if tmp_min < min_value:
                min_value = tmp_min

        print(f"Exact size = {self.n} ,time = {timer.get_timer()}, Energy = {min_value}")


if __name__ == '__main__':
    #args = get_args()
    #p = Problem(n=args.node,p=args.percentage,seed=args.seed)

    #p.solve_dwave()
    #p.show()
    for j in range(5):
        for i in range(5,26):
            p = Problem(n=i,p=args.percentage,seed=args.seed)
            p.solve_dwave()
            p.min_check()

実行結果

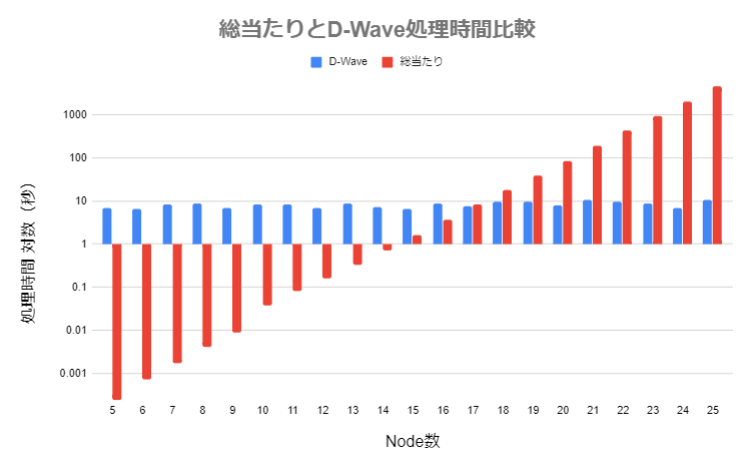
近似解を求める手法や、枝切り（あまり有効そうな感じがしませんが）を実施してない総当たりと比較するのもどうかと思いますが、処理時間の比較以下のような結果です。
※D-Wave側は1万回試行

D-Waveはほぼ時間が一定です。（さらに実際にD-Waveの装置内での処理は一瞬です）

#考察
・さすがに現在のCPUは優秀でノード数が少ない場合はごり押しパワーでなとかなる。
・ある一定のサイズを超えると、D-Waveが早くなる
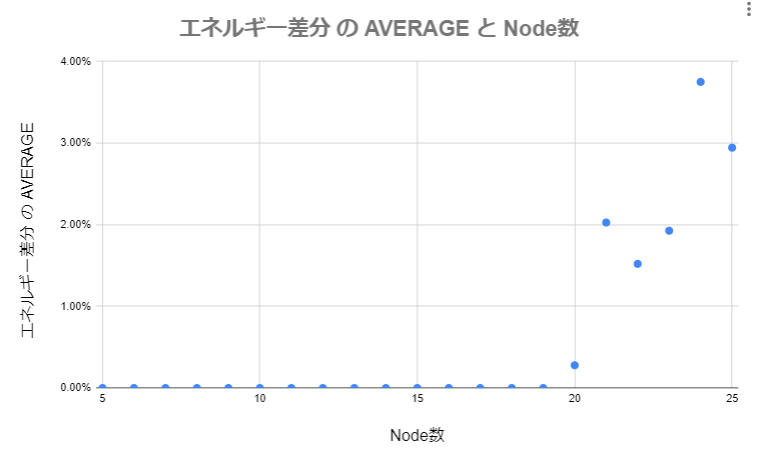
・ある一定サイズを超えるとD-Waveも正解が出なくなる。（最適解との誤差も大きくなりそう）
・回数を増やしてもD-Waveの処理時間は大きなインパクトはないが、前処理（Embedding）、通信時間、後処理に時間がかかるようになる。

非線形の問題であれば、D-Waveワンちゃんとも思える結果。

#その他
色々言われる量子アニーリングですが、AWS Bracketもリリースされましたし、面白そうなことができそうな気配はあるので、皆さんでレッツトライ！