LoginSignup
14
7

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@___monta___

ジョブショップ問題

Last updated at Posted at 2020-10-26

数理最適化勉強シリーズ

これまでにいくつか書いている数理最適の勉強のためのページです。
「今日から使える！ 組み合わせ最適化 離散問題ガイドブック」を参考に記載しています。
本にいくつか誤りを発見し、出版社に問い合わせしておりますが、反応なしです。ご注意ください。
※おそらくPage62の定式化も間違っています。

スケジューリング問題

様々な制限（制約）のもと、最もよい予定、順番を考えたいことが世の中にはたくさんあります。

バイトのシフトだったり、工場の生産の順番だったり。

そういうわけで、頭のいい人たちはそういった問題をスケジュール問題と呼び、最適化の対象として研究してきました。

tenchou_shift_woman.png

ジョブショップ問題（1機械問題）

例えば、いくつかの製品を作りたいとします。
それぞれの製品を作るためには、工場内の”すごい機械”を使用する必要があります。
”すごい機械”はすごいので、どんな製品でも作成できます。ただ、残念なことに工場にはこの”すごい機械”が1台しかありません。

koujou_machine.png

さて、ものを作るには色々な制約が発生します。

  • お客様の要望により、製品の製造は納期よりも前に完了する必要があります。
  • それぞれの材料が入荷できるタイミングもあるため、製品の製造は開始可能日以降に開始する必要があります。
  • 製品は製造するのにそれぞれ製造時間が決まっており、同時に2つの製品を製造することはできません。

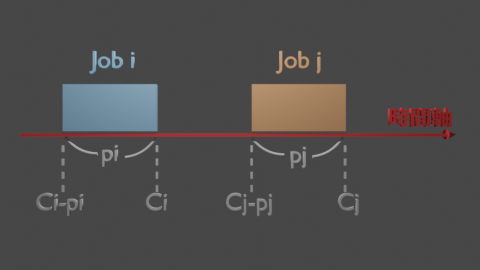
この後の説明を簡単にするために製品１に対して、納期を$d_1$、開始可能日を$r_1$、製造時間を$p_1$と表現します。
製品が1つや2つなら人間がスケジュールを考えるのは簡単です。では製品が100個、1000個あったら？

calender_shock_man.png

製品を製造する作業をジョブと呼び、製品が$n$個の時、どのようにスケジューリングすれば最も早く完了できるか考えます。

定式化の過程（数式での表現）

数理最適化では、問題をどのように数式で表現するかがキモになります。
考え方としては、決めたいことを変数として定義し、その変数を用いて様々な制約を数式で表現します。

変数の定義

この問題では

  • ジョブ$i$をジョブ$j$よりも前に実施する場合$x_{i,j}$ = 1
  • ジョブ$i$をジョブ$j$よりも後に実施する場合$x_{i,j}$ = 0

となる変数$x_{i,j}$を定義します。ジョブ$i$とジョブ$j$の間に別のジョブがあっても構いません。
この変数は単に2つのジョブの前後関係だけを表します。

ジョブの終了時間（定義はこうだけど、使わないかも）

変数$x_{i,j}$を用いることで、製品$i$の製造が完了するタイミング、つまりジョブの終了時間$c_i$は以下のいずれかの遅いほうとして定義することができます。

  • 最速の場合、ジョブ$i$の開始可能日$r_i$から製造時間$p_i$後なので、$r_i$+$p_i$
  • 他のジョブとの兼ね合いで最速で完了できない場合は、ジョブ$i$よりも前に実行されるなかでも最も最後に終わるジョブ$j'$にジョブ$i$の製造時間を足したものとなる。
    $$\max_{j' \in V| x_{i,j'}=0} c_{j'} + p_i$$

上記をまとめて記載すると以下になります。

$$c_i = \max \{r_i,\max_{j' \in V| x_{i,j'}=0 } c_{j'} \} + p_i$$

納期の制約

製造が完了するタイミングは納期$d_i$の前でなければなりません。つまり、

式(1): $c_i \le d_i $

開始タイミング、製造時間

$c_i$は必ず、開始可能日$r_i$から製造時間$p_i$を経過した後となります。（そうでなければ準備ができていないのにジョブを開始したことになりルール違反）。つまり、

式(2): $c_i \ge r_i + p_i$

複数のジョブの開始タイミングと終了タイミング

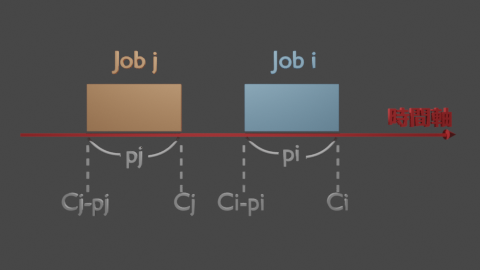
ジョブ$i$がジョブ$j$よりも前に実行される場合、ジョブ$i$の終了時間は、ジョブ$j$の開始時間よりも前になるため、
$c_i \le c_j - p_j$

jobij.png

同様に、ジョブ$i$がジョブ$j$よりも後に実行される場合、ジョブ$i$の開始時間は、ジョブ$j$の終了時間よりも後ろになるため、
$c_j \le c_i - p_i$

jobji.png

両方が成り立つ場合は、普通に制約式が2つを記載すればよいのですが、この二つの制約式はどちらか一方のみ（つまりOR）が成り立ちます。このままでは問題が解けないので、ちょっとしたテクニックを使います。（この方法はbig-Mと呼ばれる方法で、数理最適化ではメジャーな方法なようです）

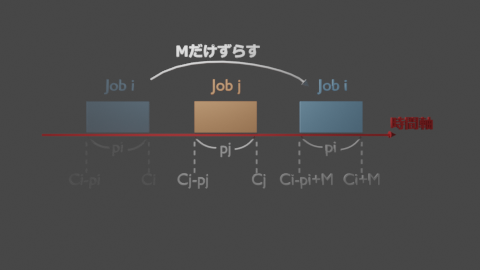
ジョブ$i$がジョブ$j$よりも前に実行されるときにジョブ$i$をずっと右側、つまり時間的に後ろにずらしましょう。ずらす時間をMとすると、十分Mが大きければ、なんと！！ ジョブ$j$の終了時間はジョブ$i$の開始時間よりも前になります！

これだけ聞くと、アホらしい話ですが、重要なテクニックです。

jobijM.png

式で表すと、ジョブ$i$がジョブ$j$よりも前に実行でも大きいMを用いることで、以下を満たします。
$c_j \le c_i - p_i + M$

整理しましょう。

ジョブの順序 $x_{i,j}$ 制約式
ジョブ$i$がジョブ$j$よりも前 1 $c_j \le c_i - p_i + M$
ジョブ$i$がジョブ$j$よりも後 0 $c_j \le c_i - p_i$

鋭い人はピンときたかもしれませんが、$x_{i,j}$を使うと、上の二つの式をまとめることができます。
式(3): $c_j \le c_i - p_i + M*x_{i,j}$

同様に、
jobjiM.png

ジョブの順序 $x_{i,j}$ 制約式
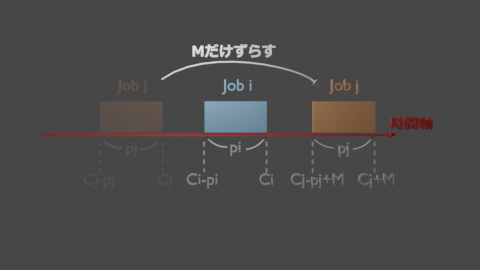
ジョブ$i$がジョブ$j$よりも前 1 $c_i \le c_j - p_j$
ジョブ$i$がジョブ$j$よりも後 0 $c_i \le c_j - p_j + M$

$x_{i,j}$用いて、上記2式をまとめて、
式(4): $c_i \le c_j - p_j + M*(1-x_{i,j})$
とまとめることができます。

目的関数

色々頑張ったので、目的を忘れそうですが、目的は「最も早く完了」させることです。
数理最適化では、何かを最小化、または最大化するということを数式で表します。
ジョブ$i$の終了時間が$c_i$なので、最後にジョブが終了する時間、つまり$c_1,c_2,c_3....c_n$のうち、最大の数字を最も小さくすることが目的です。

ここにももう一つ素晴らしいトリックがあります。最終のジョブの終了時間を$z$とすると、すべてのジョブに対して以下を定義し、$z$の最小化を目的関数とすることで、最も早く完了させる時間$z$を知ることができます。
目的関数： $zの最小化$

式(5): $c_i \le z $

定式化のまとめ

さて、これまでの内容をまとめましょう。

目的関数は以下です。
$zの最小化$

制約式は以下となります。
式(1): $c_i \le d_i $
式(2): $c_i \ge r_i + p_i$
式(3): $c_j \le c_i - p_i + Mx_{i,j}$
式(4): $c_i \le c_j - p_j + M(1-x_{i,j})$
式(5): $c_i \le z $

実装

python + Pulp で実装すると以下のようになります。
*問題設定によっては解けない場合があるので、ランダムシードを変える、Vを変えるTERMを変えるなど人間が努力してください。

from pulp import LpProblem,LpConstraint,LpVariable,LpBinary,LpInteger,LpStatus,PULP_CBC_CMD
from random import randint,seed

# Define Jobs
class job():
    def __init__(self,term,max_p):
        self.p = randint(1,max_p)
        self.r = randint(0,term-self.p*2)
        self.d = randint(self.r+self.p,term)

    def print(self):
        print(f"r={self.r},d={self.d},p={self.p}")

    @staticmethod
    def check_conflict(j1,j2s):
        flag = False

        for j2 in j2s:
            #j1 start earlier than j2
            if j2.d-j2.p < j1.r+j1.p and j1.d-j1.p < j2.r+j2.p:
                flag = True
                break
        
        return flag

class jobs():
    def __init__(self,num,term,max_p):
        self.j = []

        for i in range(num):
            conflict_flag = True
            while conflict_flag:
                tmp_j = job(term,max_p)
                conflict_flag = job.check_conflict(tmp_j,self.j)

            self.j.append(tmp_j)

    def print(self):
        for idx,j in enumerate(self.j):
            print(f"job {idx},",end="")
            j.print()

    def get_r(self,i):
        return self.j[i].r

    def get_p(self,i):
        return self.j[i].p

    def get_d(self,i):
        return self.j[i].d


        
if __name__ == "__main__":
    #Setting Random Seed
    seed(1)

    #Job number
    V = 20
    TERM = 100

    #Define Problem
    myjobs = jobs(V,TERM,5)
    myjobs.print()

    #Define Pulp Problem 
    p = LpProblem("OneMachineProblem")

    ##########################
    #Define Variables

    #Order between two Jobs
    #x[i][j] = 1 mean job i start before job j 
    #x[i][j] = 0 mean job i start after job j 
    x = LpVariable.dict("x",indexs=(range(V),range(V)),lowBound=0,upBound=1,cat=LpBinary)

    #End time of jobs
    c = LpVariable.dict("c",indexs=(range(V)),lowBound=0,upBound=TERM,cat=LpInteger)

    #to minimize end
    y = LpVariable("y",lowBound=0,upBound=TERM,cat=LpInteger)

    ##########################
    #Ojbective is minimize end time
    p += y

    ##########################
    #subject to...

    #define y is later than all end time(c)
    for i in range(V):
        p += c[i] <= y

    #Job End timing(c) is after ready time(r)+producing time(p)
    for i in range(V):
        p += c[i] >= myjobs.get_r(i) + myjobs.get_p(i)
    
    #Job End tiing(c) is earlier than delivery time(d)
    for i in range(V):
        p += c[i] <= myjobs.get_d(i)

    # #2 Jobs Condition    
    for i in range(V):
        for j in range(i+1,V):
            p += c[i] <= c[j] - myjobs.get_p(j) + TERM*(1-x[(i,j)])

    for i in range(V):
        for j in range(i+1,V):
            p += c[j] <= c[i] - myjobs.get_p(i) + TERM*x[(i,j)]
    
    print("\nSolving...")
    solver=PULP_CBC_CMD(msg=0)
    stat=p.solve(solver)
    print(f"  Done: {LpStatus[stat]}")


    if stat == 1:
        print("\nResult:")
        for i in range(V):
            print(f"job {i}, {c[i].value() - myjobs.get_p(i) } , {c[i].value()}")

        print(f"Best Delivery = {y.value()}")

実行時の出力結果は以下となります。r,d,pはそれぞれ各ジョブの開始可能日、納期、製造期間です。
OptimalはPulpのSolve実行結果で最適化されていることを意味します。

解けていますね！

実行結果
job 0,r=72,d=99,p=2
job 1,r=32,d=48,p=1
job 2,r=57,d=91,p=4
job 3,r=26,d=42,p=4
job 4,r=3,d=56,p=4
job 5,r=77,d=81,p=4
job 6,r=34,d=84,p=4
job 7,r=75,d=80,p=2
job 8,r=3,d=8,p=3
job 9,r=83,d=84,p=1
job 10,r=87,d=94,p=4
job 11,r=92,d=96,p=4
job 12,r=28,d=89,p=5
job 13,r=70,d=81,p=4
job 14,r=29,d=60,p=3
job 15,r=37,d=100,p=4
job 16,r=53,d=89,p=1
job 17,r=23,d=61,p=1
job 18,r=95,d=98,p=1
job 19,r=54,d=91,p=5

Solving...
  Done: Optimal

Result:
job 0, 81.0 , 83.0
job 1, 40.0 , 41.0
job 2, 67.0 , 71.0
job 3, 32.0 , 36.0
job 4, 36.0 , 40.0
job 5, 77.0 , 81.0
job 6, 63.0 , 67.0
job 7, 75.0 , 77.0
job 8, 3.0 , 6.0
job 9, 83.0 , 84.0
job 10, 87.0 , 91.0
job 11, 92.0 , 96.0
job 12, 41.0 , 46.0
job 13, 71.0 , 75.0
job 14, 29.0 , 32.0
job 15, 53.0 , 57.0
job 16, 57.0 , 58.0
job 17, 23.0 , 24.0
job 18, 96.0 , 97.0
job 19, 58.0 , 63.0
Best Delivery = 97.0

Happy 最適化 Life！

Pulpなどを用いて楽しい数理最適化Lifeを！

14
7
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
14
7

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?