数理最適化とは
From [WikiPedia]
[WikiPedia]: https://ja.wikipedia.org/wiki/%E6%95%B0%E7%90%86%E6%9C%80%E9%81%A9%E5%8C%96
数学の計算機科学やオペレーションズリサーチの分野における数理最適化(すうりさいてきか、英: mathematical optimization)とは、(ある条件に関して)最もよい元を、利用可能な集合から選択することをいう。
難しいことはおいておいて、数理最適化の世界では『もっともよい解』を判断する基準 や 『ある条件』を数式で表す。
それぞれの数式を以下のように呼ぶ。
- 『もっともよい解』を判断する基準を表す数式 = 目的関数
- 『ある条件』を表す数式 = 制約式
最小重み完全マッチング問題
各辺$ e \in E$の重み$w(e)$が与えられている2部グラフ$G=(V,E) $に対して、重みの和$\sum_{e \in M} w(e)$が最小の完全マッチング$M$を求めよ。
| 最小重み完全マッチング例 | 説明 |
|---|---|
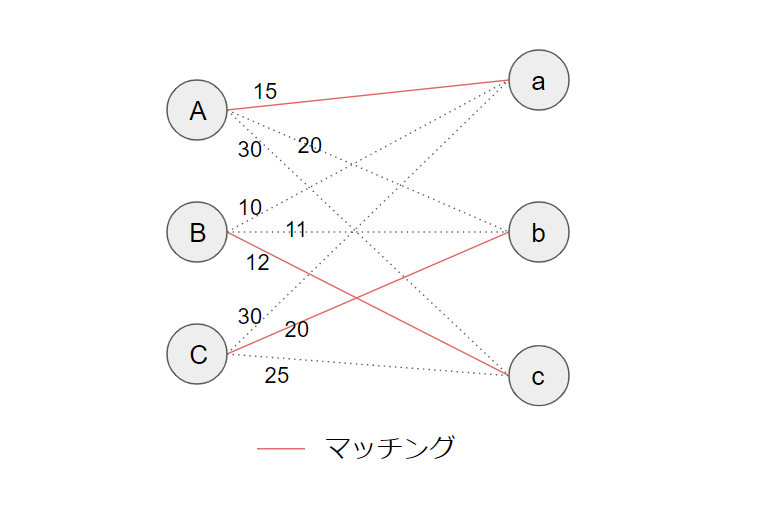 |
"最小"はマッチングの辺の重みの合計が最小となること。また”完全マッチング”は選択したエッジの集合が端点を共有しておらず、すべてのノードを含んでいること。 |
日本語で書き下すと、左右に同じ数の〇が存在する。左右の〇は線でつながれている。線にはそれぞれ点数が決められている。いくつか線を選んですべての〇を含むようにし、点数の合計を最小にする選び方を求める。(ただし、一つの〇から複数の線が出てはいけない)
定式化
ある辺$e$がマッチングの要素である場合、1、そうでない場合0となる変数$x(e)$を定義すると、最小重み完全マッチング問題は以下のように表現できる。
目的関数
$$minimize \sum_{e\in E} w(e)x(e)$$
制約条件
$$\sum_{e\in \delta (v)} x(e) = 1 \quad (\forall v \in V)$$
$$x(e) = \{ 0,1 \} \quad \quad(\forall e \in E)$$
実装
問題を簡単めにするとプログラムも非常にシンプル
from pulp import LpProblem,LpVariable,LpBinary,lpSum,value
import random
import numpy as np
from itertools import product
p = LpProblem("mwpmp")
# 問題作成
random.seed(10)
PSIZE = 100
w = np.random.uniform(0,1,size=(PSIZE,PSIZE))
x = LpVariable.dict(name="x",indexs=(range(PSIZE),range(PSIZE)),cat=LpBinary)
p += lpSum(x[i,j]*w[i,j] for i,j in product(range(PSIZE),range(PSIZE)))
for i in range(PSIZE):
p += lpSum(x[i,j] for j in range(PSIZE)) == 1
p += lpSum(x[j,i] for j in range(PSIZE)) == 1
p.solve()
for i,j in product(range(PSIZE),range(PSIZE)):
if value(x[i,j]) == 1:
print(f"Matching ({i},{j})")
せっかくなのでCPLEXも試してみましょう。
IBMのCPLEXのページからフリーバージョンをダウンロード
https://www.ibm.com/jp-ja/products/ilog-cplex-optimization-studio
Linux版をダウンロードして、実行権限をつけて実行です。
chmod +x cos_installer_preview-20.1.0.0.R1-CC8CWML-linux-x86-64.bin
./cos_installer_preview-20.1.0.0.R1-CC8CWML-linux-x86-64.bin
インストールしたバージョンとインストール先は以下のような感じ。
Product Name:
IBM ILOG CPLEX Optimization Studio Community Edition 20.1.0
Install Folder:
/opt/ibm/ILOG/CPLEX_Studio_Community201
インストール後にPythonAPIインストール方法も表示されるので、念のため従っておきます。
python3 /opt/ibm/ILOG/CPLEX_Studio_Community201/python/setup.py install
先ほどのプログラムでSolverをデフォルトのCOIN|ORからCBCに変更します。
修正箇所は以下
solver=CPLEX_CMD()
p.solve(solver)
実行すると以下のようなログが出力されます。
きっちり16Thread認識しているようですし、問題が簡単すぎて瞬間的に(0.03秒?)完了していますね。
※このレベルだとCOIN|ORでも0.02秒と表示されるので、能力差が不明です。
CPLEX> Problem '/tmp/7434b38613994b109f4d85bdebd633fe-pulp.lp' read.
Read time = 0.00 sec. (0.05 ticks)
CPLEX> Version identifier: 20.1.0.0 | 2020-11-11 | 9bedb6d68
Found incumbent of value 13.606922 after 0.00 sec. (0.07 ticks)
Found incumbent of value 2.663959 after 0.00 sec. (0.10 ticks)
Tried aggregator 1 time.
Reduced MIP has 60 rows, 900 columns, and 1800 nonzeros.
Reduced MIP has 900 binaries, 0 generals, 0 SOSs, and 0 indicators.
Presolve time = 0.00 sec. (1.09 ticks)
Probing time = 0.00 sec. (2.36 ticks)
Tried aggregator 1 time.
Reduced MIP has 60 rows, 900 columns, and 1800 nonzeros.
Reduced MIP has 900 binaries, 0 generals, 0 SOSs, and 0 indicators.
Presolve time = 0.00 sec. (1.10 ticks)
Probing time = 0.00 sec. (2.36 ticks)
Clique table members: 60.
MIP emphasis: balance optimality and feasibility.
MIP search method: dynamic search.
Parallel mode: deterministic, using up to 16 threads.
Root relaxation solution time = 0.01 sec. (0.46 ticks)
Nodes Cuts/
Node Left Objective IInf Best Integer Best Bound ItCnt Gap
* 0+ 0 2.6640 0.0000 100.00%
* 0+ 0 2.5791 0.0000 100.00%
* 0+ 0 1.9340 0.0000 100.00%
* 0+ 0 1.8848 0.0000 100.00%
* 0+ 0 1.6418 0.0000 100.00%
* 0+ 0 1.5647 0.0000 100.00%
* 0+ 0 1.5158 0.0000 100.00%
* 0 0 integral 0 1.3265 1.3265 22 0.00%
Elapsed time = 0.03 sec. (8.89 ticks, tree = 0.00 MB, solutions = 8)
Root node processing (before b&c):
Real time = 0.03 sec. (8.97 ticks)
Parallel b&c, 16 threads:
Real time = 0.00 sec. (0.00 ticks)
Sync time (average) = 0.00 sec.
Wait time (average) = 0.00 sec.
------------
Total (root+branch&cut) = 0.03 sec. (8.97 ticks)
Solution pool: 9 solutions saved.
MIP - Integer optimal solution: Objective = 1.3264513471e+00
Solution time = 0.03 sec. Iterations = 22 Nodes = 0
Deterministic time = 8.97 ticks (299.00 ticks/sec)
CPLEX> MILP problem relaxed to LP with fixed integer variables using
incumbent solution.
CPLEX> Version identifier: 20.1.0.0 | 2020-11-11 | 9bedb6d68
Tried aggregator 1 time.
LP Presolve eliminated 60 rows and 900 columns.
All rows and columns eliminated.
Presolve time = 0.00 sec. (0.22 ticks)
Dual simplex - Optimal: Objective = 1.3264513471e+00
Solution time = 0.00 sec. Iterations = 0 (0)
Deterministic time = 0.30 ticks (304.04 ticks/sec)
CPLEX> Solution written to file '/tmp/7434b38613994b109f4d85bdebd633fe-pulp.sol'.
IBMらしく、EclipseIDEでの開発も可能です。
