前書き
本記事は
量子コンピューター Advent Calendar 2020
の13日目です。
重要なこと書き忘れたので追記!
数理最適化とは
From [WikiPedia]
[WikiPedia]: https://ja.wikipedia.org/wiki/%E6%95%B0%E7%90%86%E6%9C%80%E9%81%A9%E5%8C%96
数学の計算機科学やオペレーションズリサーチの分野における数理最適化(すうりさいてきか、英: mathematical optimization)とは、(ある条件に関して)最もよい元を、利用可能な集合から選択することをいう。
難しいことはおいておいて、数理最適化の世界では『もっともよい解』を判断する基準 や 『ある条件』を数式で表す。
それぞれの数式を以下のように呼ぶ。
- 『もっともよい解』を判断する基準を表す数式 = 目的関数
- 『ある条件』を表す数式 = 制約式
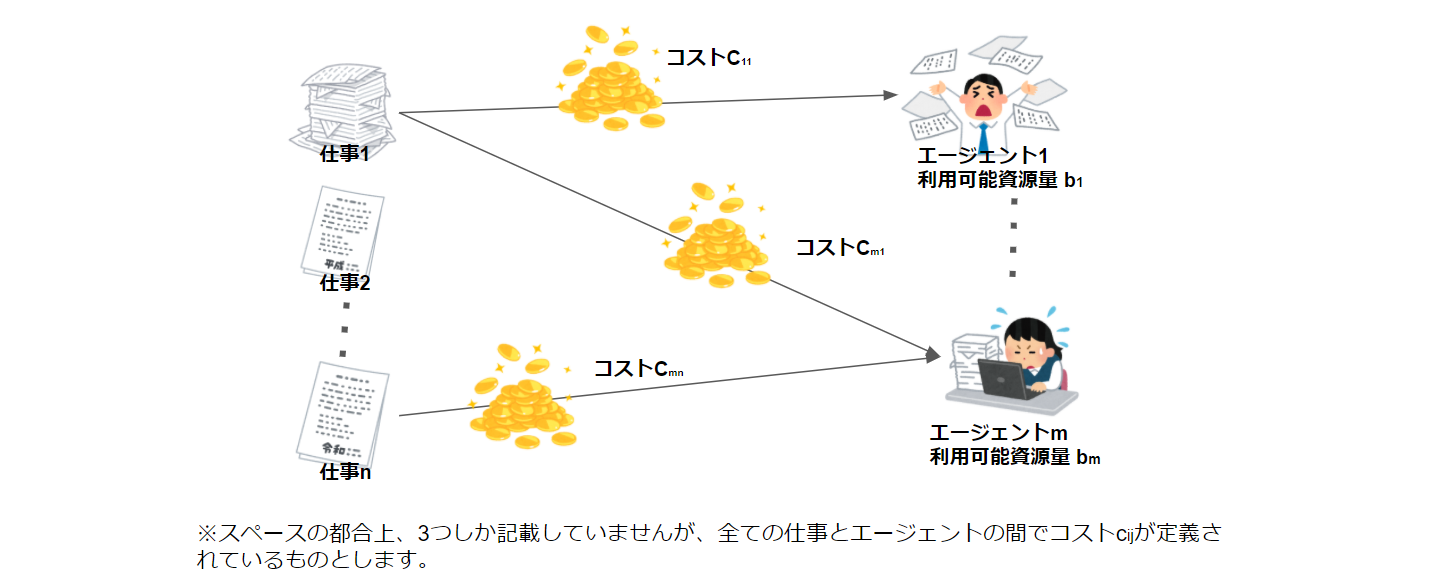
一般化割り当て問題とは
与えられたいくつかの仕事をエージェントに割り当てるとき、割り当てに伴うコストの総和を最小化する問題を一般化割り当て問題と呼びます。
問題定義
$n$個の仕事$J= \{1,2, \cdots ,n \}$と$m$人のエージェント$I=\{1,2, \cdots ,m\}$に対して、仕事$j \in J$をエージェント$i \in I$に割り当てたときのコスト$c_{ij}$と資源の要求量$a_{ij}(\ge 0)$、おおよび各エージェント$i \in I$の利用可能資源量$b_i(>0)$が与えられている。それぞれの仕事を必ずいずれかの1つのエージェントに割り当てなくてはならず、また、各エージェントに割り当てられた仕事の壮士原料が、そのエージェントの利用可能資源を超えないようにしなくてはいけない。この時、割り当てに伴うコストの総和を最小化するような割り当てを求めよ。
イメージ図
定式化
変数定義
仕事$j$をエージェント$i$に割り当てるときに$1$,そうでないときに$0$をとる変数$x_{ij}$を定義する
目的関数
目的は「割り当てに伴うコストの総和を最小化する」ことなので、以下のように定義できる。
$$\sum_{i \in I} \sum_{j \in J}c_{ij} x_{ij} \quad 最小化$$
制約式
割り当てられた仕事の資源要求量がエージェントの利用資源量を超えないように。
$$ \sum_{j \in J} a_{ij} x_{ij} \le b_i, \quad \forall i \in I \quad 制約式(1)$$
全ての仕事を、いずれかのエージェントには割り当てる必要があるので。
$$ \sum_{i \in I} x_{ij} = 1, \quad \forall j \in J,\quad 制約式(2)$$
$x$は割り当てを定義するバイナリ変数なので。
$$ x_{ij} \in \{ 0,1 \}, \quad \forall i \in I, \forall j \in J \quad 制約式(3)$$
比較
定式化などの実装を間違える可能性もあるため、まずは線形計画として、こなれた数理最適化Solverで解きます。
問題なさそうでしたら、D-Waveで解いてみます。
線形計画Solver
線形計画Solver 実装
迷うポイントがないので、サクッとPulpで実装。
import pulp
import numpy as np
import random
from itertools import product
import pandas as pd
# ランダム設定 同じ条件で評価できるように
random.seed(1)
np.random.seed(1)
# 仕事の数m、エージェント数n
m=10
n=5
# 仕事の最大サイズ(調整用)
JOB_SIZE=10
# 仕事jの資源要求量
a = np.random.randint(2,JOB_SIZE,size=(n,m))
# エージェントの利用可能資源量
b = np.random.randint(3,JOB_SIZE*2,size=n)
# コスト
c = np.random.randint(1,10,size=(n,m))
################################################################################
##### Pulpで解く
p = pulp.LpProblem("AssignmentProblem")
x = pulp.LpVariable.dict("x",indexs=(range(n),range(m)),lowBound=0,upBound=1,cat=pulp.LpBinary)
# 目的関数定義
p += pulp.lpSum([x[(i,j)]*c[i,j] for i,j in product(range(n),range(m))])
# エージェントの利用可能資源量を超えない
for i in range(n):
p += pulp.lpSum([x[(i,j)]*a[i,j] for j in range(m)]) <= b[i]
# 全ての仕事をエージェントに割り振る
for j in range(m):
p += pulp.lpSum([x[(i,j)] for i in range(n)]) == 1
p.solve()
# 解が最適解であれば結果を表示
if p.status == 1:
print("Optimization Result by Pulp")
cols = []
assigned_agents=[]
for j in range(m):
cols.append(f"JOB{j}")
assigned_agents.append(int(sum(i*x[(i,j)].value() for i in range(n))))
df = pd.DataFrame([assigned_agents],columns=cols,index=["result"])
print(df)
print(f"Value = {pulp.value(p.objective)}")
elif p.status == -1:
print("実行不能解")
exit(0)
線形計画Solver 実行結果
問題規模も小さいので速攻答えが出ます。
$ /usr/bin/python3 AssignmentProblem_pulp.py
Result - Optimal solution found
Objective value: 25.00000000
Enumerated nodes: 0
Total iterations: 0
Time (CPU seconds): 0.01
Time (Wallclock seconds): 0.01
Option for printingOptions changed from normal to all
Total time (CPU seconds): 0.01 (Wallclock seconds): 0.01
Optimization Result by Pulp
JOB0 JOB1 JOB2 JOB3 JOB4 JOB5 JOB6 JOB7 JOB8 JOB9
result 1 4 1 2 3 1 0 4 2 3
Value = 25.0
D-Wave Advantage
D-Waveで実装する際には、このような問題でも以下ような悩みがあります。
- イジングモデルのみで表現する必要があるため、一般的にはペナルティ法を用いて制約条件を目的関数にひっくるめます。
- 不等号の表現が難しい。補助スピンを用いて表現することが多いが、スピンが増えるため、正解が出にくくなる。
- もともとも目的関数と、制約式(ペナルティ項)のバランスをとることが難しい。
1) イジング式での表現
ポイントとなるコードだけ抜き出して説明します。
ここではH1にもともとの目的関数、H2にエージェントの利用可能資源量を超えない(制約式(1))、H3にすべての仕事を割り振る(制約式(2))を定義して、一つの式にしています。
各項のバランスを後で整えることができるように、PyquboのPlaceholderを使っています。(最終的にはPlaceholderがなんらかの数字になる)
# 目的関数定義相当
H1 = Sum(0,m,lambda j: Sum(0,n,lambda i: x[i][j]*c[i,j]))
# エージェントの利用可能資源量を超えない
H2 = Sum(0,n,lambda i: Constraint(Sum(0,m,lambda j: x[(i,j)]*a[i,j] +y[i] - b[i])**2,f"Agent Resource {i}"))
# 全ての仕事をエージェントに割り振る
H3 = Sum(0,m,lambda j: Constraint(Sum(0,n,lambda i: x[i][j]-1)**2 ,f"Job{j}"))
H = Placeholder("balancer1")*H1 + Placeholder("balancer2")*H2 + Placeholder("balancer3")*H3
2) 不等号の表現
以下の不等式で定義された制約条件を、目的関数に取り込むことを考えます。
$$ \sum_{j \in J} a_{ij} x_{ij} \le b_i, \quad \forall i \in I \quad 制約式(1)$$
エージェントの請け負った仕事は$\sum_{j \in J} a_{ij} x_{ij}$ で表せます。目的関数としては、$\sum_{j \in J} a_{ij} x_{ij}$ が$0$から$b_i$であれば、0となる式を作る必要があります。
ここで、$0$から$b_i$まで変化する$y_i$を定義し、以下のような式を考えると、制約式(1)を満たすときには0,それ以外は正の数となります。(こういった変数をスラック変数と呼びます)
$(\sum_{j \in J} a_{ij} x_{ij} + y_i - b_i)^2$
コードは以下のような実装となります。Constraintを用いることにより、式が0になったかどうかを自動的にチェックできます。(満たさなかった場合は、何が満たさなかったかを返す)
# エージェントの利用可能資源量を超えない
H2 = Sum(0,n,lambda i: Constraint(Sum(0,m,lambda j: x[(i,j)]*a[i,j] +y[i] - b[i])**2,f"Agent Resource {i}"))
3) 目的関数と、制約式(ペナルティ項)のバランス
これは難しい課題です。簡単な問題であれば、それぞれの式がどれくらいの値となるかでバランスにあたりが付きますが、最適解が出やすいかというと、また別の問題です。
また項によっては絶対に満たさなくてはならない項目(ハード制約)と満たされるとより良い項目(ソフト制約)などの違いもあります。
が、まずは解が出ないことには始まりません。私は、まずはパラメータを変えながら繰り返しサンプリングをして実行可能回が出る回数を目安にバランスを探ています。
シェルを回して適当に探索してもいいのですが、最近は少し工夫をしてOptunaを使ったりしています。
https://github.com/optuna/optuna
ただし、実際のところD-Waveはパラメータが同じでも実行毎にかなり結果が異なるため、あまりあてになりません。
D-WaveAdvanage 実装
実際にOptunaを組み込んでパラメータ最適化したのち、結果を見るコードが以下です。
※後述しますが、一度も実行可能回が求まらなかったため、出力が極めて適当です。
from pyqubo import Array,Sum,Constraint,Placeholder,OneHotEncInteger,UnaryEncInteger,LogEncInteger
from dwave.system import EmbeddingComposite,DWaveSampler,LeapHybridSampler
import numpy as np
import random
from itertools import product
import pandas as pd
import optuna
# ランダム設定 同じ条件で評価できるように
random.seed(1)
np.random.seed(1)
# 仕事の数m、エージェント数n
m=10
n=5
# 仕事の最大サイズ(調整用)
JOB_SIZE=10
# 仕事jの資源要求量
a = np.random.randint(2,JOB_SIZE,size=(n,m))
# エージェントの利用可能資源量
b = np.random.randint(3,JOB_SIZE*2,size=n)
# コスト
c = np.random.randint(1,10,size=(n,m))
################################################################################
### D-Waveで解く
## パラメータ探索用
def objective(trial):
b1 = trial.suggest_uniform('b1',0.0,20)
b2 = trial.suggest_uniform('b2',0.0,20)
b3 = trial.suggest_uniform('b3',0.0,20)
def_dict = {"balancer1":b1,"balancer2":b2,"balancer3":b3,"IntChain":1.0}
bqm = model.to_dimod_bqm(feed_dict=def_dict)
sampler = EmbeddingComposite(DWaveSampler(sampler="Advantage_system1.1"))
responses = sampler.sample(bqm,num_reads=5000)
solutions = model.decode_dimod_response(responses,feed_dict=def_dict)
cnt = 0
for idx,sol in enumerate(solutions):
if len(sol[1]) < 10:
cnt += responses.record[idx][2]
return cnt
# 定義上書き!
x = Array.create('x',shape=(n,m),vartype="BINARY")
# 不等号表現用の補助スピン
y = []
for i in range(n):
#y.append(OneHotEncInteger(f"y{i}",lower=0,upper=JOB_SIZE*2,strength=Placeholder("IntChain")))
y.append(LogEncInteger(f"y{i}",lower=0,upper=JOB_SIZE*2))
# 目的関数定義相当
H1 = Sum(0,m,lambda j: Sum(0,n,lambda i: x[i][j]*c[i,j]))
# エージェントの利用可能資源量を超えない
H2 = Sum(0,n,lambda i: Constraint(Sum(0,m,lambda j: x[(i,j)]*a[i,j] +y[i] - b[i])**2,f"Agent Resource {i}"))
# 全ての仕事をエージェントに割り振る
H3 = Sum(0,m,lambda j: Constraint(Sum(0,n,lambda i: x[i][j]-1)**2 ,f"Job{j}"))
H = Placeholder("balancer1")*H1 + Placeholder("balancer2")*H2 + Placeholder("balancer3")*H3
model = H.compile()
# パラメータ探索
study = optuna.create_study(storage='sqlite:///example.db',study_name=f"m{m}n{n}_advantage",load_if_exists=True)
study.optimize(objective, n_trials=100)
b1 = study.best_params["b1"]
b2 = study.best_params["b2"]
b3 = study.best_params["b3"]
def_dict = {"balancer1":b1,"balancer2":b2,"balancer3":b3,"IntChain":10.0}
bqm = model.to_dimod_bqm(feed_dict=def_dict)
sampler = EmbeddingComposite(DWaveSampler(sampler="Advantage_system1.1"))
responses = sampler.sample(bqm,num_reads=1000)
solutions = model.decode_dimod_response(responses,feed_dict=def_dict)
cnt = 0
for sol in solutions:
if len(sol[1]) < 10:
weight_const_flag = False
for i in range(n):
if sum(sol[0]['x'][i][j] * a[i,j] for j in range(m)) > b[i]:
weight_const_flag = True
#エージェントのリソースを超えている場合は答え候補を無視
if (weight_const_flag) :
continue
print(sol[0])
print(sol[1])
print(sol[2])
cnt += 1
print("No penalty answer count is",cnt)
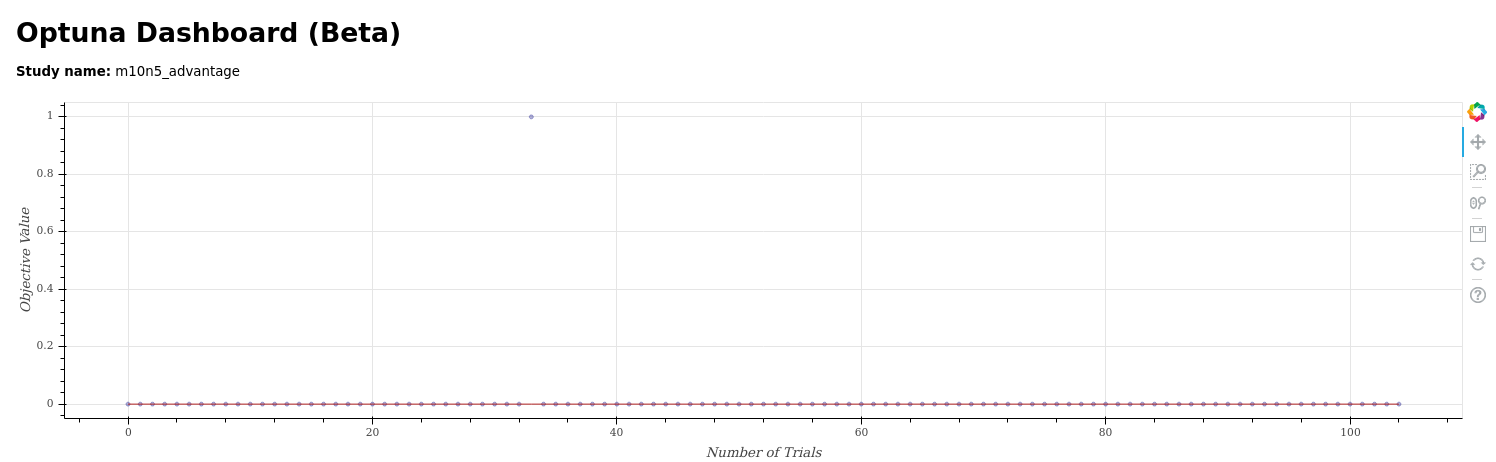
D-Wave Advanage 実行結果
最適解ではなく、実行可能回が出た回数が縦軸方向なのですが、0回が並んでおり、全く解けていないことがわかります。
※最適解でなく、実行可能回の出現回数です。
なお、1回の試行は毎回5000回のSamplingを行っており、十分な回数を実施しているつもりです。
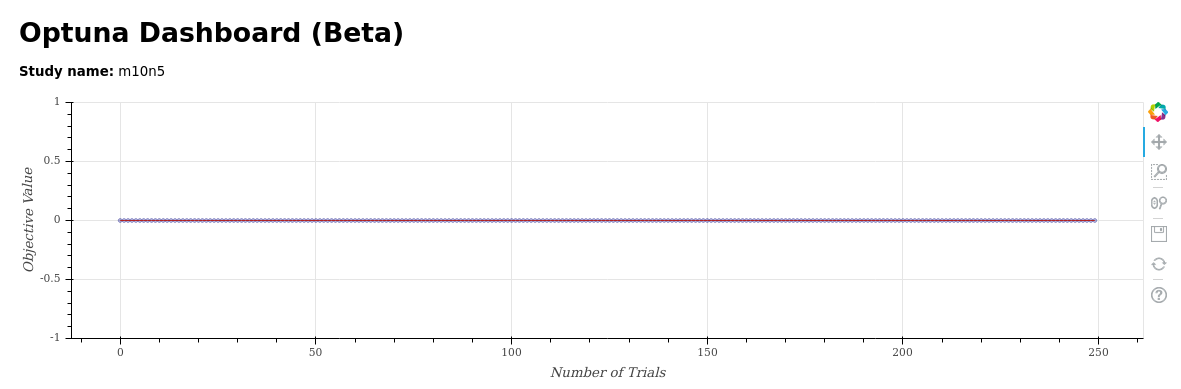
D-Wave DW-2000Q_6 実行結果
ほぼ同じコードを一世代前のチップでも実行しました。
こちらも結果は同じでした。問題期は小さいものの、実際に埋め込まれた結果を見ると、結構ビットを消費しており問題規模は小さいものの、なかなか難しいことがわかります。
| パラメータ探索結果 | 埋め込み結果 |
|---|---|
 |
 |
まとめ
あたらしいチップAdvantageもでて、面白くなってきたD-Waveですが現状では少し難しい問題が解けるという状況にありません。
特に、線形計画として解けるような問題は、従来手法に手も足も出ない感じです。
実際のプロジェクトなどではここからさらに工夫をこらして、D-Waveの特性を生かせるか見ていくのですが、本記事では時間の都合もありここまで。
※さすがにおかしい気がするので、バグを見つけた方は教えてください。
評価に用いたコードは以下