Go to Qiita Advent Calendar 2024 Top
LoginSignup
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@__Kat__in株式会社Enginee

ScannのAnisotropic Vector Quantizationを実装してみる

Last updated at Posted at 2024-09-02

株式会社Engineeの@__Kat__です。
RAG案件など、Vector Searchを触ることも増えてきたので今更ながら入門しscannについてまとめてみました。

TL;DR

  • scannの公式実装がよくわからかったため手を動かしてみる。
  • scannライブラリ全体の実装を追うのは限界があったため論文中のAnisotropic Vector Quantizationを実装した

はじめに

NNの発展によって複雑な情報を数百次元程度の密なベクトルで高精度な表現を獲得することが可能となっています。特にLLMの発展により多様なデータのベクトル表現を得ることが可能となり、いわゆるRAGや、レコメンドなどで活発に利用されています。

ベクトル検索は、クエリベクトルに対して類似度が高いベクトルを返すことで実現します。これらはk-NNという手法として昔から有名ですが、データ数が多いと時間がかかりすぎます。そのため近似的な計算を行うApproximate-NN(ANN)と呼ばれる手法があります。

ANNのアルゴリズムは多く存在しますが、今回はその中でも2020年にGoogleが発表したScann1と呼ばれるアルゴリズムを見ていきます。ScannはVertex AI Mathcing Engineの内部で利用されており、大規模で低レイテンシーなベクトル検索を提供しています。

Scann

現在Googleが提供しているベクトル検索のコア部分のアルゴリズムがScannですが、このときよく参照される論文にはScannという言葉は出てこらず、内部で使用されているAnisotropic Vector Quantizationを提案したものだと思われます。ScannはOSSとしても公開されているのですが、論文を読んだだけでは理解ができません。実際のところ、この実装は論文に記載があるように以前のGoogleによる2本の論文に近いです。

ちなみにOSSの実装では最近新たに提案されたSOARも実装されています。

Scannの論文の新規性は、内積を尺度としたときのベクトル量子化における新たな損失関数の提案です。

ベクトル量子化

ベクトル量子化とはベクトルを一つの離散値に割り当てる(量子化)する技術であり、k-meansなどを利用してベクトル→クラスタのインデックスへとマッピングすることで実現可能です。データをただ一点に割り当てるのでデータ効率は非常にいいですが精度は大きく落ちます。この量子化される代表点の集合をcodebookと呼びます。

image.png

直積量子化

直積量子化(Product Quantization, PQ)は[Jégou,2011]で提案された手法です。ANNのなかでよく見られるアプローチの一つで、ベクトル量子化をベースに高い保持効率を保ちつつ高い精度を出すことができます。

細かい資料は松井先生の資料2やサーベイ3を見ていただきたいのですが、具体的には、もとのD次元のベクトルをM個に分割し、その$D/M$個のベクトル空間それぞれに対してベクトル量子化を行います。
これにより、もとのfloat * Dのベクトルから $int * (D/M)$へとデータを変換します。

  1. (学習時) 学習データから各subspaceごとにcodebookを求める
  2. (検索時) クエリをもまた$M$個に分割してそれぞれでクラスタを計算
  3. クエリ$x$と検索データ$y$との距離 $\sum_{m=1}^M d(q(x^{(m)}),q(y^{(y)}))$を計算

ここで$q(x^{(m)})$は量子化を表し、kmeansでいえば近傍の重心$\hat{x}^{(m)}$に対して
$$q(x^{(m)})=\hat{x}^{(m)}$$
です。また、$d(q(x^{(m)}),q(y^{(y)}))$は実際には
$$\hat{d}(x^{(m)},y^{(y)})=d(x^{(m)},q(y^{(y)}))$$と行われます。(Asymmetric Distance Computing)

image.png

Anisotropic Vector Quantization

直積量子化はANNで広く使われていましたが、このときの類似度は基本的にユークリッド距離を基準に計算されていました。単語の分散表現などでは例えば内積やコサイン類似度が使われることも多く、Googleの研究チームは内積を類似度として使用するときにユークリッド距離がベクトル量子化では不都合な状況であることを指摘しました。

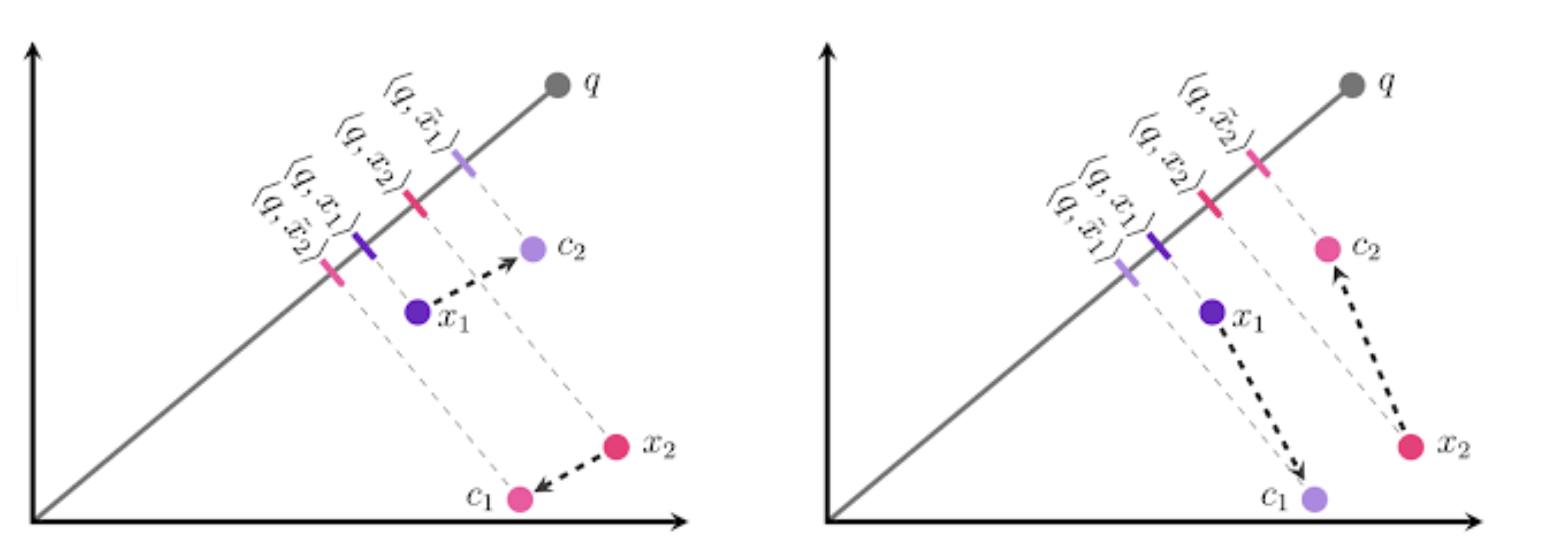
下側の画像の左側では、点$x_1$は最も近いクラスタ重心である$c_2$に、点$x_2$は$c_2$に量子化されていますが、元の内積と量子化後の内積の差が小さくなるためには、右図のように$x_1$は$c_1$へと量子化すべきです。
$$
min_c|q^Tx_1 - q^Tc| = c_2
$$

これを実現するために、内積の値に応じて$loss$の値に重み付けした損失関数を考えます。

$$
l(x,\hat{x},w) = \mathbb{E}_{q \sim Q}[w(q^Tx)(q^T(x-\hat{x}))^2]
$$

ここでQが単位超球面に一様分布しているとみなすと損失は以下のように分解でき、

$$
l(x,\hat{x},w) = h_{\parallel}(w,||x||)||r_{\parallel}(x,\hat{x})||^2 + h_{\perp}(w,||x||)||r_{\perp}(x,\hat{x})||^2
$$

$where,$

$$
h_{\parallel}(w,||x||) = (d - 1) \int_{0}^{\pi} w(||x|| \cos \theta) (\sin^{d-2} \theta - \sin^d \theta) d\theta
$$

$$
h_{\perp}(w,||x||) = \int_{0}^{\pi} w(||x|| \cos \theta)\sin^d \theta d\theta
$$

ただ、$w(t) = I(t > T)$とすることで

$$
l(x,\hat{x},w) \propto \eta(w,||x||)||r_{\parallel}(x,\hat{x})||^2 + r_{\perp}(x,\hat{x})||^2
$$

ここで$\eta= \frac{h_{\parallel}}{h_{\perp}}$であるが、$\eta$は以下の関係式が示されているのでこの式から簡単に計算できます

$$
\lim_{d \rightarrow \infty} \frac{\eta(w,||x||)}{d-1} = \frac{(T/||x||)^2}{1-(T/||x||)^2}
$$

アルゴリズム

Anisotropic Vector Quantizationのアルゴリズムは通常のベクトル量子化とほとんど同じで、

  1. 各ベクトルをAnistropic Lossが最も小さくなるcodebookに割り当てる
  2. codebookを次式に基づいて更新する

$$
c_j^* = \left( I\mathop{\rm \sum}\limits_{x_i \in X_j} h_{i,\perp} + \mathop{\rm \sum}\limits_{x_i \in X_j} \frac{h_{i,\parallel}-h_{i,\perp}}{||x||^2}x_ix_i^T \right )^{-1} \mathop{\rm \sum}\limits_{x_i \in X_j}h_{i,\parallel}x_i
$$

実装で困った点

ここまで見てきて、実装するにあたって２点問題点が浮上しました。

  1. 更新式に$h_{\parallel}$,$h_{\perp}$が出てくる(積分計算が必要となり解析的な解が求まらない)
  2. ベクトル量子化は行えるが、そのまま直積量子化に応用できそうにない(後述)

問題1に対する対処

$h_{\parallel}$,$h_{\perp}$の計算は複雑だが、これを以下のように$\eta$の問題に置き換える
($\eta$は極限値から簡単に計算できるため)

$$
c_j \leftarrow \mathop{\rm argmin}\limits_{c \in \mathrm{R
}^d} \mathop{\rm \sum}\limits_{x_i \in X_j} \eta(w,c) ||r_{\parallel}(x_i,\hat{x})||^2 + ||r_{\perp}(x_i,\hat{x_i})||^2
$$

これを論文Appendix 7.4に沿って解いていくと、

\begin{align}
l(x_i,c) &= \eta(w,||x_i||) ||r_{\parallel}(x_i,\hat{x})||^2 + ||r_{\perp}(x_i,\hat{x_i})||^2 \\ 
&= \eta(w,||x_i||) \left( ||x_i||^2 +  \frac{\hat{x}_i^Tx_ix_i^T\hat{x}_i}{||x_i||^2} - 2x_i^T\hat{x}_i\right) + ||x_i||^2 + ||\hat{x}_i||^2 - 2x_i^T\hat{x}_i - ||r_{\parallel}||^2 \\
&= (\eta(w,||x_i||)-1)\left( ||x_i||^2 +  \frac{\hat{x}_i^Tx_ix_i^T\hat{x}_i}{||x_i||^2} - 2x_i^T\hat{x}_i\right) + ||x_i||^2 + ||\hat{x}_i||^2 - 2x_i^T\hat{x}_i\\
&= \hat{x}_i^T\left(\frac{\eta(w,||x_i||)-1}{||x_i||^2} x_ix_i^T + I\right)\hat{x}_i - 2x_i^T\hat{x}_i + \eta(w,||x_i||)||x_i||^2\\
\end{align}

これは二次形式となり、クラスタに属するデータを足し合わせた場合、これが最小となる値は
$$
\left(\mathop{\rm \sum}\limits_{x_i \in X_j}\frac{\eta(w,||x_i||)-1}{||x_i||^2} x_ix_i^T + I\right)^{-1}\left(\mathop{\rm \sum}\limits_{x_i \in X_j}\eta(w,||x_i||)x_i\right)
$$

問題2に対する対処

通常の直積量子化では各subspace毎にベクトル量子化を行うことができるのですが、Anisotropic Lossではあるsubspaceのベクトル量子化で$r$を計算するために他のsubspaceでのcodebookが必要となります。
つまり一点に対してすべてのsubspace、クラスターにおいてanistoropic lossを計算しようと思うと $m^k$($m$はsubspaceの数、$k$はk-meansクラスターの数を)通りのlossの最小の組み合わせを計算する必要がありそうです。論文のこのあたりに対する言及がありそうなのですがいまいち理解できませんでした。

そのため実際の実装ではランダムにコードブックを割り当てたあと、「各subspaceごとの最適化」を複数回行うことで対処しました。

実装

nanopqと公式例に従っています。

通常の直積量子化 
import numpy as np
from scipy.cluster.vq import kmeans2, vq


def dist_l2(q, x):
    return np.linalg.norm(q - x, ord=2, axis=1) ** 2


def dist_ip(q, x):
    return q @ x.T


metric_function_map = {"l2": dist_l2, "dot": dist_ip}


class PQ:

    def __init__(self, M, Ks=256, metric="l2", verbose=True):
        assert 0 < Ks <= 2**32
        assert metric in ["l2", "dot"]
        self.M, self.Ks, self.metric, self.verbose = M, Ks, metric, verbose
        self.code_dtype = (
            np.uint8 if Ks <= 2**8 else (np.uint16 if Ks <= 2**16 else np.uint32)
        )
        self.codewords = None
        self.Ds = None

        if verbose:
            print(
                f"M: {M}, Ks: {Ks}, metric : {self.code_dtype}, code_dtype: {metric}",
            )

    def __eq__(self, other):
        if isinstance(other, PQ):
            return (
                self.M,
                self.Ks,
                self.metric,
                self.verbose,
                self.code_dtype,
                self.Ds,
            ) == (
                other.M,
                other.Ks,
                other.metric,
                other.verbose,
                other.code_dtype,
                other.Ds,
            ) and np.array_equal(
                self.codewords, other.codewords,
            )
        else:
            return False

    def fit(self, vecs, iter=20, seed=123, minit="points"):
        """Given training vectors, run k-means for each sub-space and create
        codewords for each sub-space.

        This function should be run once first of all.

        Args:
            vecs (np.ndarray): Training vectors with shape=(N, D) and dtype=np.float32.
            iter (int): The number of iteration for k-means
            seed (int): The seed for random process
            minit (str): The method for initialization of centroids for k-means (either 'random', '++', 'points', 'matrix')

        Returns:
            object: self

        """
        assert vecs.dtype == np.float32
        assert vecs.ndim == 2
        N, D = vecs.shape
        assert self.Ks < N, "the number of training vector should be more than Ks"
        assert D % self.M == 0, "input dimension must be dividable by M"
        assert minit in ["random", "++", "points", "matrix"]
        self.Ds = int(D / self.M)

        np.random.seed(seed)
        if self.verbose:
            print(f"iter: {iter}, seed: {seed}")

        # [m][ks][ds]: m-th subspace, ks-the codeword, ds-th dim
        self.codewords = np.zeros((self.M, self.Ks, self.Ds), dtype=np.float32)
        for m in range(self.M):
            if self.verbose:
                print(f"Training the subspace: {m} / {self.M}")
            vecs_sub = vecs[:, m * self.Ds : (m + 1) * self.Ds]
            self.codewords[m], label = kmeans2(vecs_sub, self.Ks, iter=iter, minit=minit)


        return self

    def encode(self, vecs):
        """Encode input vectors into PQ-codes.

        Args:
            vecs (np.ndarray): Input vectors with shape=(N, D) and dtype=np.float32.

        Returns:
            np.ndarray: PQ codes with shape=(N, M) and dtype=self.code_dtype

        """
        assert vecs.dtype == np.float32
        assert vecs.ndim == 2
        N, D = vecs.shape
        assert self.Ds * self.M == D, "input dimension must be Ds * M"

        # codes[n][m] : code of n-th vec, m-th subspace
        codes = np.empty((N, self.M), dtype=self.code_dtype)
        for m in range(self.M):
            if self.verbose:
                print(f"Encoding the subspace: {m} / {self.M}")
            vecs_sub = vecs[:, m * self.Ds : (m + 1) * self.Ds]
            codes[:, m], _ = vq(vecs_sub, self.codewords[m])

        return codes

    def decode(self, codes):
        """Given PQ-codes, reconstruct original D-dimensional vectors
        approximately by fetching the codewords.

        Args:
            codes (np.ndarray): PQ-cdoes with shape=(N, M) and dtype=self.code_dtype.
                Each row is a PQ-code

        Returns:
            np.ndarray: Reconstructed vectors with shape=(N, D) and dtype=np.float32

        """
        assert codes.ndim == 2
        N, M = codes.shape
        assert M == self.M
        assert codes.dtype == self.code_dtype

        vecs = np.empty((N, self.Ds * self.M), dtype=np.float32)
        for m in range(self.M):
            vecs[:, m * self.Ds : (m + 1) * self.Ds] = self.codewords[m][codes[:, m], :]

        return vecs

    def dtable(self, query):
        """Compute a distance table for a query vector.
        The distances are computed by comparing each sub-vector of the query
        to the codewords for each sub-subspace.
        `dtable[m][ks]` contains the squared Euclidean distance between
        the `m`-th sub-vector of the query and the `ks`-th codeword
        for the `m`-th sub-space (`self.codewords[m][ks]`).

        Args:
            query (np.ndarray): Input vector with shape=(D, ) and dtype=np.float32

        Returns:
            nanopq.DistanceTable:
                Distance table. which contains
                dtable with shape=(M, Ks) and dtype=np.float32

        """
        assert query.dtype == np.float32
        assert query.ndim == 1, "input must be a single vector"
        (D,) = query.shape
        assert self.Ds * self.M == D, "input dimension must be Ds * M"

        # dtable[m] : distance between m-th subvec and m-th codewords (m-th subspace)
        # dtable[m][ks] : distance between m-th subvec and ks-th codeword of m-th codewords
        dtable = np.empty((self.M, self.Ks), dtype=np.float32)
        for m in range(self.M):
            query_sub = query[m * self.Ds : (m + 1) * self.Ds]
            dtable[m, :] = metric_function_map[self.metric](
                query_sub, self.codewords[m],
            )

            # In case of L2, the above line would be:
            # dtable[m, :] = np.linalg.norm(self.codewords[m] - query_sub, axis=1) ** 2

        return DistanceTable(dtable, metric=self.metric)


class DistanceTable:
    """Distance table from query to codewords.
    Given a query vector, a PQ/OPQ instance compute this DistanceTable class
    using :func:`PQ.dtable` or :func:`OPQ.dtable`.
    The Asymmetric Distance from query to each database codes can be computed
    by :func:`DistanceTable.adist`.

    Args:
        dtable (np.ndarray): Distance table with shape=(M, Ks) and dtype=np.float32
            computed by :func:`PQ.dtable` or :func:`OPQ.dtable`
        metric (str): metric type to calculate distance

    Attributes:
        dtable (np.ndarray): Distance table with shape=(M, Ks) and dtype=np.float32.
            Note that dtable[m][ks] contains the squared Euclidean distance between
            (1) m-th sub-vector of query and (2) ks-th codeword for m-th subspace.

    """

    def __init__(self, dtable, metric="l2"):
        assert dtable.ndim == 2
        assert dtable.dtype == np.float32
        assert metric in ["l2", "dot"]
        self.dtable = dtable
        self.metric = metric

    def adist(self, codes):
        """Given PQ-codes, compute Asymmetric Distances between the query (self.dtable)
        and the PQ-codes.

        Args:
            codes (np.ndarray): PQ codes with shape=(N, M) and
                dtype=pq.code_dtype where pq is a pq instance that creates the codes

        Returns:
            np.ndarray: Asymmetric Distances with shape=(N, ) and dtype=np.float32

        """

        assert codes.ndim == 2
        N, M = codes.shape
        assert self.dtable.shape[0] == M

        # Fetch distance values using codes.
        dists = np.sum(self.dtable[range(M), codes], axis=1)

        # The above line is equivalent to the followings:
        # dists = np.zeros((N, )).astype(np.float32)
        # for n in range(N):
        #     for m in range(M):
        #         dists[n] += self.dtable[m][codes[n][m]]

        return dists
Anisotropic Quantization 学習コード(速度を度外視して愚直に数式通り書きました) 

import numpy as np
from tqdm import tqdm


def dist_l2(q, x):
    return np.linalg.norm(q - x, ord=2, axis=1) ** 2


def dist_ip(q, x):
    return q @ x.T


metric_function_map = {"l2": dist_l2, "dot": dist_ip}

def _initialize_kmeans_plusplus(X:np.ndarray, n_clusters:int, random_state:int):
    n_samples, n_features = X.shape
    centers = np.empty((n_clusters, n_features), dtype=X.dtype)
    centers[0] = X[np.random.RandomState(random_state).randint(n_samples)]
    for i in range(1, n_clusters):
        print(i)
        dist = np.linalg.norm(X[:,None] - centers[:i],axis=2)
        dist = np.min(dist, axis=1) / (dist ** 2).sum(axis=1) if i > 1 else np.min(dist, axis=1)

        indices  = np.random.choice(n_samples, p=dist / dist.sum())
        centers[i] = X[indices]
    return centers

class APQ:
    """Pure python implementation of Product Quantization (PQ) [Jegou11]_.

    For the indexing phase of database vectors,
    a `D`-dim input vector is divided into `M` `D`/`M`-dim sub-vectors.
    Each sub-vector is quantized into a small integer via `Ks` codewords.
    For the querying phase, given a new `D`-dim query vector, the distance beween the query
    and the database PQ-codes are efficiently approximated via Asymmetric Distance.

    All vectors must be np.ndarray with np.float32

    .. [Jegou11] H. Jegou et al., "Product Quantization for Nearest Neighbor Search", IEEE TPAMI 2011

    Args:
        M (int): The number of sub-space
        Ks (int): The number of codewords for each subspace
            (typically 256, so that each sub-vector is quantized
            into 8 bits = 1 byte = uint8)
        metric (str): Type of metric used among vectors (either 'l2' or 'dot')
            Note that even for 'dot', kmeans and encoding are performed in the Euclidean space.
        verbose (bool): Verbose flag

    Attributes:
        M (int): The number of sub-space
        Ks (int): The number of codewords for each subspace
        metric (str): Type of metric used among vectors
        verbose (bool): Verbose flag
        code_dtype (object): dtype of PQ-code. Either np.uint{8, 16, 32}
        codewords (np.ndarray): shape=(M, Ks, Ds) with dtype=np.float32.
            codewords[m][ks] means ks-th codeword (Ds-dim) for m-th subspace
        Ds (int): The dim of each sub-vector, i.e., Ds=D/M

    """

    def __init__(self, M: int, Ks:int =256, metric: str="l2", anisotropic_threshold: float=0.2, verbose: bool=True):
        assert 0 < Ks <= 2**32
        assert metric in ["l2", "dot"]
        self.M, self.Ks, self.metric, self.verbose = M, Ks, metric, verbose
        self.code_dtype = (
            np.uint8 if Ks <= 2**8 else (np.uint16 if Ks <= 2**16 else np.uint32)
        )
        self.anisotropic_threshold = anisotropic_threshold
        self.codewords = None
        self.Ds = None

        if verbose:
            print(
                f"M: {M}, Ks: {Ks}, metric : {self.code_dtype}, code_dtype: {metric}",
            )


    def fit(self, vecs, iter=20, seed=123, minit="points"):
        """Given training vectors, run k-means for each sub-space and create
        codewords for each sub-space.

        This function should be run once first of all.

        Args:
            vecs (np.ndarray): Training vectors with shape=(N, D) and dtype=np.float32.
            iter (int): The number of iteration for k-means
            seed (int): The seed for random process
            minit (str): The method for initialization of centroids for k-means (either 'random', '++', 'points', 'matrix')

        Returns:
            object: self

        """
        assert vecs.dtype == np.float32
        assert vecs.ndim == 2
        N, D = vecs.shape
        assert self.Ks < N, "the number of training vector should be more than Ks"
        assert D % self.M == 0, "input dimension must be dividable by M"
        assert minit in ["random", "++", "points", "matrix"]
        self.Ds = int(D / self.M)

        np.random.seed(seed)
        if self.verbose:
            print(f"iter: {iter}, seed: {seed}")

        # [m][ks][ds]: m-th subspace, ks-the codeword, ds-th dim
        init_code_data = vecs[np.random.choice(len(vecs),self.Ks, replace=False)]
        self.codewords = np.zeros(self.Ks *  D)
        for m in range(self.M):
            self.codewords[m*self.Ds*self.Ks:(m+1)*self.Ds*self.Ks] = init_code_data[:,m * self.Ds:(m + 1) * self.Ds].flatten()

        all_assign_label = np.zeros((N,self.M),dtype=np.int32)
        for i in range(iter):

            A = np.zeros((self.Ks * D,self.Ks * D), dtype=np.float32)
            C = np.zeros(self.Ks * D, dtype=np.float32)

            for j,data in enumerate(tqdm(vecs)):
                B = np.zeros((D, D * self.Ks), dtype=np.int32)
                norm_squared = np.linalg.norm(data) ** 2
                eta = self.eta(data)
                quantized = np.zeros(D)


                for m in range(self.M):
                    ind = np.random.randint(0,self.Ks) if i ==0 else all_assign_label[i][m]
                    quantized[m*self.Ds: (m+1)*self.Ds] = self.codewords[m * self.Ds*self.Ks + ind * self.Ds : m * self.Ds*self.Ks + (ind+1) * self.Ds]

                assign_indices = np.zeros(self.M, dtype=np.int32)

                for it in range(3):
                    for m in range(self.M):
                        anisotropic_losses = []
                        for k in range(self.Ks):
                            quantized[m*self.Ds: (m+1)*self.Ds] = self.codewords[m * self.Ds*self.Ks + k * self.Ds : m * self.Ds*self.Ks + (k+1) * self.Ds]

                            loss = self.anisiotropic_loss(data, quantized, eta)
                            anisotropic_losses.append(loss)
                        sub_cluster_index = np.argmin(anisotropic_losses)
                        assign_indices[m] = sub_cluster_index
                        quantized[m*self.Ds: (m+1)*self.Ds] = self.codewords[m * self.Ds*self.Ks + sub_cluster_index * self.Ds : m * self.Ds*self.Ks + (sub_cluster_index+1) * self.Ds]

                for m in range(self.M):
                    ind = assign_indices[m]
                    B[m*self.Ds:(m+1)*self.Ds,m*self.Ds*self.Ks + ind*self.Ds:m*self.Ds*self.Ks + (ind+1)*self.Ds] = np.eye(self.Ds)

                all_assign_label[j,:] = assign_indices
                x = data[:, np.newaxis]
                A +=  B.T @ ((eta - 1) / norm_squared * x @ x.T + np.eye(D)) @ B
                C += eta * B.T @ data



            try:
                from scipy.linalg import cho_factor, cho_solve
                c0, low = cho_factor(A)  # O(K**3 D**3)
            except:
                eig_set = np.linalg.eig(A)[0]
                min_eign = eig_set.min()
                max_eign = eig_set.max()
                reg = 1e-3
                print(f"{min_eign=},{max_eign=},{reg=}")
                dim = A.shape[0]
                c0, low = cho_factor(A + reg * np.eye(dim))

            old_codewords = self.codewords.copy()
            self.codewords = cho_solve((c0, low), C).flatten()#np.linalg.inv(A) @ C
            if np.sum(old_codewords - self.codewords) <= 1e-5:
                break
            print(f"iter:{i}, diff:{np.linalg.norm(old_codewords - self.codewords)}")
        np.save("data/codewords.npy",self.codewords)
        return self


    def eta(self, data:np.ndarray):
        T2 = self.anisotropic_threshold ** 2

        norm_squared = np.linalg.norm(data) ** 2
        dim = data.shape[-1]
        return (dim-1) * (T2 / norm_squared) / (1 - T2 / norm_squared)

    def anisiotropic_loss(self, data:np.ndarray, quantized: np.ndarray, eta=None):
        if eta is None:
            eta = self.eta(data)

        r_parallel = np.dot(data - quantized, data) * data / (np.linalg.norm(data) ** 2)
        r_parallel_norm = np.linalg.norm(r_parallel) ** 2
        r_perp = (data - quantized) - r_parallel
        r_perp_norm = np.linalg.norm(r_perp) ** 2
        return eta * r_parallel_norm + r_perp_norm

    def encode(self, vecs):
        """Encode input vectors into PQ-codes.

        Args:
            vecs (np.ndarray): Input vectors with shape=(N, D) and dtype=np.float32.

        Returns:
            np.ndarray: PQ codes with shape=(N, M) and dtype=self.code_dtype

        """
        assert vecs.dtype == np.float32
        assert vecs.ndim == 2
        N, D = vecs.shape
        assert self.Ds * self.M == D, "input dimension must be Ds * M"
        quantized = np.zeros(D)

        codes = np.empty((N, self.M), dtype=np.uint8)
        for i,data in enumerate(tqdm(vecs)):
            eta = self.eta(data)
            for m in range(self.M):
                ind = np.random.randint(0,self.Ks)
                quantized[m*self.Ds: (m+1)*self.Ds] = self.codewords[m * self.Ds*self.Ks + ind * self.Ds : m * self.Ds*self.Ks + (ind+1) * self.Ds]

            assign_indices = np.zeros(self.M, dtype=np.int32)
            for m in range(self.M):
                anisotropic_losses = []
                for k in range(self.Ks):
                    quantized[m*self.Ds: (m+1)*self.Ds] = self.codewords[m * self.Ds*self.Ks + k * self.Ds : m * self.Ds*self.Ks + (k+1) * self.Ds]

                    loss= self.anisiotropic_loss(data, quantized, eta)
                    anisotropic_losses.append(loss)
                sub_cluster_index = np.argmin(anisotropic_losses)
                assign_indices[m] = sub_cluster_index
            codes[i,:] = assign_indices
        return codes

    def decode(self, codes):
        """Given PQ-codes, reconstruct original D-dimensional vectors
        approximately by fetching the codewords.

        Args:
            codes (np.ndarray): PQ-cdoes with shape=(N, M) and dtype=self.code_dtype.
                Each row is a PQ-code

        Returns:
            np.ndarray: Reconstructed vectors with shape=(N, D) and dtype=np.float32

        """
        assert codes.ndim == 2
        N, M = codes.shape
        assert M == self.M
        assert codes.dtype == self.code_dtype

        vecs = np.empty((N, self.Ds * self.M), dtype=np.float32)
        for m in range(self.M):
            vecs[:, m * self.Ds : (m + 1) * self.Ds] = self.codewords[m][codes[:, m], :]

        return vecs

    def dtable(self, query):
        """Compute a distance table for a query vector.
        The distances are computed by comparing each sub-vector of the query
        to the codewords for each sub-subspace.
        `dtable[m][ks]` contains the squared Euclidean distance between
        the `m`-th sub-vector of the query and the `ks`-th codeword
        for the `m`-th sub-space (`self.codewords[m][ks]`).

        Args:
            query (np.ndarray): Input vector with shape=(D, ) and dtype=np.float32

        Returns:
            nanopq.DistanceTable:
                Distance table. which contains
                dtable with shape=(M, Ks) and dtype=np.float32

        """
        assert query.dtype == np.float32
        assert query.ndim == 1, "input must be a single vector"
        (D,) = query.shape
        assert self.Ds * self.M == D, "input dimension must be Ds * M"

        # dtable[m] : distance between m-th subvec and m-th codewords (m-th subspace)
        # dtable[m][ks] : distance between m-th subvec and ks-th codeword of m-th codewords
        dtable = np.empty((self.M, self.Ks), dtype=np.float32)
        for m in range(self.M):
            query_sub = query[m * self.Ds : (m + 1) * self.Ds]
            codewords = self.codewords[m * self.Ds * self.Ks : (m + 1) * self.Ds * self.Ks].reshape(self.Ks,self.Ds)
            dtable[m, :] = metric_function_map[self.metric](
                query_sub, codewords,
            )

            # In case of L2, the above line would be:
            # dtable[m, :] = np.linalg.norm(self.codewords[m] - query_sub, axis=1) ** 2

        return DistanceTable(dtable, metric=self.metric)


class DistanceTable:
    """Distance table from query to codewords.
    Given a query vector, a PQ/OPQ instance compute this DistanceTable class
    using :func:`PQ.dtable` or :func:`OPQ.dtable`.
    The Asymmetric Distance from query to each database codes can be computed
    by :func:`DistanceTable.adist`.

    Args:
        dtable (np.ndarray): Distance table with shape=(M, Ks) and dtype=np.float32
            computed by :func:`PQ.dtable` or :func:`OPQ.dtable`
        metric (str): metric type to calculate distance

    Attributes:
        dtable (np.ndarray): Distance table with shape=(M, Ks) and dtype=np.float32.
            Note that dtable[m][ks] contains the squared Euclidean distance between
            (1) m-th sub-vector of query and (2) ks-th codeword for m-th subspace.

    """

    def __init__(self, dtable, metric="l2"):
        assert dtable.ndim == 2
        assert dtable.dtype == np.float32
        assert metric in ["l2", "dot"]
        self.dtable = dtable
        self.metric = metric

    def adist(self, codes):
        """Given PQ-codes, compute Asymmetric Distances between the query (self.dtable)
        and the PQ-codes.

        Args:
            codes (np.ndarray): PQ codes with shape=(N, M) and
                dtype=pq.code_dtype where pq is a pq instance that creates the codes

        Returns:
            np.ndarray: Asymmetric Distances with shape=(N, ) and dtype=np.float32

        """

        assert codes.ndim == 2
        N, M = codes.shape
        assert self.dtable.shape[0] == M

        # Fetch distance values using codes.
        dists = np.sum(self.dtable[range(M), codes], axis=1)

        # The above line is equivalent to the followings:
        # dists = np.zeros((N, )).astype(np.float32)
        # for n in range(N):
        #     for m in range(M):
        #         dists[n] += self.dtable[m][codes[n][m]]

        return dists

スクリプト

from pathlib import Path

import h5py
import numpy as np
from tqdm import trange

from scann_impl.apq import APQ
from scann_impl.pq import PQ


def compute_recall(neighbors: np.ndarray, true_neighbors: np.ndarray) -> float:
    total = 0
    for gt_row, row in zip(true_neighbors, neighbors):
        total += np.intersect1d(gt_row, row).shape[0]
    return total / true_neighbors.size


# with tempfile.TemporaryDirectory() as tmp:
#    response = requests.get("http://ann-benchmarks.com/glove-100-angular.hdf5")
#    loc = os.path.join(tmp, "glove.hdf5")
#    with open(loc, "wb") as f:
#        f.write(response.content)

glove_h5py = h5py.File(Path(__file__).parents[2] / "data" / "glove.hdf5", "r")

rng = np.random.default_rng(seed=1234)

dataset = glove_h5py["train"]
training_sample_size = 10000
training_dataset = dataset[()][rng.choice(len(dataset), training_sample_size, replace=False)]
training_dataset = training_dataset / np.linalg.norm(training_dataset, axis=1)[:, np.newaxis]

queries = glove_h5py["test"][()]

true_neighbors = glove_h5py["neighbors"][()]
# Instantiate with M=8 sub-spaces
for vq_class in [PQ,APQ]:
    pq = vq_class(M=25,Ks=16,metric="dot")

    # Train codewords
    pq.fit(training_dataset,iter=15)

    # Encode to PQ-codes
    X_code = pq.encode(dataset)  # (10000, 8) with dtype=np.uint8

    # Results: create a distance table online, and compute Asymmetric Distance to each PQ-code
    neighbors = np.empty((len(true_neighbors),100), dtype=np.int64)
    reordered_neighbors = np.empty((len(true_neighbors),100), dtype=np.int64)
    for i in trange(len(queries)):
        dists = pq.dtable(queries[i]).adist(X_code)  # (10000, )
        closest_indices = np.argsort(dists)[::-1][:2000]
        neighbors[i,:] = closest_indices[:100]
        sorted_indices = np.sort(closest_indices)
        # reordering
        reordered_neighbors[i,:] = sorted_indices[np.argsort((queries[i] * dataset[sorted_indices]).sum(axis=1))[::-1][:100]]

    # we are given top 100 neighbors in the ground truth, so select top 10
    print(f"Recall of {vq_class.__name__}(no reorder): {compute_recall(neighbors, true_neighbors[:, :10])}")
    print(f"Recall of {vq_class.__name__}(reorder): {compute_recall(reordered_neighbors, true_neighbors[:, :10])}")

結果

  • 手法
    • PQ: 通常の直積量子化
    • APQ: Scann
  • rescore
    • 最終的に得られた近似解を厳密に再計算して並び替える
> Recall of PQ(no rescore): 0.5848
> Recall of PQ(rescore): 0.6256

> Recall of APQ(no rescore): 0.37489
> Recall of APQ(rescore): 0.69028

となり、rescoreしたときは通常のPQを上回るRecallを確認できました。

実際にpythonからscannライブラリを使って実装したときも最後のreorderの有無でスコアが大きく変わりました。
image.png

最後に

興味が有る方ご連絡お待ちしております。カジュアル面談も歓迎です。

  1. Accelerating Large-Scale Inference with Anisotropic Vector Quantization
    Announcing ScaNN: Efficient Vector Similarity Search ↩

  2. 近似最近傍探索の最前線
    近似最近傍探索とVector DBの理論的背景 ↩

  3. A Survey of Product Quantization ↩

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?