前回:基礎から分かる時系列分析 2.カルマンフィルタ (数理的な導出)
3.1モデルの定義
ローカルレベルモデルとは、次のようなランダムウォークを表す状態空間モデルのこと。遷移行列が単位行列。
\begin{cases}
{\bf x}_t&={\bf x}_{t-1}+{\bf x}_t\ \ \ \ {\bf w}_t\sim\mathcal{N}({\bf 0},W)\\
{\bf y}_t&={\bf x}_t+{\bf v}_t\ \ \ \ \ {\bf v}_t\sim\mathcal{N}({\bf 0},V)
\end{cases}
# ---
# モデルの定義
# ---
mod = dlmModPoly(order = 1)
dlmライブラリのdlmModPoly()関数でモデルを定義した。この関数は多項式モデルを設定するもので、order=1とすることで次数1の多項式モデル(ローカルレベルモデル)となる。他にもシステムノイズや観測ノイズ、事前分布も設定できる。システムノイズと観測ノイズはモデルのパラメータであるから、
3.2 パラメータの特定
システムノイズと観測ノイズを最尤推定する。
# ---
# パラメータの特定
# ---
build_dlm = function(par){
# モデルのパラメータを設定する関数
mod$W[1,1] = exp(par[1]) # 負の領域を探索しないよう指数変換を行う
mod$V[1,1] = exp(par[2])
return(mod)
}
fit_dlm = dlmMLE(y = Nile, parm = c(0,0), build = build_dlm)
mod = build_dlm(fit_dlm$par)
モデルを定義、構築する関数build_dlmを作り、dlmMLEでパラメータの最尤推定値を探索させ、推定結果をもとにモデルを構築している。fit_dlm$parが返す値は指数変換前の値なのでそのまま代入して良い。
3.3 フィルタリング
フィルタリングを実施する。
# ---
# フィルタリングの実施
# ---
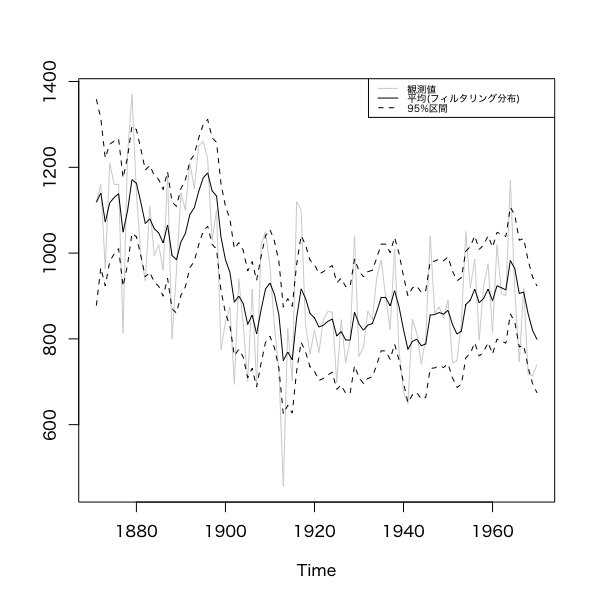
dlmFiltered_obj = dlmFilter(y = Nile, mod = mod)
# フィルタ分布の平均、標準偏差の導出
m = dropFirst(dlmFiltered_obj$m) # 先頭の事前分布の平均をドロップ
m_sdev = sqrt(
dropFirst( # 先頭を事前分布の分散をドロップ
as.numeric(
dlmSvd2var(dlmFiltered_obj$U.C, dlmFiltered_obj$D.C) # 特異値を分散に戻す
))
)
m_quant = list(m + qnorm(0.025, sd = m_sdev), m + qnorm(0.975, sd = m_sdev)) # 95%信頼区間
# 結果のプロット
oldpar = par(no.readonly = T)
par(family = "HiraginoSans-W4")
ts.plot(cbind(Nile, m, do.call('cbind', m_quant)),
col = c('lightgray', 'black', 'black', 'black'),
lty = c('solid', 'solid', 'dashed', 'dashed'))
legend(legend = c('観測値', '平均(フィルタリング分布)', '95%区間'),
lty = c('solid', 'solid', 'dashed', 'dashed'),
col = c('lightgray', 'black', 'black', 'black'),
x = 'topright', text.width = 32, cex = 0.6)
par(oldpar)
dlmFilter()関数でフィルタリングを行う。この関数は観測値yとモデルmodの他に
- m:フィルタ分布の平均
- U.C.,D.C.:フィルタ分布の共分散行列の特異値分解。dlmSvd2varで共分散行列に戻る。
などを返す。
3.4予測
10期先までの予測を行う。
# ---
# 予測
# ---
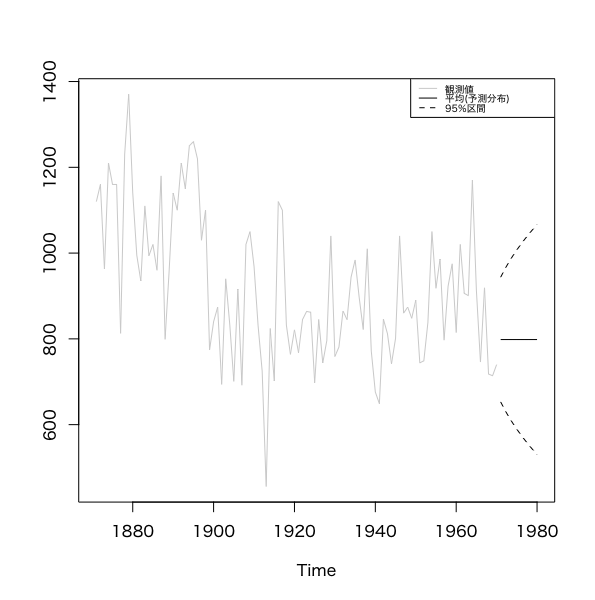
dlmForecasted_obj = dlmForecast(mod = dlmFiltered_obj, nAhead = 10)
# 予測分布の平均、標準偏差の導出
a = ts(data = dlmForecasted_obj$a, start = c(1971,1))
a_sdev = sqrt( as.numeric( dlmForecasted_obj$R ) )
a_quant = list(a + qnorm(0.025, sd = a_sdev), a + qnorm(0.975, sd = a_sdev))
# 結果のプロット
oldpar = par(no.readonly = T)
par(family = "HiraginoSans-W4")
ts.plot(cbind(Nile, a, do.call('cbind', a_quant)),
col = c('lightgray', 'black', 'black', 'black'),
lty = c('solid', 'solid', 'dashed', 'dashed'))
legend(legend = c('観測値', '平均(予測分布)', '95%区間'),
lty = c('solid', 'solid', 'dashed', 'dashed'),
col = c('lightgray', 'black', 'black', 'black'),
x = 'topright', text.width = 26, cex = 0.6)
par(oldpar)
dlmForecast()関数で予測を行う。この関数は
- a:予測分布の平均ベクトル
- R:予測分布の共分散行列
などを返す。