宇宙人はどこにいるのか？ドレイクの方程式とpythonを使って計算してみた。

#概要
ドレイクの方程式を使って銀河系にあるエイリアン文明について計算してみる

#環境
Mac
Jupyter Notebook
Python3

#ドレイクの公式

1961年に天文学者のドレイク先生が興味深い式を作りました。

N=R_{*}\times f_{p}\times n_{e}\times f_{l}\times f_{i}\times f_{c}\times L

この式に適切なパラメータを与えると我々とコンタクトをとりそうなエイリアン文明の数（銀河系内に限る）を求めることができるそうです。本当かな・・・

この式のパラメーターはウィキペディアによると以下の通りです。

名前	定義
$R_{*}$	人類がいる銀河系の中で1年間に誕生する星（恒星）の数
$f_{p}$	ひとつの恒星が惑星系を持つ割合（確率）
$n_{e}$	ひとつの恒星系が持つ、生命の存在が可能となる状態の惑星の平均数
$f_{i}$	発生した生命が知的なレベルまで進化する割合（確率）
$f_{c}$	知的なレベルになった生命体が星間通信を行う割合
$L$	知的生命体による技術文明が通信をする状態にある期間（技術文明の存続期間）

なんだか難しそうですが、ドレイク先生はこの式を作るにあたって次のようにパラメーターを設定しました。(ウィキペディアから引用)

$R_{*}=10$ 個/年 (銀河系の生涯を通じて、年平均10個の恒星が誕生する)
$f_{p}=0.5$ (あらゆる恒星のうち半数が惑星を持つ)
$n_{e}=2$ (惑星を持つ恒星は、生命が誕生可能な惑星を二つ持つ)
$f_{l}=1$ (生命が誕生可能な惑星では、100%生命が誕生する)
$f_{i}=0.01$ (生命が誕生した惑星の1%で知的文明が獲得される)
$f_{c}=0.01$ (知的文明を有する惑星の1%が通信可能となる)
$L=10,000$ 年 (通信可能な文明は1万年間存続する)

では、さっそくこの式とパラメーターをpythonに投入して銀河系にあるエイリアン文明の数を数えてみましょう。

import math

def culcDrakeEq(r, fp, ne, fl, fi, fc, l):
    return r * fp * ne * fl* fi * fc * l

#ドレイクが1961年に採用した値を使用
n = culcDrakeEq(10, 0.5, 2, 1, 0.01, 0.01, 10000)

print(n)

結果：10.0

銀河系にはエイリアン文明が10個あるということになりました。
なんか少ないですね。スタートレック（※SFシリーズ）とかだと毎週新しいエイリアンが出てくるのですが。
ちょっとパラメーターをいじってみましょう。

#銀河系ができてから今までに存在したエイリアン文明の数

パラメーターの最後の$L=10,000$ 年 (通信可能な文明は1万年間存続する)ですが、これは１万年が経過した文明は滅びるものとしてカウントしないということです。では、「現在の銀河系に存在しているエイリアン文明の数」、ではなくて、「銀河系ができてから今までに存在したエイリアン文明の数」を数えるにはどうしたら良いでしょうか。
銀河系はおよそ100億年前に今の形になったとされています。できた当初から多くの星が存在していたそうなので、パラメーターのその他の条件は変わらないとして、$L=100億年$を入力すれば良さそうです。

#銀河系ができてから今までに存在したエイリアン文明の数
n = culcDrakeEq(10, 0.5, 2, 1, 0.01, 0.01, 10000000000)

結果：10000000.0

銀河系には今までに１千万のエイリアン文明が存在していたことになりました。
なかなかすごい数です。いつか人類は宇宙探索の果てに、枯れた惑星にかつてのエイリアンたちの繁栄の後を見出すかもしれません。

#エイリアン文明の位置を図で表してみる

では、話を元に戻すとして、現存するエイリアン文明は地球からどのくらい離れたところにいるのでしょうか。図で表してみたいと思います。
単純にするため以下を仮定します。

• 銀河系は渦巻状ですが、正円に近似するとします
• 銀河系のどの場所でも星が生まれる確率は均一とします

import math
import random as rnd
import numpy as np
# matplotlib をインラインで使用することを指定する
%matplotlib inline
# ライブラリの読み込み
import matplotlib.pyplot as plt
from matplotlib.ticker import ScalarFormatter

#グラフのサイズ調整
fig = plt.figure(figsize=(8.0, 8.0))
fig.add_subplot()

#銀河系に見立てた半径五万(光年)の円を描画する
r = 50000
#円の方程式を使う
x = np.arange(-r, r)
yp = np.sqrt(r**2 - x**2)
ym =  - np.sqrt(r**2 - x**2)
#プロットする
plt.plot(x,yp)
plt.plot(x,ym)

#地球をプロットする(極座標を使用する)
#銀河系中心から地球までの距離25800(光年)
earthr = 25800
#偏角は何でも良いがここでは−1ラジアンとする
#x座標
earthx = earthr * math.cos(-1)
#y座標
earthy = earthr * math.sin(-1)
#プロットする
plt.plot(earthx,earthy, marker='o', mec='b', mew=4, linestyle='None')
#地球と分かるようにラベルする
plt.annotate('Earth', xy=(earthx-2000,earthy+2000))

for num in range(10):

    #ランダムに点をプロットする
    #銀河系中心からの距離(点が均一になるよう密度を調節する)
    rndr = r * np.sqrt(rnd.random())
    #偏角をランダムにとる
    rndtheta = rnd.uniform(-math.pi, math.pi) 
    #x座標
    rndx = rndr * math.cos(rndtheta)
    #y座標
    rndy = rndr * math.sin(rndtheta)
    #プロットする
    plt.plot(rndx,rndy, marker='o', mec='r', linestyle='None')
    #地球までの距離をピタゴラスの定理を用いて算出する
    rndn = round(np.sqrt(np.abs(earthx-rndx)**2 + np.abs(earthy-rndy)**2))
    #距離をラベルする
    plt.annotate(rndn, xy=(rndx-2000,rndy+2000))

#描画する    
plt.show()
    

結果の図です。

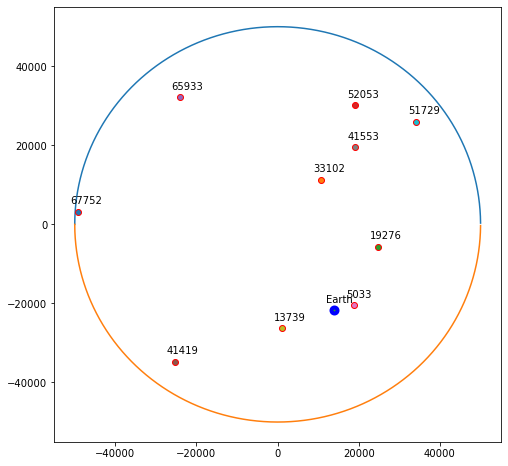
円が銀河系、円の中の右下の青い点「Earth」が地球です。そのほかの点はエイリアン文明、点の上の数字は地球からの距離(光年)です。
ランダムに１０個エイリアン文明をプロットしてみると、銀河系の端の遠いところにも出現しますが、地球の近く、5033光年の距離のところにもエイリアン文明が出現しました。
これは、地球から強力な電波を出して交信を試みれば、5033年後にはエイリアン文明に気づいてもらえる、ということでしょうか。
ただし、5033年が経過するよりも前にエイリアン文明が滅んでしまった場合、我々の電波をキャッチできなくなります。
一方、エイリアン文明は毎年新しく生まれる可能性があるので、もしかしたら、電波発信中にもっと地球の近くに生まれたエイリアン文明が、電波をキャッチしてくれるかもしれません。

#電波を出し続ければ何年くらいでエイリアンに気づいてもらえるのか

では、今から全方位に強力な電波を発射し続けたとして、何年くらいでエイリアンに気づいてもらえるのか、シュミレーションしてみましょう。

シュミレーションにあたって次を仮定します。

• 銀河系には1万年前からエイリアン文明が存在しているとする
• 銀河系に誕生するエイリアン文明はランダムに分布するとする
• 1万年を過ぎたエイリアン文明は滅びる
• 地球文明は電波がエイリアン文明に到達するまで滅びずに電波を出し続けるとする
• ある任意の年に新しいエイリアン文明が誕生する確率はドレイクの公式に$L=1年$を指定して得られる値とする

では、シュミレーションを1万回繰り返して、エイリアンに電波がキャッチされるのに要する年数の分布を見てみましょう。

import math
import random as rnd
import numpy as np
# matplotlib をインラインで使用することを指定する
%matplotlib inline
# ライブラリの読み込み
import matplotlib.pyplot as plt
from matplotlib.ticker import ScalarFormatter

#グラフのサイズ調整
fig = plt.figure(figsize=(16.0, 8.0))
fig.add_subplot()

#銀河系の半径
r = 50000
#銀河系中心から地球までの距離
earthr = 25800
earthx = earthr * math.cos(-1)
earthy = earthr * math.sin(-1)

#ドレイクの公式の関数
def culcDrakeEq(r, fp, ne, fl, fi, fc, l):
    return r * fp * ne * fl* fi * fc * l

#銀河系で1年にエイリアン文明が生まれる確率
posiblity = culcDrakeEq(10, 0.5, 2, 1, 0.01, 0.01, 1)

#生まれたエイリアン文明から地球までの距離を算出する関数
def culcNewAlienCivDist(r):

    #銀河系の中にランダムにエイリアン文明をプロットする
    rndr = r * np.sqrt(rnd.random())
    rndtheta = rnd.uniform(-math.pi, math.pi) 
    rndx = rndr * math.cos(rndtheta)
    rndy = rndr * math.sin(rndtheta)
    #ピタゴラスの定理を用いて地球からエイリアン文明までの距離を算出する
    distance = np.sqrt(np.abs(earthx-rndx)**2 + np.abs(earthy-rndy)**2)

    return distance 

#エイリアン文明に電波が届くまでに要した年数を求める関数
def culcIntercYear(posiblity):

    allAlienDist = dict()
    #1万年前から存在していたエイリアン文明を配列に入れておく
    for year in range(10000):
        if rnd.randrange(1,1/posiblity) == 1:
            allAlienDist[year] = culcNewAlienCivDist(r)  

    #地球を発した電波の進んだ距離(光年)
    lightd = 0
    past = 0
    #地球を発した電波が銀河系の端まで進むまでの年月ループする
    for year in range(r*2-(r-earthr)):

        for key in list(allAlienDist):
            if key <= past:
                #１万年を過ぎたエイリアン文明は消す
                allAlienDist.pop(key)

        #新しいエイリアン文明が生まれる確率
        if rnd.randrange(1,1/posiblity) == 1:
            #新しいエイリアン文明を追加する
            allAlienDist[year] = culcNewAlienCivDist(r)

        if len(allAlienDist) > 0:
            #エイリアン文明から地球までの距離 <= 地球を発した電波の進んだ距離
            if min (allAlienDist.values()) <= lightd:
                #エイリアン文明に電波が届くまでに要した年数
                intercYear = year
                break

        #電波の進んだ距離に１光年分の距離を足す
        lightd = lightd + 1  
        past = past + 1

    return intercYear
 
bins = list()
intercYearRange = list()
intercYearCntList = list()
yearGroup = 100
intercYearRange.append(0)
intercYearCntList.append(0)
#分類用リスト作成
while  yearGroup < r*2-(r-earthr):   
    bins.append(yearGroup)
    intercYearRange.append(yearGroup)
    intercYearCntList.append(0)
    yearGroup = yearGroup + 100

#シュミレーションを一万回繰り替えす
for num in range(10000):
    
    #エイリアン文明に電波が届くまでに要した年数を求め百年単位に分類する
    inds = np.digitize(culcIntercYear(posiblity), bins)
    intercYearCntList[inds] = intercYearCntList[inds] + 1 

#グラフをプロットする    
plt.plot(intercYearRange,intercYearCntList)
plt.show()

1万回シュミレーションをした結果のグラフです。横軸がエイリアン文明に電波が届くまでに要した年数、縦軸が1万回のうちその年数を要した回数です。

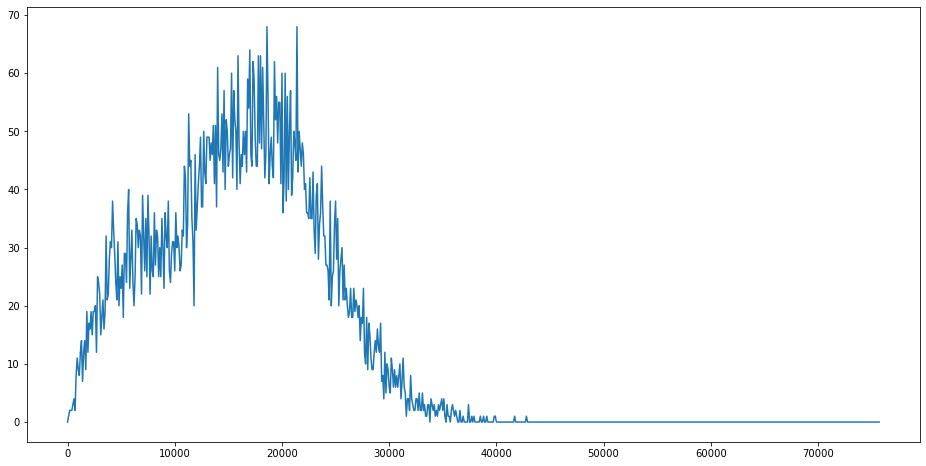
結果をみてみると、18000年あたりにピークがあるように見えます。エイリアンとの交信を試みた場合、18000年後にようやくエイリアン文明に届く可能性が高いようです。
これは地球文明が長く繁栄することを祈るしかないようですね。

#まとめ
これまでの結果を見ると、どうやらエイリアンとのファーストコンタクトはまだまだ先のようです。ですが、これはあくまで確率の話です。もしかしたら、地球近傍の恒星系に発達したエイリアン文明があって、日々こちらを観察しているのかもしれません。
そのほうが夢がありますね。

では、また次回〜
長寿と繁栄を〜