使えると便利だけど口頭で説明するとめんどくさいMathノードの解説記事を書きました。
アドベントカレンダー
- これは、NeosVRアドベントカレンダー13日目の記事です
説明の方法
- 文字とか図とかをつかいます。
- グラフの画像も載せます。
- TノードやElapsedTimeと組み合わせていい感じの動きを表現できるものもあるので、それ向けです。
何かと便利なやつ
Abs
入力
出力
説明
- 絶対値。Absは、絶対値を英訳であるAbsolute valueの頭文字。
- プラスの数字であればそのまま、マイナスの数字であればプラスにしたものを出力する。
- 入出力の例
| 入力 |
-2 |
-1 |
0 |
1 |
2 |
| 出力 |
2 |
1 |
0 |
1 |
2 |
グラフ
 |
| Googleで「abs(x)」と検索しても同じ形のグラフが出てくる。 |
使い方
- マイナスの数を入力したときに壊れたりするノードを使うときに、入力値にくっつけておくと安心
- Logや、Sqrtなどは、マイナスの数を入力するとNaN(Not a Number、数字でない)になります。
- この場合はAbsよりもMax(0,x)を使ったほうがいいかも。
注意
- ベクトルの絶対値(ノルム)をとりたい場合は、AbsではなくOperators->|V|を使ってください。
Avg
入力
- 数字その1 <float、double、およびそれらのベクトル>
- 数字その2 <float、double、およびそれらのベクトル>
- 数字その3以上(いくらでもふやせる) <float、double、およびそれらのベクトル>
出力
- 入力された数字の平均
- ここでの平均は、全部足し合わせて入力の個数で割ったものです。
説明
-
平均。Averageの略。
-
入力の平均の値を出力します。
- float2(x,yと表せる)や、float3(x,y,zと表せる)を入力した場合、x,y,zそれぞれの平均が出力されます
-
入出力例
 |
| float2のAvgは、XとYそれぞれの平均値が計算されている。 |
Clamp,Clamp01
入力
- 上限と下限を設定したい数字 <任意の数字、ベクトル>
- 下限の数字 (Clamp01の場合ない) <任意の数字、ベクトル>
- 上限の数字 (Clamp01の場合ない) <任意の数字、ベクトル>
出力
説明
- 入力に上限と下限を設定します。
- "Clamp01"は、入力が0以下なら0、0から1の間ならそのまま、1以上なら1を出力します。
- "Clamp"は、この上限と下限を好きに設定できるものです
入出力例(Clamp01)
| 入力 |
-1 |
-0.5 |
0 |
0.5 |
1 |
1.5 |
| 出力 |
0 |
0 |
0 |
0.5 |
1 |
1 |
グラフ
 |
| 0以下なら0、1以上なら1。その間のときはそのまま出力される。 |
使い方
 |
Clampの入力は、上から順番に「入力、下限、上限」。
画像は下限を-1に、上限を1に設定した例。 |
Floor, Floor to int
入力
- 好きな数字 <Float、Double及びそれらのベクトル>
出力
説明
- 床関数。切り捨てのこと。
- Floor to intは、出力がInt型のものです。
- 入力された数字より小さい整数のうち、一番大きい整数を出力します。
- ここで注意なのですが、「小数点以下をすべて0にした数字」ではありません。
- 例えば、-2.5を切り捨てた数字は-3.0になります。(-2.0ではない)
Ceil, Ceil to int
入力
- 好きな数字 <Float、Double及びそれらのベクトル>
出力
説明
- 切り上げ。
- Ceil to intは、出力がInt型のものです。
- 入力された数字より大きい整数の中で一番小さい整数を出力します。
Remap, Remap -1..1 to 0..1
入力
- 入力の最小値 (Remapのみ) <Float、Double>
- 入力の最大値 (Remapのみ) <Float、Double>
- 出力の最小値 (Remapのみ) <Float、Double>
- 出力の最大値 (Remapのみ) <Float、Double>
- 変換したい数字
出力
説明
- Remap -1..1 to 0..1は、-1から1までの入力を0から1に変換するノードです。
- ただのRemapは、入力と出力それぞれの上限と下限を指定して変換できます。
入出力例 (Remap -1..1 to 0..1)
| 入力 |
-1.0 |
-0.8 |
-0.6 |
-0.4 |
-0.2 |
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1.0 |
| 出力 |
0.0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1.0 |
補足
- 例えばRemap -1..1 to 0..1の中身は
- っぽいので、入力が-1から1でなくともいい感じに変換してくれます。
Ping Pong
入力
- 好きな数字 <任意の型の数字およびベクトル>
- 跳ね返りする幅 <任意の型の数字およびベクトル>
出力
説明
- ぴんぽん
- 好きな数字と、跳ね返りの幅(いずれもfloat)の二つの数字から計算します。
- 一つ目の値を0から大きくしていくと、二つ目の値で跳ね返って0でまた戻る…みたいな関数になります
グラフ
 |
| Elapsed Timeや、Tノードと組み合わせるとPannerのような動きが再現できます。 |
-
一つ目の数字がある程度大きい時に跳ね返りの幅の数字を変えてしまうと、めちゃくちゃな動きになります。
- これは、二つ目の数字を変えるとグラフの縮尺が変化したかのように振舞ってしまうからです。
-
図や文章だけで説明するのは大変なので、気になる人はこちらのサイトで動きを確認してください。
-
これと同じような問題はこれに限らず、Sin、Cosなどのあらゆる周期関数(繰り返しのある関数)で起こり得ます。
Repeat, Repeat01
入力
- 好きな数字 <任意の型の数字およびベクトル>
- 繰り返しの幅 <任意の型の数字およびベクトル>
出力
説明
- 好きな数字を0から大きくしていくと、繰り返しの幅で指定した数字以上にはならず、そこで繰り返すような動きになります。
Min
入力
- 入力その1 <任意の型の数字およびベクトル>
- 入力その2 <任意の型の数字およびベクトル>
- 入力その3以降 <任意の型の数字およびベクトル>
出力
説明
Max
入力
- 入力その1 <任意の型の数字およびベクトル>
- 入力その2 <任意の型の数字およびベクトル>
- 入力その3以降 <任意の型の数字およびベクトル>
出力
説明
- 入力された数字の中で最も大きい数字を出力します
- Max(X,0)のようにLogiXを組むと「Xが0以下のときは0で、そうじゃないときはそのまま数字を出力する」という振舞いになります。
Sign
入力
出力
説明
- 入力された数字が0より大きいとき1、0のとき0、0より小さいとき-1を出力します。
グラフ
 |
| 「符号を数字で判定できる」と考えられなくもないが、0のときは0であることを忘れてはならない。むしろその用途ならOperatorsの不等号ノード(<、>、≦、≧)を使うべき。 |
Round
入力
- 四捨五入したい数字 <任意の型の数字およびベクトル>
出力
- 四捨五入した結果 <任意の型の数字およびベクトル>
説明
Is Between
入力
- 判定したい数字 (数字)
- 上限 (数字)
- 下限 (数字)
出力
- 判定したい数字が上限と下限の間にいるかどうか (Boolean)
説明
- 判定したい数字が間にいるときTrue、そうでないときはFalseを出力します。
- 上限、あるいは下限と数字が同じ時もTrueになります。
三角関数
結局こいつは何者なのか
- 角度(単位はラジアン)に対する三角比を計算してくれる関数です。
-
こちらのリンクで三角関数の動きをわかりやすく説明しています。
 |
| こんなかんじです |
Sin
入力
- 角度(ラジアン) <Float、Doubleおよびそれらのベクトル>
出力
- 上の画像の黄色い三角形の、右の辺にあたる部分の長さを出力します。
Cos
入力
- 角度(ラジアン) <Float、Doubleおよびそれらのベクトル>
出力
- 上の画像の黄色い三角形の、下の辺にあたる部分の長さを出力します。
Tan
入力
- 角度(ラジアン) <Float、Doubleおよびそれらのベクトル>
出力
- 上の画像の紫の三角形の、右の辺にあたる部分の長さを出力します。
Asin, Acos(アークサイン、アークコサイン)
入力
- -1から1までの数字 <Float、Doubleおよびそれらのベクトル>
出力
- 入力された数字、関数に相当する-πからπまでの角度
説明
- sin、cosの逆関数です。Arc(弧)Sine、Arc Cosineの略。
Atan(アークタンジェント)
入力
- 任意の数字 <Float、Doubleおよびそれらのベクトル>
出力
- 入力された数字に対する角度を計算します。Tanの逆関数
Atan2
入力
- 角度を計算したい点のY座標
- 角度を計算したい点のX座標
出力
- 原点と(1,0)を結ぶ線分に対して、原点と(X,Y)を結ぶ線分のなす角度のうちπより小さい方を出力します。
数式
Sqrt
- 平方根。二乗してその数になる数。二乗根。
- 4だったら2、9だったら3。
- Sqrtは、Square Root(平方根)の略。
\sqrt{4} = 2
\\
\sqrt{9} = 3
Nth root
- N乗根。N乗してその数になる数。
- 4の2乗根(Sqrtと同じ)は2。27の3乗根は3。
Log, Log N, Log 10
- 「その数は底(てい)の数を何乗したものであるか」を出す。
- 8について2を底とした対数をとると、3である。
- なにもないLogの底の数字はe(ネイピア数)である。
- 迷ったらLog 10を使うとよい
Pow
入力
出力
説明
Sigmoid
入力
- すきな数字
- Sigmoid関数のゲイン(Neos内ではPowerと表記される)
出力
説明
- 入力された数字をSigmoid関数と呼ばれる関数に代入し、その結果を出力するもの。
- Sigmoid関数は数式で表すとこのようなものになります。
f(x,a)=\frac{1}{1+e^{-ax}}
\\
\\
\\e=2.71...
- eの-ax乗について、axはaとxを掛け合わせた数字であるためどっちにつないでも結果は変わりません。
- ただし、一般的にaは定数、変数はxに代入するものであるというのが常識です。
グラフ
 |
| 数学的には色々と利便性がある関数ではあるが、Neosに関しては0から1になめらかに遷移させるくらいしか使い道が無いし、それだったらCosLerpを使った方がなめらか。AIを作るくらいしか使い道がない。 |
Greatest Common Divisor
入力
- 数字A <Int,Longなどの整数値>
- 数字B <Int,Longなどの整数値>
出力
説明
- AとBを割り切れる自然数のなかで、一番大きいものを出力します。
Least Common Multiple
入力
- 数字A <Int,Longなどの整数値>
- 数字B <Int,Longなどの整数値>
出力
説明
- AとBの倍数に現れる共通の自然数のうち、最も小さい数字を出力します。
補完
Lerp,Multi Lerp
入力
- 一つ目の値 <任意の数字、ベクトル>
- 二つ目の値 <任意の数字、ベクトル>
- 三つ目以降の値(Multi Lerpのみ) <任意の数字、ベクトル>
- Lerpの度合い
出力
説明
- 補完する値が2つのときはLerpと表示されますが、+ボタンを押して3つ以上に増やすとMulti Lerpノードに変化します。
 |
| 勝手に変化する。どちらもノードメニューから直接取り出せる。 |
- Lerpノードの場合(Multi Lerpではない)入力された数字をそれぞれAとBとしたとき、Lerpの度合いを0から1に動かすと出力がAからBに直線的に変化します。
- Lerpの度合いが0以下の時はA、1以上の時はBになります。
- Multi Lerpノードの場合(Lerpではない)、0~1のときは1番目と2番目が、2~3のとき2番目と3番目が……というように補完されます。
 |
| 0と15までの補完を0.5だけ進めると7.5、20から40までの補完を0.5だけ進めると30。 |
グラフ
 |
| これをグラフで表すと |
 |
| このようになる |
Inverse Lerp
入力
- 補完元の数字 <任意の数字、ベクトル>
- 補完先の数字 <任意の数字、ベクトル>
- ある数字 <任意の数字、ベクトル>
出力
説明
- Lerpの逆関数です。
- 0から30までの補完で15が出たとき、Lerpの量は?という計算ができます。
Slerp, Multi Slerp
入力
- Rotationその1 <FloatQ>
- Rotationその2 <FloatQ>
- Rotationその3以降(Multi Slerpのみ) <FloatQ>
- Lerpの度合い <Float、要は数字>
出力
説明
Cosine Lerp, Multi Cosine Lerp
入力
- 一つ目の値 <任意の数字、ベクトル>
- 二つ目の値 <任意の数字、ベクトル>
- 三つ目以降の値(Multi Lerpのみ) <任意の数字、ベクトル>
- Lerpの度合い
出力
説明
- おおむねLerpと同じですが、補完の動きが直線ではなく余弦曲線(コサインカーブ)を描きます。
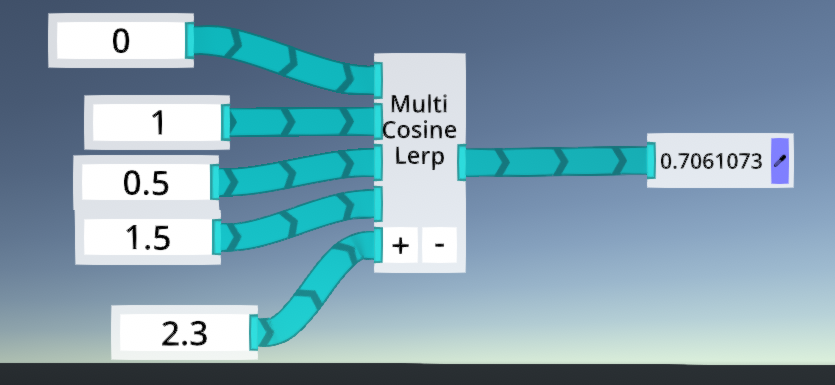 |
| 例えばこのような入力は |
 |
| これと同じものになります |
Cubic Lerp, Multi Cubic Lerp
入力
- 各点の大きさ
- 各点における傾き(正接,Tangent)
- Lerpの度合い
出力
説明
- おおむねCosine Lerpのようになめらかな補完をしますが、違いがあります。
- Cosine Lerpでは1,2,3……のように整数の部分では変化の速度(グラフの傾き)が0になりますが、CubicLerpではその傾きを制御できます。
- Tangentを全て0にするとCosine Lerpと同じ振舞になります。
要注意な補完系ノード
- これらのノードは、入力値に対して出力が一定ではなく、時間によって変化します。
Constant Lerp,Constant Slerp
入力
- 目標値 <Float、Double、およびそれらのベクトル>
- 変化速度[毎秒] <Float>
出力
説明
- 目標値に対して、一秒あたり変化速度で指定した数字ずつ出力値を変化させます。
Smooth Lerp
入力
- 目標値 <Float、Double、およびそれらのベクトル>
- 変化の速さ <Float>
出力
説明
- 1フレーム毎に、目標値との差分のうち時間当たりで一定割合ずつ近づくように変化します。
特殊
Δ(デルタ)
入力
出力
説明
- 入力された数字の、今のフレームと一つ前のフレームの時点での差分を出力するノードです
- 例えば、Transform -> Global TransformのPositionをこのノードにつなげ、出力をさらにOperators -> ÷dTにつなげると、GlobalTransformにつなげたSlotの、その瞬間におけるxyz各方向に対する速度が得られます。
Math > Constants(定数)について
- 言ってしまえばInputNodeと変わりません。
- 数学や、LogiXでよく使う数字がまとめてあります。
Deg -> Rad,Rad -> Deg
- 角度をラジアンに、ラジアンを角度に変換したいときの係数です。
- Deg -> Rad = 0.017453292....
- Rad -> Deg = 57.29577.....
 |
| 180°をラジアンに変換するとπラジアン、3.1415926……になる。 |
e
π,π/2,τ
- π(パイ)、円周率。
- π/2(にぶんのぱい)、円周率の半分。
- τ(たう)、2πのこと。
- τ = 6.283185……
- どうして2πではなくτなのか?を解説するとめっちゃ長くなるので、省略。
φ(ファイ)
\phi = \frac{1+\sqrt{5}}{2}=1.6180339...
おわりに
- LogiXに限らずどこでもつかえると思うのでぜひ活用してください。
- ミスがあれば連絡ください














