GANの性能評価に関する論文「Geometry Score: A Method For Comparing Generative Adversarial Networks」[1]に関して解説を行う.GANの評価指標としては,2016年にGANの提案者でもあるGoodefellowら[2]によって提案されたInception Scoreがあるが,それでは特定されなかったmode collapseを特定することもできている.
イントロダクション
GANでは,次の2点の問題がよく取り上げられる.
- 生成サンプルの質を異なるGAN同士でどうやって比較するのか.
- 同じ画像しか生成しなくなってしまうmode collapseをどうやって特定するのか.
KhrulkovとOseledetsはこの2つの問題を解消する手法としてGeometry Scoreを提案した.
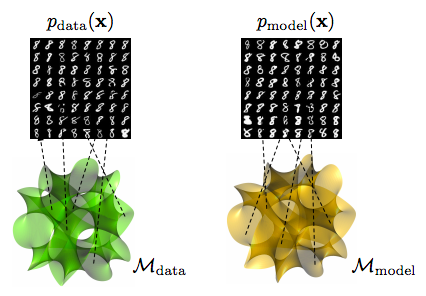
高次元空間のデータはより低次元空間の多様体へ射影できるであろうという多様体仮説[3]がベースにある.多様体とは,局所的にユークリッド空間とみなせる(すなわち,局所的にはユークリッド空間と同相である)位相空間のことであるが,もしもGANのGeneratorが生成モデルとして機能していれば,データセットが形成する多様体とGANの生成モデルが形成する多様体が呈す性質は似ていると考えられる.下の図は,データを多様体上の点と対応させているイメージ図である.
この考えに基づき,TDA(Topological Data Analysis, 位相的データ解析)の手法を用いているのがGeometry Scoreである.内容は,次のように展開する.
- 概要説明
- 単体複体
- アルゴリズム
- 実験結果の説明
概要説明
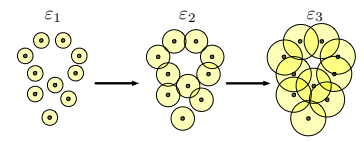
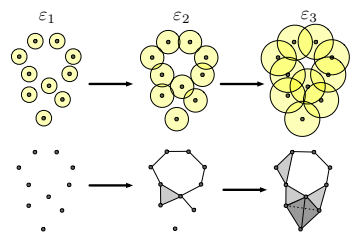
TDAでは,(抽象)単体複体の構成とそれらが形成する穴がポイントとなる.まず,データ点を中心とした円を考えていく(2次元だと円であるが,n次元ではn次元球である).
円の半径を大きくしていくと,穴が形成されているのがわかる.図では,半径$\varepsilon_1$では穴が形成されていないが,$\varepsilon_2$になると上側に穴が形成されている.さらに,$\varepsilon_3$より大きくなるとやがて穴が消えるのが直感的にわかるであろう.このように半径を時間とともに大きくしていったときの穴の出現・消滅に着目するのがTDAの基本的な発想である.これを単体複体という概念を用いて表すと次のようになる.
単体複体とは,集合同士が共通部分を有するかに着目した概念である.数学的な定義では,$k$次元単体は,$k+1$個の集合$B_0,\cdots,B_k$が共通部分を持つこと.すなわち,
$$
\bigcap_{i=0}^kB_i\neq\emptyset
$$
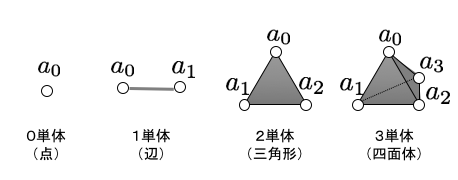
として定義される.0次元単体は点で表し,1次元単体は辺で表し,2次元単体は三角形を表す.
先ほどの図を改めて見比べてみよう.$\varepsilon_2$では円の集合同士が交わりを持ち,辺を構成していることがわかる.また,真ん中より左下側の3つの円が交わりを持ち,三角形を構成していることも見て取れる(三角形はこのように塗りつぶして表現する).
このようにして,データ周りの円を単体複体(特に円の集合の単体複体をチェック複体と呼ぶ)として考えたときの穴というトポロジカルな性質に基づいて,穴の相対的生存時間を考えていく.そのために,まずは単体複体,Witness複体を紹介し,それからアルゴリズムについて述べていく.
単体複体
ここでは,簡単に概念について説明していくが,数学的に詳しく知りたい人は平岡著の「タンパク質構造とトポロジー: パーシステントホモロジー群入門」[4],あるいは平岡作成のpdf[5]を参照にして欲しい.
$k$単体に関する定義はすでに述べたので,単体複体に関する定義から紹介する.$k$次元単体を$|a_0\cdots a_k|$と書く(ここで$a_i$は頂点である).単体$|a_0\cdots a_k|$の面であるとは,$k+1$個以下の頂点を用いた単体$|a_{i_0}\cdots a_{i_l}|,l\le k,i_n\in{1,\cdots,k}(n=0,\cdots,l)$である.例えば,2単体$|a_0a_1a_2|$の面は,$|a_0|,|a_1|,|a_2|,|a_0a_1|,|a_0a_2|,|a_1a_2|,|a_0a_1a_2|$である.
有限個の単体の集合$K$が単体複体であるとは,次の2つの条件を満たすことである.
- $\sigma\in K,\tau\subset\sigma\Rightarrow \tau\in K$.
- $\sigma,\tau\in K,\tau\cap\sigma\neq\emptyset\Rightarrow\tau\cap\sigma\subset\tau,\sigma$.
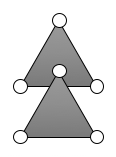
1つ目の条件は,$K$に属している単体の任意の面は$K$に属しているということである.2つ目の条件は,単体同士はきちんと張り合わせられているということである.例えば下のように状況は生じ得ないということである.
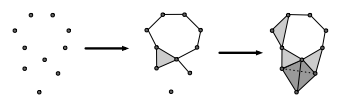
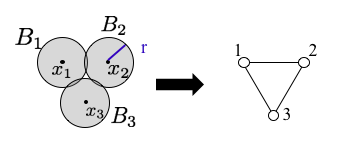
$n$次元球の集合$B_r(x_i)=\{x\in\mathbb{R}^n||x-x_i|\le r\}$に関する単体複体を考えたものがチェック複体である.例えば,左図のように3つの点を中心とした円を考えたとき,右図の単体複体が形成される.
今回は,このチェック複体を用いていきたいが,我々が対象としているGANでは,5,000点や60,000点といった大規模画像データを扱うことが多い.それだけ巨大な点の交わりを計算は,膨大な時間がかかる.2点間の交わりを計算するだけでも全組み合わせを考えれば,計算機爆発を起こすことは容易に想像がつくだろう.そこで,データ点のうち$L_0$個をサンプリングしたWitness複体を考える(サンプリングされた点をランドマーク点と呼ぶ).半径$\varepsilon$の単調増大列$\{\varepsilon_i\}$を考え,穴が誕生した時の時間と穴が消失した時間を計算する.
ここで,$k$次元の穴の定義を与える.$k$次元の穴とは,境界のない$k$次元図形で$k+1$次元図形の境界になっていないものである.例えば,1次元の穴は,境界のない1次元図形で,2次元図形の境界になっていないものである.上のチェック複体は,$|12|,|23|,|31|$という1単体を3つ有し,ループを形成している(すなわち,境界のない1次元図形である).また,$B_1,B_2,B_3$は共通部分を持たない($B_1\cap B_2\cap B_3=\emptyset$)ので,$|123|$はチェック複体に属さない(よって,2次元図形の境界とはなっていない).これから,先ほどのチェック複体は1次元の穴を1つ有していることがわかる(もしも$B_1\cap B_2\cap B_3\neq\emptyset$であれば,2次元図形の境界となっているので,1次元の穴とは考えない).
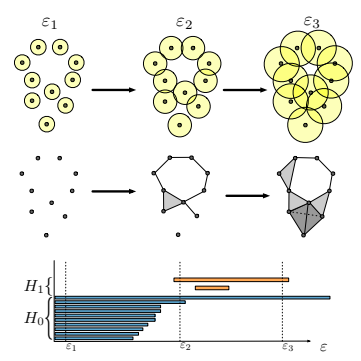
先ほどの図に戻ると,穴の生成と消滅は最下段の図のように表せる.
半径が大きくなり,集合2つが交わると,0次元の穴が消失していっている.また,$\varepsilon_2$で1次元の穴が1つ形成されている.下の方にある円も大きくしていくと1次元の穴を形成するが,すぐに消えていると考えられる.この穴の相対的生存時間の分布を考えていくことになる.この相対的生存時間の分布に関して,元のデータセットとGANが生成したモデルが似ていれば,良い画像を作り出していることになる(具体的にはL2誤差を取る).
アルゴリズム
パージステント・パラメータ$\alpha\in[0,\alpha_{max}]$とする.この時,$k$位ベッティ数は,
\beta_k(\alpha):=|\{[b_i,d_i]\in\{[b_i,d_i]\}_{i=1}^n:\alpha\in[b_i,d_i]\}
と定義する.ここで,$b_i,d_i$は$k$次元穴の誕生時間(birth time),消滅時間(death time)を表しており,$n$は生じた$k$次元穴の総数である.つまり,$k$位ベッティ数は,$k$次元穴が半径$\alpha$の時にどれぐらいありますか,っていうことを表している.このベッティ数を用いると,相対的生存時間(Relative Living Time)は,
RLT(i,k,X,L):=\frac{\mu(\{\alpha\in[0,\alpha_{max}]:\beta_k(\alpha)=i\})}{\alpha_{max}}
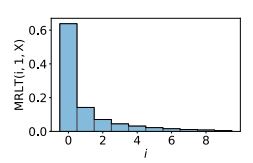
と定義される.RLTはその名の通り,$i$個の$k$次元穴は平均的に総時間$\alpha_{max}$に対してどれぐらい生存していましたか,ということを表している.$k$次元穴の数$i$に関して総和を取れば1になるのは自明であろう.
ここで,ランドマーク点はランダムに$X$からサンプリングすると述べた.しかし,1回のサンプリングでは当然モデルの位相的性質を表したとは言えない.そこで,何回もサンプリングを繰り返し,それらの平均を考える.すなわち,平均相対的生存時間(Mean Relative Living Time)を$L$に関する期待値として,
MRLT(i,k,X):=E_L[RLT(i,k,X,L)]
として定義する.今回は,1次元の穴だけ考えることにすれば,1次元の穴の個数別のMRLTの分布を比較すればよく,Geometry Scoreを次で定義する.
GS(X_1,X_2):=\sum_{i=0}^{i_{max}-1}(MRLT(i,1,X_1)-MRLT(i,1,X_2))^2
このGeometry Scoreによって,データセット間の位相的性質の近さがわかる.また,$\alpha_{max}$は,ランドマークの2点間の距離の最大値に比例$\alpha_{max}=\gamma d(L,L)$で決めると良い.ここで,比例定数$\gamma$は経験的に$1/128$ぐらいがうまくいくとわかっている(経験的に穴の個数の最大値は,$i_{max}=100$ぐらいが良い).よって,$N\times D$データセット$X$に関して,RLTは次のように計算すれば良い.
- データセット$X$,ランドマーク点のサンプル数$L_0$,比例定数$\gamma$,穴の個数の最大値$i_{max}$,サンプリング回数$n$,データ間の距離関数$dist$を入力として与える.
- Witness複体を計算する関数witness,パージステンス区間([誕生,消滅])を計算する関数persistenceを与える.
- $n$回次を繰り返す.
- ランドマーク点$L$をランダムに$X$から$L_0$個サンプリングする.
- $L,X$間の距離行列$d$を計算する.
- $\alpha_{max}=\gamma\max(dist(L,L))$を計算する.
- ウィットネス複体$W=witness(d,\alpha_{max},2)$を計算する.
- パージステンス区間$I=(W,1)$を計算する.
- 穴の数$i$に関して,それぞれ$RLT(i,1,X,L)$を計算する.
- MRLTを計算する.
- データセット間を比較する場合は,Geometry Scoreを計算する.
実験結果
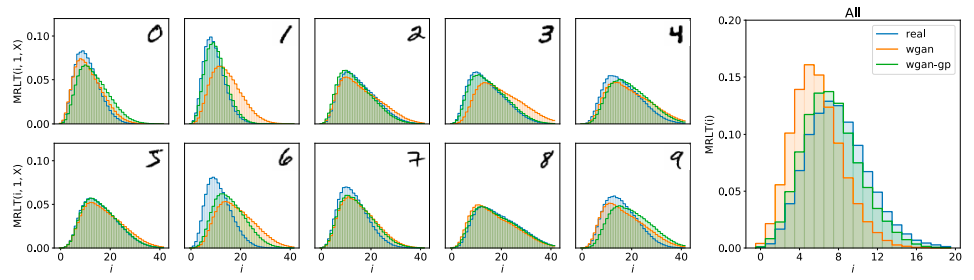
手書き文字のMNISTデータセットにおいて,WGAN,WGAN-GPで学習した結果とデータセットのMRLTの分布,Geometry Scoreは次のようになったという.
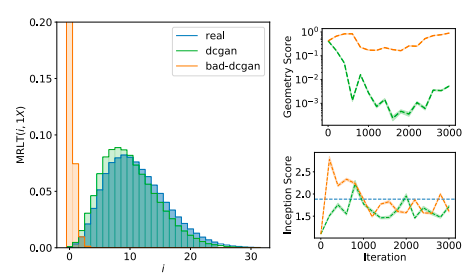
WGANより,WGAN-GPの方がGeometry Scoreが低く元のデータセットと近い分布になっていることが窺える.また,セレブな人のデータCelebAに関して,わざとmode collapseに陥るように作ったDCGAN(bad-dcgan)と通常のDCGAN(dcgan)を比べたところ,次の図のようになったとのことである.
一目瞭然であるが,bad-dcganでは,元のデータセットと分布が程遠い.また,分布が0のあたりに集中していることから,似たデータが多い,すなわちmode collapseに陥っていることがわかる.イテレーション数に対して,Geometry ScoreとInception Scoreを比較したところ,Inception Scoreではdcganもbad-dcganも同じような値を取っており,mode collapseを特定できていないことがわかる.一方,Geometry Scoreでは,mode collapseを捉えている.
最後に
論文の著者は自身のGithub上にGeometry Scoreの実装クラスを挙げており,GUDHI, C++, cython をインストールしていれば python で直ぐにでも動かせる.また,実行時間は$L_0=100$程度であればあっという間に計算が終わるので,大変使いやすい.
TDAを知らない人にも理解してもらえるようにするため,理論は殆ど省いた.指摘等あれば遠慮なく意見して欲しい.また,GANに関しては知っているものとして説明は全くしなかった.興味ある人は,はじめてのGAN,Wasserstein GAN (WGAN) でいらすとや画像を生成してみる等を参照にして欲しい.
参考文献
- Valentin Khrulkov, Ivan Oseledets. 2018. Geometry Score: A Method For Comparing Generative Adversarial Networks. https://arxiv.org/pdf/1802.02664.pdf
- Tim Salimans, Ian Goodfellow, Wojciech Zaremba, Vicki Cheung, Alec Radford, Xi Chen. 2016. Improved Techniques for Training GANs. http://papers.nips.cc/paper/6125-improved-techniques-for-training-gans.pdf
- Christopher Olah. 2014. Neural Network, Manifolds, and Topology. http://colah.github.io/posts/2014-03-NN-Manifolds-Topology/
- 平岡裕章.2013.タンパク質構造とトポロジー: パーシステントホモロジー群入門.共立出版.
- 平岡裕章.2016.位相的データ解析の基礎と応用.http://www.wpi-aimr.tohoku.ac.jp/hiraoka_labo/introduction_j.pdf
- Shinya Yuki. 2017. はじめてのGAN. https://elix-tech.github.io/ja/2017/02/06/gan.html
- Yusuke Ujitoko. 2017. Wasserstein GAN (WGAN) でいらすとや画像を生成してみる.http://yusuke-ujitoko.hatenablog.com/entry/2017/05/20/145924