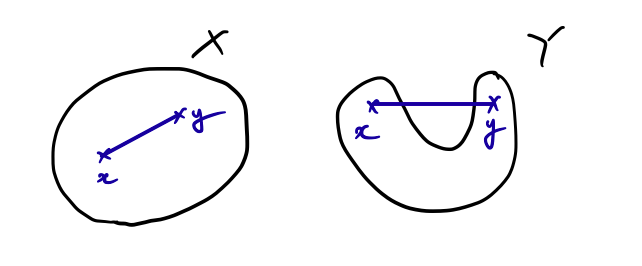本記事では,今年(2018年)9月に DeepMind社 が発表した最適化手法である Hamiltonian Descent Methods (HDMs) に関する解説をし,実装結果を記す.原論文を読み進めるには,凸解析の知識を必要としており,馴染みがない人には読み辛いだろう.実際,日本語の解説記事として唯一見られる記事においても,数学科の人に解説して欲しいと述べられている.
そこで本記事では,まず凸解析の基本事項を述べ,凸解析に馴染みがない人でも読み進められるようにしていく.ただ,凸解析の基礎から述べるため,Qitta の記事としては,比較的長編である.
本記事の構成としては,以下のようになっている.
- HDMs の概要
- 凸解析の基本事項
- 凸集合と凸関数
- エピグラフと閉凸関数
- 凸共役関数と Legendre 変換
- 劣微分と劣勾配
- 強凸関数
- 平滑凸関数
- 強凸関数と平滑凸関数の双対性
- 収束性に関する基本事項
- 連続時間における動的ダイナミクス
- Hamiltonian System
- Conformal Hamiltonian System
- 凸関数に対する CH System の収束性
- 冪関数に対する収束性
- 最適化アルゴリズム
- Implicit Method
- First Explicit Method
- Second Explicit Method
- Multiple Power 関数に対する収束性
- 目的関数の power が既知の場合
- 目的関数の power が未知の場合
HDMs の概要
Hamiltonian Descent Methods (HDMs) では,理論的に最適解へ一次収束するクラスを従来より拡張することができる first order methods (目的関数の1回微分の情報まで使う最適化手法,勾配降下法など)である1.
従来は,強凸かつ平滑であるクラスでしか最適解への一次収束を保証できていないかったが2,HDMs では強凸かつ平滑である関数を含むより広いクラスで最適解への一次収束性を保証している.
しかも,目的関数の2回微分である Hessian が非有界あるいは特異値を有する場合も含んでおり,second order methods (目的関数の2回微分の情報まで使う最適化手法,ニュートン法など)が機能しない場合でも,HDMs は機能し得る.
凸解析の基本事項
本セクションでは,凸解析の基本事項を列挙していく.既にご存知である読者は飛ばして構わない.また,収束レートにしか興味がない読者も読み飛ばして構わない.
凸集合と凸関数
集合$X$が**凸関数(convex set)**であるとは,
$$(\forall x,y\in X)(\forall\theta\in(0,1))\ \theta x+(1-\theta y)\in X$$
であることを言う.言い換えると,$X$内の任意の2点を繋いだ線分が$X$に含まれているということである.例として,次の図を見て欲しい.
集合$X$は任意の2点を繋いだ線分が$X$に含まれているので,凸集合である.一方,集合$Y$は図のように2点 $x,y$ を取ると,2点を繋ぐ線分が集合$Y$に含まれていないので凸集合ではない.平たく言えば,凹みがないのが,凸集合ということになる.
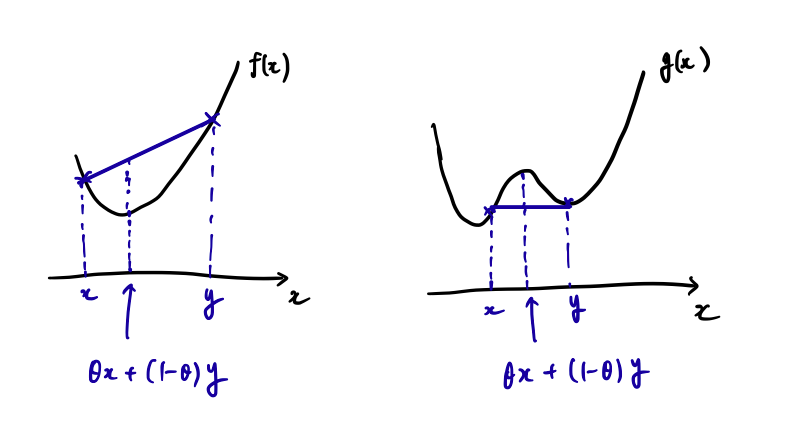
関数 $f:\mathbb{R}^d\to\mathbb{R}_\infty$ が**凸関数(convex function)**であるとは,
$$(\forall x,y\in X)(\forall\theta\in(0,1))\ f(\theta x+(1-\theta)y)\le\theta f(x)+(1-\theta)f(y)$$
であることを言う($\mathbb{R}_\infty=\mathbb{R}\cup\{\infty\}$である).言い換えると,定義域内の任意の2点の間における点での $f$ の値は,2点を通る直線の値以下であるということである.例として,次の図を見て欲しい.
関数 $f$ は,区間$(x,y)$において,関数の値が直線上の値以下であるので,凸関数である.一方,関数$g$ は,直線上の値の方が下に来る場合があり得るので凸関数ではない.平たく言えば,下方向に凹みがないのが凸関数である.
関数 $f:\mathbb{R}^d\to\mathbb{R}_\infty$ が**狭義凸関数(strictly convex function)**であるとは,
$$(\forall x,y\in X)(\forall\theta\in(0,1))\ f(\theta x+(1-\theta)y)<\theta f(x)+(1-\theta)f(y)$$
であることを言う.すなわち,真に2点を結ぶ直線上の値の方が大きい場合である.例えば,$f(x)=|x|$ は凸関数であるが,狭義凸関数ではない.下方向に凹みがないのが凸関数であると述べたが,狭義凸関数は下方向に膨らんでいる必要性がある.
エピグラフと閉凸関数
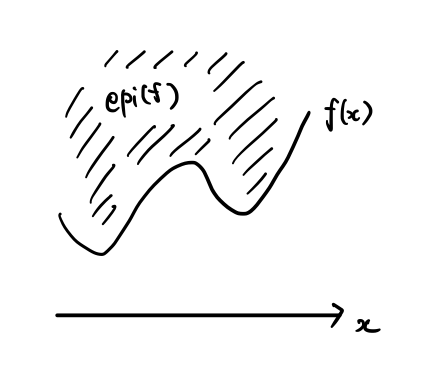
関数 $f:\mathbb{R}^d\to\mathbb{R}_\infty$ の**エピグラフ(epigraph)**は,
$$\mathrm{epi}(f)=\{(x,\mu)\in\mathbb{R}^{d+1}|f(x)\le\mu\}$$
で定義される.分かり易いように,図で書くと,下図のようになる.関数 $f$ の値より上側の領域がエピグラフである.
凸関数 $f:\mathbb{R}^d\to\mathbb{R}_\infty$ が**閉凸関数(closed convex function)であるとは,$\mathrm{epi}(f)$ が閉集合であることを言う.また,$f$ が真凸関数(proper closed convex)**であるとは,$f$ の実行定義域(domain) $\mathrm{dom}(f)=\{x\in\mathbb{R}^d|f(x)<\infty\}$ が空集合でないことを言う.凸解析においては,真閉凸関数(pcc; proper closed convex function) を議論の対象とすることが多い.
凸共役関数と Legendre 変換
関数 $f:\mathbb{R}^d\to\mathbb{R}_\infty$ の**凸共役関数(convex conjugate function)**は,
$$f^*(y)=\sup_{x\in\mathbb{R}^d}\{\langle x,y\rangle-f(x)\}$$
と定義される($\langle\cdot,\cdot\rangle$ はユークリッド空間における自然な内積を表す).また,対応 $f\mapsto f^*$ を **Legendre 変換(Legendre transform)**という.
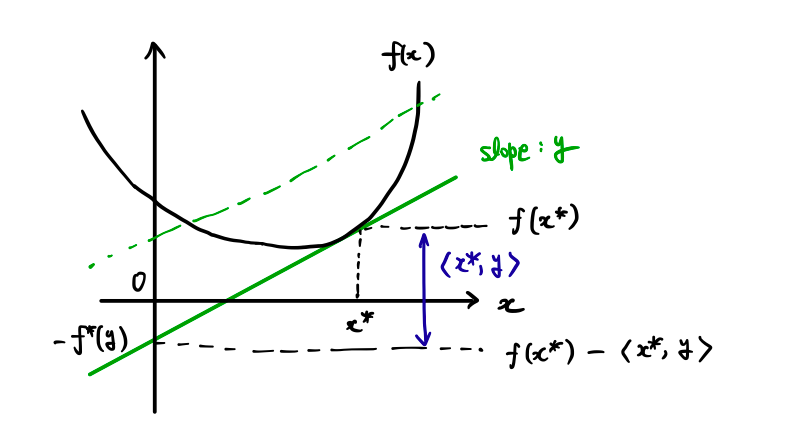
符号を反転させた中の関数を $f_{[y]}(x)=f(x)-\langle x,y\rangle$ とおく.これが最小を達成するためには,微分可能であれば微分が0でなければならないので,
$$\nabla f(x)-y=0$$
より,$y$ は元の関数 $f$ の傾きに対応している.
上の図を見て欲しい.$y$ を与えた時に $f^*(y)$ がどうなるか図式したものである.$f_{[y]}(x)$ に対して,下限(inf)を達成する場合を考察する.$f_{[y]}(x)$ は,$f(x)$ から傾き $y$ の直線に沿って $x=0$ まで持って行った時の切片の値となっている.すなわち,$f_{[y]}(x)$ を最小化させることは,切片における値が最小となるような $x$ を見つけるということになる. これは,元の関数 $f$ の傾きが $y$ となるような $x$ において達成し,その時の切片の値は $-f^*(y)$ となる3.
$f$ が真閉凸関数であれば,$f^{**}=f$ となり,$f$ と $f^*$ が双対な関係にあることが窺える4.
例えば,$f(x)=x^2/2$ の凸共役関数は $f^*(y)=y^2/2$ となる.一般に,$f(x)=|x|^a/a$ の凸共役関数は,$f^*(y)=|y|^b/b,b=a/(a-1)$ になる.この場合の図を示す.
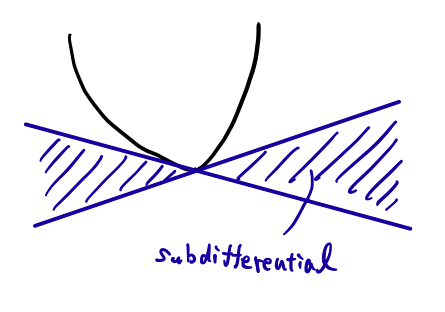
劣微分と劣勾配
真凸関数 $f:\mathbb{R}^d\to\mathbb{R}_\infty$ の $x\in\mathrm{dom}(f)$ における**劣微分(subdifferential)**は,
$$\partial f(x)=\{g\in\mathbb{R}^d|(\forall x'\in\mathbb{R}^d)\langle x'-x,g\rangle+f(x)\le f(x')\}$$
と定義される.また,劣微分の元 $g\in\partial f(x)$ を $f$ の $x$ における劣勾配(subgradient) という.理解のために,下の図を見て欲しい.この関数は,最小値を取る点で微分不可能であるとする.しかし,劣微分は存在し,勾配の左極限と右極限の区間となる.
例えば,$f(x)=|x|$ は $x=0$ で微分不可能である.一方,$x=0$ における劣微分は,
$$\partial f(x)=\{g\in\mathbb{R}^d|(\forall x'\in\mathbb{R}^d)\langle x'-0,g\rangle+|0|\le |x'|\}=[-1,1]$$
となる.このように,劣微分は微分不可能な場合でも微分もどきなものを扱える良いクラスになっている.また,劣微分が1元からなることと,$f$ が $x$ で微分可能なことは同値であることがいえ,その1元は $\nabla f(x)$ となる.さらに,劣微分は,微分と同様に線形性が成り立つことも言える.
$f$ が真閉凸関数であれば,$y\in\partial f(x)$,$x\in\partial f^*(y)$ の同値性が言え,それぞれの劣勾配が対応していることがわかる.
強凸関数
関数 $f:\mathbb{R}^d\to\mathbb{R}_\infty$ が**$\mu$-強凸関数($\mu$-strongly convex function)**であるとは,
$$(\forall x,y\in X)(\forall\theta\in(0,1))\ \frac{\mu}{2}\theta(1-\theta)\|x-y\|^2+f(\theta x+(1-\theta)y)\le\theta f(x)+(1-\theta)f(y)$$
であることをいう($\|\cdot\|$は,ユークリッド空間における自然なノルムである).すなわち,2点間の距離の二乗 $\|x-y\|^2$ に比例する値だけ関数の値を嵩上げしても,まだ直線上の値より小さくなっている.
また,凸関数 $f:\mathbb{R}^d\to\mathbb{R}_\infty$ が $\mu$-強凸であることと,$f(x)-\frac{\mu}{2}\|x\|^2$ が凸関数であることは同値である.すなわち,ノルムの二乗 $\|x\|^2$ だけ関数の凸性を引いても,まだ凸関数になっている.
さらに,真閉凸関数 $f:\mathbb{R}^d\to\mathbb{R}_\infty$ が $\mu$-強凸であることと,
$$(\forall x,y\in\mathrm{dom}(f))(\forall g\in\partial f(x)\neq\emptyset)\ f(x)+\langle y-x,g\rangle+\frac{\mu}{2}\|x-y\|^2\le f(y)$$
が成り立つことは同値である.すなわち,$x$ からその劣勾配 $g$ に沿って $y$ まで移動させ,距離の二乗 $\|x-y\|^2$ に比例する項だけ足しても,まだ $f(y)$ より小さいということである.
最後の説明が一番理解しやすいと思うので,その場合を図示した.$x$ における劣勾配として $g$ を取ってきて,$y$ まで劣勾配に従って持ってきて,追加の項を足しても $f(y)$ で抑えられている.例えば,$f(x)=x^2$ や $f(x)=|x|+x^2$ が挙げられる.
平滑凸関数
実数値凸関数 $f:\mathbb{R}^d\to\mathbb{R}_\infty$ が $L$-平滑凸関数($L$-smooth convex function) であるとは,$f\in C^1(\mathbb{R}^d)$ であり,
$$\|\nabla f(x)-\nabla f(y)\|\le L\|x-y\|$$
であることをいう($C^1(\mathbb{R}^d)$ は,$\mathbb{R}^d$ の任意の点で微分可能な関数全体の集合である).すなわち,勾配 $\nabla f$ がリプシッツ定数 $L$ でリプシッツ連続(Lipschitz continuity)であることをいう(勾配変化量が距離の $L$ 倍で評価できる).
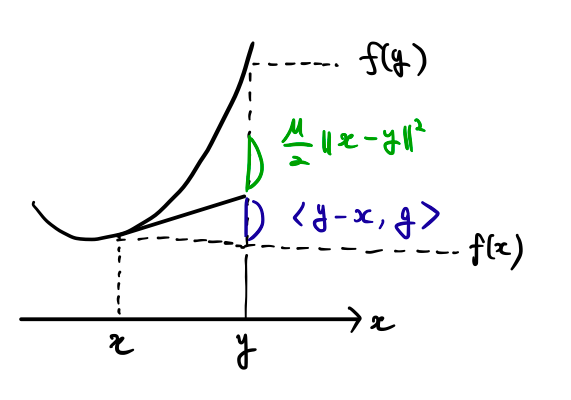
$C^1$級真閉凸関数 $f:\mathbb{R}^d\to\mathbb{R}_\infty$ が $L$-平滑凸関数であることと,
$$(\forall x,y\in\mathbb{R}^d)\ f(y)\le f(x)+\langle y-x,\nabla f(x)\rangle+\frac{L}{2}\|x-y\|^2$$
が成り立つことは同値である.すなわち,$x$ から勾配 $\nabla f(x)$ に沿って $y$ まで移動させた後に,距離の二乗 $\|x-y\|^2$ に比例する項を足すと,必ず $f(y)$ 以上になるということである.
これを図示してみると,上図のようになる.ちょうど強凸性とは双対な性質を持っていることが窺えるのではないだろうか.実際,$f$ が $\mu$-強凸かつ $L$-平滑凸であれば,
$$\frac{\mu}{2}\|x-y\|^2\le f(y)-f(x)-\langle y-x,\nabla f(x)\rangle\le\frac{L}{2}\|x-y\|^2$$
である.すなわち,$x$ から勾配に従って $y$ まで移動させた項を $f(y)$ から引いたものが,下から距離の二乗で抑えているのが強凸性であり,上から距離の二乗で抑えているのが平滑凸性である.例えば,$f(x)=x^2$ や $f(x)=log(1+exp(-x))$ は平滑凸関数である.
強凸関数と平滑凸関数の双対性
真閉凸関数 $f:\mathbb{R}^d\to\mathbb{R}_\infty$ が $\mu$-強凸であることと,その共役凸関数 $f^*$ が $1/\mu$-平滑凸関数であることは,同値である.すなわち,強凸性と平滑凸性は,双対な関係となっている.
収束性に関する基本事項
点列 $\{x_k\}$ は $x^*$ に収束するとする.この時,点列の収束性に関して,次のようなものがある.
点列 $\{x_k\}$ が $x^*$ に**一次収束(linear convergence)**するとは,
$$(\exists c\in(0,1))(\forall k\in\mathbb{N})\ \|x_{k+1}-x^*\|\le c\|x_k-x^*\|$$
が成り立つことである.
点列 $\{x_k\}$ が $x^*$ に**超一次収束(superlinear convergence)**するとは,
$$(\exists\{c_k\}\in(0,1)^\mathbb{N}:c_k\to0(k\to\infty))(\forall k\in\mathbb{N})\ \|x_{k+1}-x^*\|\le c_k\|x_k-x^*\|$$
が成り立つことである.すなわち,収束先に近づくにつれて,収束速度が上がっていく.
点列 $\{x_k\}$ が $x^*$ に**劣一次収束(sublinear convergence)**するとは,
$$(\exists\{c_k\}\in(0,1)^\mathbb{N}:c_k\to1(k\to\infty))(\forall k\in\mathbb{N})\ \|x_{k+1}-x^*\|\le c_k\|x_k-x^*\|$$
が成り立つことである.すなわち,収束先に近づくにつれて,収束速度が落ちていく.
これらは,次のように表すこともできる.
\{x_k\}:\text{superlinear}\Leftrightarrow\lim_{k\to\infty}\frac{\|x_{k+1}-x^*\|}{\|x_k-x^*\|}=0\\
\{x_k\}:\text{linear}\Leftrightarrow\lim_{k\to\infty}\frac{\|x_{k+1}-x^*\|}{\|x_k-x^*\|}=c\ (\exists c\in(0,1))\\
\{x_k\}:\text{sublinear}\Leftrightarrow\lim_{k\to\infty}\frac{\|x_{k+1}-x^*\|}{\|x_k-x^*\|}=1\\
HDMs においては,とりわけ linear convergence するクラスを扱っていく.
連続時間における動的ダイナミクス
既に読み疲れている方もいるかもしれないが,ここからが本論である.原論文に従って,Hamiltonian system, Conformal Hamiltonian system について説明したのちに,CH system が満たす性質を紹介していく.証明は一切行わないので,気になる方は原論文を参考にして欲しい.
Hamiltonian System
原論文では,いきなり Hamiltonian system を記述しているが,解析力学に疎い読者のために Hamiltonian の説明からしていく.座標 $x$,質量 $m=1$ の物体に対して力 $F$ が働いている時,運動方程式は,
$$F=\frac{d^2x}{dt^2}=x''$$
と記述できる5.ここで,力 $F$ のポテンシャル $U$ を考えると,
$$F=-\mathrm{grad}U=x''$$
と書ける6.また,この系のエネルギーは,
$$E=\frac{1}{2}\|x'\|^2+U(x)=\frac{1}{2}\|p\|^2+U(x)$$
と記述できる.ここで,$p=mx'=x'$ は運動量である.
Newton の運動方程式は座標 $x$ に依存して,方程式の形が変化してしまう.すなわち,$x$の座標変換に対して頑健でない7.そこで,座標変換に頑健な Lagrangean や Hamiltonian が提唱された.中でも,Hamiltonian の運動方程式(正準方程式)は,任意の正準変換に対して,方程式の形が不変であるという非常に良い性質を持つ.
Lagrangean は,運動エネルギー $T$,ポテンシャル $U$ に対して,$L=T-U$ と定義される.Lagrangean は $x$ に関する任意の座標変換に対して,Lagrange の運動方程式の形が変わらないという良い性質を持つ.しかし,運動量 $p$ と座標 $x$ の間には,$p=x'$ という束縛があり,$x,p$ を独立に座標変換するということはできない8.
Lagrangean が与えられた時,座標 $x$ に対して**共役運動量(conjugate momentum)**として,
$$p=\frac{\partial L}{\partial x}$$
が定義される($p$ を先ほどの運動量と同じ記号で書いており,abuse of notation であるが,以降文中の $p$ は共役運動量である).すると,この共役運動量と Lagrangean を用いて,Hamiltonian は,
$$H(x,p)=\langle p,x'\rangle-L(x',x)$$
と定義される.すると,**正準方程式(canonical equation)**と呼ばれる次式が成立する.
x'=\nabla_p H(x,p)\\
p'=-\nabla_x H(x,p)
正準方程式は,系の座標 $x$,共役運動量 $p$ の時間変化を記述する運動方程式であり,しかも**正準変換(canonical transform)**と呼ばれるクラスの変換で形が不変である.正準変換は,Lagrangean が許す変換(共役運動量を運動量とみなした時の $x$ に関する任意の座標変換)を含む広いクラスである.
また,共役運動量を $p=mx'=x'$ とみなし,座標 $x$ として直交座標を持ってこれば,Hamiltonian は,
$$H=T(p)+U(x)=\frac{1}{2}\|p\|^2+U(x)$$
となり,Newton で考えた場合の全エネルギーに一致する.このように一般に,Hamiltonian は系の全エネルギーを表す.
全エネルギーを表す Hamiltonian の最小化と目的関数 $f$ の最小化を上手く対応させたのが,Hamiltonian Descent Methods ということになる.位置 $x_t:[0,\infty)\to\mathbb{R}^d$,運動量 $p_t:[0,\infty)\to\mathbb{R}^d$ を時間 $t$ に対する関数とする.運動エネルギーを $k:\mathbb{R}^d\to\mathbb{R}$ とすると,Hamiltonian system を,
$$H(x,p)=k(p)+f(x)-f(x^*)$$
とする.運動エネルギー $k$ として,狭義凸関数であり,$k(0)=0$ で最小となるものを選べば,これが解析力学の運動エネルギーに対応する9.また,$f_c(x)=f(x)-f(x^*)$ とすると,これは $x=0$ で最小値0を取り,解析力学のポテンシャルに対応する.系の時間発展は,正準方程式から,
x_t'=\nabla_p H(x_t,p_t)=\nabla k(p_t)\\
p_t'=-\nabla_x H(x_t,p_t)=-\nabla f(x_t)
と記述できる.Hamiltonian system はエネルギー保存則が成り立ち,
$$H_t'=\langle\nabla k(p_t),p_t'\rangle+\langle\nabla f(x_t),x_t'\rangle=0$$
となる.
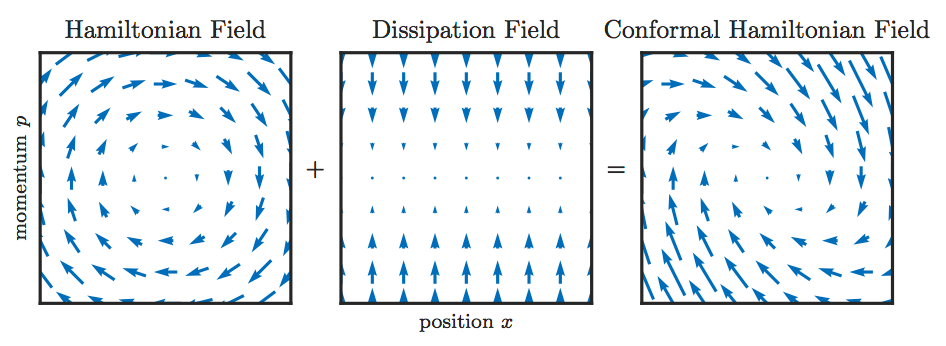
Conformal Hamiltonian System
Hamiltonian system では,エネルギーが保存されているため,Hamiltonian が減少せず,$f$ を減少させることができない.そこで,**散逸系(Dissipation system)**として,系に摩擦力 $\gamma p_t$ を導入した Conformal Hamiltonian system (CH system)
x_t'=\nabla k(p_t)\\
p_t'=-\nabla f(x_t)-\gamma p_t
を考える10.ただし,$\gamma\in(0,\infty)$ である.すると,Hamiltonian の時間変化は,
$$H_t'\langle\nabla k(p_t),p_t'\rangle+\langle\nabla f(x_t),x_t'\rangle=-\langle\nabla k(p_t),p_t\rangle\le-\gamma k(p_t)\le0$$
となる.ここで,$k$ が凸関数であることと $k(0)=0$ であることを用いた.図では,次のように表せる.
CH system において,$\nabla f,\nabla k$が連続,$H$が放射非有界であれば,任意の初期値 $(x_0,p_0)\in\mathbb{R}^{2d}$ に対して,任意の時刻 $t\ge0$ で解の存在が言える.また,$\nabla f,\nabla k$ が連続微分可能であれば,解は一意に定まる.ここで,$f:\mathbb{R}^n\to\mathbb{R}^m$ が**放射非有界(radially unbounded)**であるとは,$\|x\|\to\infty\Rightarrow\|f(x)\|\to\infty$ であることをいう.
$x_t,p_t$ を CH system の解とするとき,$k$ が連続微分可能,$f$ が下に有界,$H$ が放射非有界であれば,$t\to\infty\Rightarrow\|\nabla f(x_t)\|_2\to0$ が言える.ここで,ノルムの下付き添え字 $q$ は $l^q$ ノルム
\|x\|_q=\left(\sum_{k=1}^d |x_k|^q\right)^{1/q}
を表し,$q=2$ は自然なユークリッドノルムである.
これらの命題から,適当な緩い条件下で CH system は解を持ち,しかも $f$ は最適解に収束する11.
凸関数に対する CH system の収束性
CH system を用いれば,$f$ が最適解へ収束することは述べたが,linear convergence を達成するわけはない.そこで,$f$ を凸関数の場合に限定したとき,Lyapunov 関数を構成し,linear convergence を達成することを概観する.
力学系では,系の安定性を議論するために Lyapunov 関数が用いられる.系の平衡点 $x^*$ に対し, 次の性質を満たす関数 $\nu:\mathbb{R}^d\to\mathbb{R}$ を Lyapunov 関数という.
\forall x\neq x^*,\ \nu(x)>0,\ \nu(x^*)=0\\
\forall x\neq x^*,\ \nu'(x)<0,\ \nu(x^*)=0
Lyapunov 関数を構成することができれば,最適解以外では常に減少し続けて最適解に収束する**大域的漸近安定性(globally asymptotically stability)**が言える.CH system の Hamiltonian は,$p_t=0$ になったら $H_t'=0$ となり,Lyapunov 関数とはならない.そこで,$\beta\in(0,\gamma)$ に対して,
$$\nu(x,p)=H(x,p)+\beta\langle x-x^*,p\rangle$$
とすると,これは Lyapunov 関数となる.
$\alpha\in(0,1],\beta\in(0,\alpha]$ に対して,
k(p)\ge\alpha f^*_c(-p)\Rightarrow \frac{\alpha-\beta}{\alpha}H(x,p)\le\nu(x,p)\\
k(p)\ge\alpha f^*_c(p)\Rightarrow \nu(x,p)\le\frac{\alpha+\beta}{\alpha}H(x,p)
が成り立つ.すなわち,Lyapunov 関数 $\nu$ を Hamiltonian で評価することができる. この両者が成り立つ時に,linear convergence を達成できる.
ここで,linear convergence を達成するための仮定(Assumption A)を列挙する.
A.1. $f:\mathbb{R}^d\to\mathbb{R}$ が微分可能,凸関数,$x^*$ で一意の最小解.
A.2. $k:\mathbb{R}^d\to\mathbb{R}$ が微分可能,狭義凸関数,$k(0)=0$ で最小解.
A.3. $\gamma\in(0,1)$
A.4. 微分可能単調減少凸関数 $\alpha:[0,\infty)\to(0,1]$ と定数 $C_{\alpha,\gamma}\in(0,\gamma]$ が存在し,
k(p)\ge\alpha(k(p))\max\{f_c^*(p),f_c^*(-p)\}\ (\forall p\in\mathbb{R}^d)\\
-C_{\alpha,\gamma}\alpha'(y)y<\alpha(y)\ (\forall y\in[0,\infty))
ここで,$\alpha$ は定数でも良いが,最適解に近付くにつれて $\alpha$ を大きく取れるようになり,収束速度が上がるという好ましい性質があるため,$\alpha$ を関数として扱う方が良い.これらの仮定のもとで,
$$f(x_t)-f(x^*)\le 2H_0\exp(-\lambda\alpha_* t)$$
であることが示される.ここで,$\lambda=(1-\gamma)C_{\alpha,\gamma}/4$,$H_0=f(x_0)-f(x^*)$,$\alpha_*=\alpha(3H_0)$ である.すなわち,目的関数 $f$ の linear convergence をいうことができる.これは,$f(x_t)-f(x^*)=e^{-\lambda\alpha_*t}$ の状況を考えた時,
$$\lim_{t\to\infty}\frac{f(x_{t+1})-f(x^*)}{f(x_t)-f(x^*)}=e^{-\lambda\alpha_*}$$
となることから,linear convergence と言っている.
冪関数に対する収束性
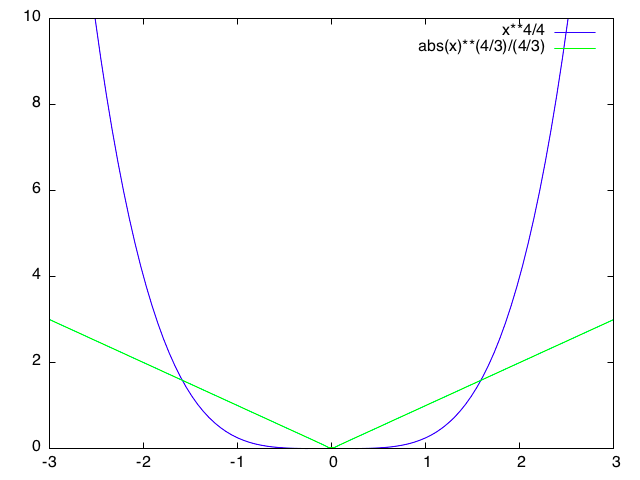
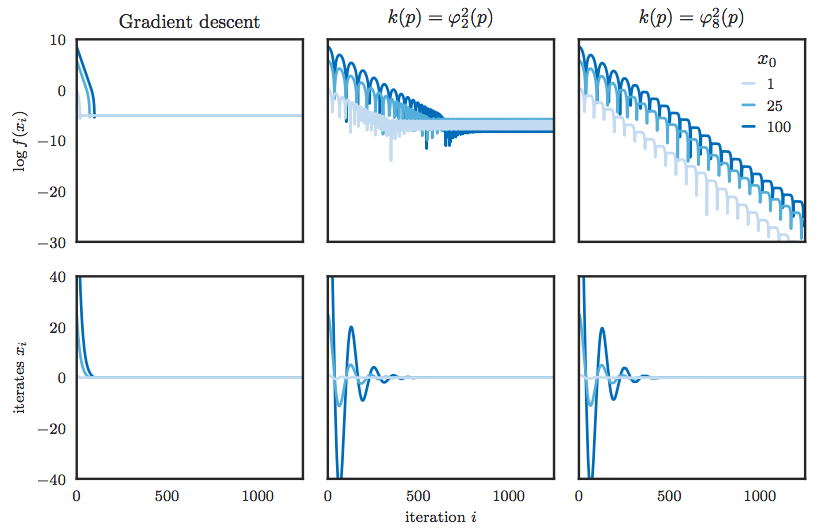
特に,冪関数 $k(p)=|p|^a/a$,$f(x)=|x|^b/b$ の場合の収束性について見ていく.$1/a+1/b\ge1$ の場合,先ほどの Assumption A を満たし,linear convergence を達成する.$a/1+1/b<1$ の場合は,$|x_t^{-1}|$ の収束レートが $O(t^{1/(ba-b-a)})$ となり,sublinear convergence を達成することが示せる.以上の結果を図でまとめると,下図のようになる(1st explicit method, 2nd explicit method に関しては後述する).
例えば,$b=4$ を取り, $f(x)=x^4/4$ とした場合に,$1/a+1/b=1$ を満たす $a=4/3$ と,$1/a+1/b<1$ となる $a=2$ を選んだ場合の収束性の違いを見てみる.下図のように,$a=4/3$ では一定の速度で収束している(linear convergence)が,$a=2$ では最適解の近くで収束速度が落ちている(subliner convergence).
最適化アルゴリズム
漸く最適化アルゴリズムの話に入る.論文では,Implicit Method, First Explicit Method, Second Explicit Method の3つの方法を紹介している.Implicit Method は linear convergence を達成する仮定が緩いものの部分問題を解かなければならず,Explicit Methods では linear convergence を達成する仮定が厳しいが陽に時間発展させることができる.それぞれの良し悪しを抑えて,問題に応じて使い分けることが求められるだろう.
Implicit Method
Implicit Method では,CH system の左辺を
x_t'=\frac{x_{i+1}-x_i}{\varepsilon},\ p_t'=\frac{p_{t+1}-p_t}{\varepsilon}
と近似し右辺を時刻 $i+1$ の点 $(x_{i+1},p_{i+1})$ とした場合であり,
\frac{x_{i+1}-x_i}{\varepsilon}=\nabla k(p_{i+1})\\
\frac{p_{t+1}-p_t}{\varepsilon}=-\gamma p_{i+1}-\nabla f(x_{i+1})
と表せる12.この系の更新式は,$\varepsilon,\gamma\in(0,\infty),\delta=(1+\gamma\varepsilon)^{-1}$ に対して,次のように表せる.
x_{i+1}=\mathrm{arg}\min_{x\in\mathbb{R}^d}\{\varepsilon k^*\left(\frac{x-x_i}{\varepsilon}\right)+\varepsilon\delta f(x)-\delta\langle p_i,x\rangle\}\\
p_{i+1}=\delta p_i-\varepsilon\delta\nabla f(x_{i+1})
$f,k$ が Assumption A.1,A.2 を満たしていれば,これは一意の解を持つことが言える.また,次の Assumption B が成り立てば,linear convergence も言える.
B.1. ある $C_{f,k}\in(0,\infty)$ が存在し,任意の $x,p\in\mathbb{R}^d$ に対して,
$$|\langle\nabla f(x),\nabla k(p)\rangle|\le C_{f,k}H(x,p).$$
これは,$\nabla f,\nabla k$ の内積が Hamiltonian $H$ で評価することができる,すなわち,極端な変化が起こらないことを要請している(以降,Explicit Methods で Assumption C,D と出てくるが,ふ〜んぐらいで見てくれれば良い.取り敢えず極端な変化を嫌っているんだなあっていうテンションであれば良い).Assumption B は比較的緩い条件下で成立する.例えば,$f$ が平滑凸関数,$k$ が classical momentum $k(p)=\|p\|^2/2$ の場合が挙げられる13.
Assumption A,B の下で,$\varepsilon=(1-\gamma)/(2\max(C_{f,k},1))$ とすると,
$$f(x_t)-f(x^*)\le 2H_0\left[1+\varepsilon C_{\alpha,\gamma}(1-\gamma-2C_{f,k}\varepsilon)\alpha_*/4\right]^{-i}$$
であることが示され,Implicit Method が linear convergence であると言える(右辺がぐちゃぐちゃしているが,[~]の中身は $>1$ なので,その $-1$ 乗は $(0,1)$ に収まり,linear convergence の定義を満足していることが分かる.以降出てくる式も右辺がぐちゃぐちゃしているが $-i$ 乗している中身が $>1$ なので,linear convergence をいうことができる).Implicit Method はこのように少ない仮定の下で linear convergence を示せるが,$x$ の更新式において argmin の部分問題を解く必要性がある.
First Explicit Method
First Explicit Method では,CH system の左辺を
x_t'=\frac{x_{i+1}-x_i}{\varepsilon},\ p_t'=\frac{p_{t+1}-p_t}{\varepsilon}
と近似し右辺を $(x_i,p_{i+1})$ とした場合であり,
\frac{x_{i+1}-x_i}{\varepsilon}=\nabla k(p_{i+1})\\
\frac{p_{t+1}-p_t}{\varepsilon}=-\gamma p_{i+1}-\nabla f(x_i)
と表せる.これは,形を変形すれば,
p_{i+1}=\delta p_i-\varepsilon\delta\nabla f(x_i)\\
x_{i+1}=x_i+\varepsilon\nabla k(p_{i+1})
と表せ,陽に更新していくことができる.しかし,右辺を時点が異なる $(x_i,p_{i+1})$ で近似したために,$\nabla f$ が急激に変化しないようにする条件が必要となる.次の Assumption C が成り立てば,linear convergence をいうことができる.
C.1. ある $C_k\in(0,\infty)$ が存在し,任意の $p\in\mathbb{R}^d$ に対して,
$$\langle\nabla k(p),p\rangle\le C_k k(p).$$
C.2. $f:\mathbb{R}^d\to\mathbb{R}$ が凸関数,$x^*$ で一意の最小解,$x^*$ 以外で2回連続微分可能.
C.3. ある $D_{f,k}\in(0,\infty)$ が存在し,任意の $p\in\mathbb{R}^d,x\in\mathbb{R}^d\setminus\{x^*\}$ に対し,
$$\langle\nabla k(p),\nabla^2f(x)\nabla k(p)\rangle\le D_{f,k}\alpha(3H(x,p))H(x,p).$$
この Assumption C の下で,
$$0<\varepsilon<\min\left(\frac{1-\gamma}{2\max(C_{f,k}+6D_{f,k}/C_{\alpha,\gamma},1)},\frac{C_{\alpha,\gamma}}{10C_{f,k}+5\gamma C_k}\right)$$
なる $\varepsilon$ に対して,
$$f(x_t)-f(x^*)\le 2H_0\left(1+\frac{\varepsilon C_{\alpha,\gamma}}{4}[1-\gamma-2\varepsilon(C_{f,k}+6D_{f,k}/C_{\alpha,\gamma})\alpha_*]\right)^{-i}$$
が示せて,linear convergence が言える(こんな複雑なものは,ふ〜んっていうテンションである.まあ右辺の大きい括弧の中は $>1$ だし,linear convergence だろっていうテンションで良い).
凸関数の場合だけ述べており,他の関数に対する収束性はどうなのかと気になるかもしれない.実際,linear convergence についてはいうことができないが,uniformly smoothness という比較的広いクラスの関数で,First Explicit Method は最適解への収束が示されている.
Second Explicit Method
Second Explicit Method では,今度は右辺を $(x_{i+1},p_i)$ とした場合であり,
\frac{x_{i+1}-x_i}{\varepsilon}=\nabla k(p_i)\\
\frac{p_{t+1}-p_t}{\varepsilon}=-\gamma p_i-\nabla f(x_{i+1})
と表せる.これは,形を変形すれば,
x_{i+1}=x_i+\varepsilon\nabla k(p_i)\\
p_{i+1}=(1-\varepsilon\gamma)p_i-\varepsilon\nabla f(x_{i+1})
と表せ,陽に更新していくことができる.今度は,$\nabla k$ に急激な変化しないようにするための条件等が必要になり,linear convergence を達成するには,次の Assumption D が必要になる.
D.1. $k:\mathbb{R}^d\to\mathbb{R}$ は狭義凸関数,$k(0)=0$ で最小,0以外で2回微分可能.
D.2. ある $C_k\in(0,\infty)$ が存在し,任意の $p\in\mathbb{R}^d$ に対して,
$$\langle\nabla k(p),p\rangle\le C_kk(p).$$
D.3. ある $D_k\in(0,\infty)$ が存在し,任意の $p\in\mathbb{R}^d\setminus\{0\}$
$$\langle p,\nabla^2k(p)p\rangle\le D_kk(p).$$
D.4. ある $E_k,F_k\in(0,\infty)$ が存在し,任意の $p,q\in\mathbb{R}^d$ に対して,
$$k(p)-k(q)\le E_kk(q)+F_k\langle\nabla k(p)-\nabla k(q),p-q\rangle.$$
D.5. ある $D_{f,k}\in(0,\infty)$ が存在し,任意の $x\in\mathbb{R}^d,p\in\mathbb{R}^d\setminus\{0\}$ に対して,
$$\langle\nabla f(x),\nabla^2k(p)\nabla f(x)\rangle\le D_{f,k}\alpha(3H(x,p))H(x,p).$$
もう Assumption が多過ぎて,ふ〜んという気分を通り越してしまって条件厳し過ぎね?って思い始めているかもしれない.だけど,$k$ は適切なものを自分で選べば良いだけなので,$f$ に関する条件に比べれば大したことはない.Assumption A,B,D の下で,
$$0<\varepsilon<\min\left(\frac{1-\gamma}{2(C_{f,k}+6D_{f,k}/C_{\alpha,\gamma})},\frac{1-\gamma}{8D_k(1+E_k)},\frac{C_{\alpha,\gamma}}{6(5C_{f,k}+2\gamma C_k)+12\gamma C_{\alpha,\gamma}},\sqrt{\frac{1}{6\gamma^2D_kF_k}}\right)$$
なる $\varepsilon$ に対して,
$$f(x_t)-f(x^*)\le 2H_0\left(1-\frac{\varepsilon C_{\alpha,\gamma}}{4}[1-\gamma-2\varepsilon(C_{f,k}+6D_{f,k}/C_{\alpha,\gamma})]\alpha_*\right)^i$$
となり,linear convergence を達成する(右辺の大きい括弧の中身が今までと違って $<1$ であり,代わりに $i$ 乗となっていることに注意されたい).
Multiple Power 関数に対する収束性
目的関数の power が既知の場合
さて,最適化アルゴリズムについて色々述べてきたが,具体的な関数については言及していなかった.ここでは,具体的な関数として multiple power 関数に対する検証と,そこから一般の関数に対してどのような場合に収束性が言えるのか述べていく.
multiple power 関数とは,定数 $a,A\in[1,\infty)$ に対して,
$$\varphi_a^A(t)=\frac{1}{A}(t^a+1)^{A/a}-\frac{1}{A}\ (t\in[0,\infty])$$
である.一見,複雑であるが,少し考察すれば,グラフの底(body)に近づくと $a$ 乗関数のように振る舞い,グラフの端(tail)に近づくと $A$ 乗関数のように振る舞う関数である.例として,次の図を見てみれば,その様子が顕著であろう.
ここで,$f,k$ の power に特定の関係があれば,それぞれの Method の linear convergence の Assumption を満たすことが言える.$f(x)=\varphi_b^B(\|x\|)$ であれば,次のように運動エネルギー $k$ の power を選べば,Assumption を達成する.
| method | f:body power | f:tail power | k:body power | k:tail power |
|---|---|---|---|---|
| implicit | $b>1$ | $B>1$ | $a=b/(b-1)$ | $A=B/(B-1)$ |
| 1st explicit | $b\ge2$ | $B\ge2$ | $a=b/(b-1)$ | $A=B/(B-1)$ |
| 2nd explicit | $1<b\le2$ | $1<B\le2$ | $a=b/(b-1)$ | $A=B/(B-1)$ |
すなわち,$f$ の power を知ってさえいれば,それに適した $k$ の power $a,A$ と手法を選択することで,linear convergence を達成することが言える.これは,$f$ が $\varphi_b^B$ でなくとも,body や tail で power が $b,B$ になっていればいうことができる.
では,$a=b/(b-1)\Leftrightarrow 1/a+1/b=1$ のようなチョイスは何で選ばれているのであろうか.勘の鋭い人は,凸共役関数を説明した時に,power 関数 $f(x)=|x|^a/a$ の凸共役は $f^*(y)=|y|^b/b,b=a/(a-1)$ であったことを思い出すかもしれない.さらに,Assumption A.4 で $k^(p)\ge\alpha\max\{f_c^*(p),f_c^*(-p)\}$ が必要だと言っていたことも思い出すかもしれない.ここまで思い出せば,$k=f^$ が達成するのが $1/a+1/b=1$ であることがわかる.さて,図でこの結果をまとめると次のようになる.
これは,以前にも一度出した図であるが,その時は Explicit Methods の部分の説明はしていなかった.$a=b=2$ が最適なチョイスであり,$1/a+1/b=1$ の曲線上であれば Implicit Method の Assumption B が成立する.また,曲線上 $b\ge2$ であれば 1st explicit method の Assumption Cが,$1<b\le2$ であれば 2nd explicit method の Assumption D が成立する.
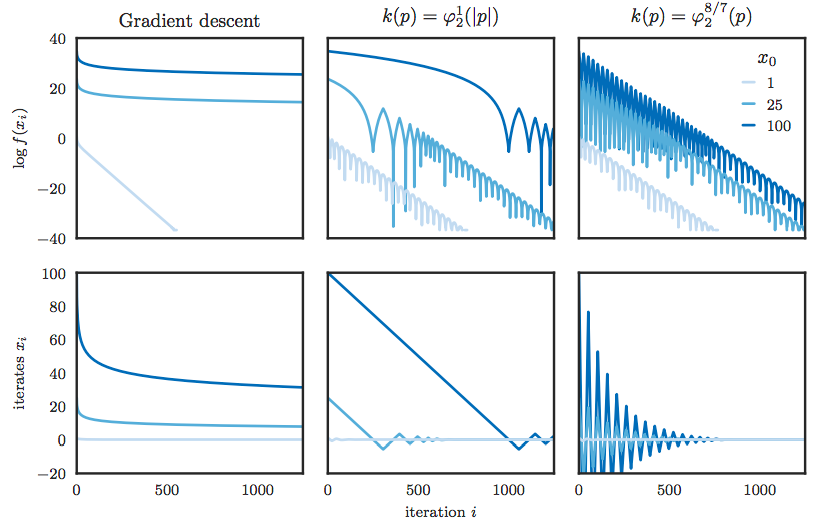
例として,通常の Gradient Descent では最適化が難しい $f(x)=\varphi_{8/7}^2(x)$ を取り上げる.この時,Gradient Descent, classical momentum, second explicit method ではそれぞれ次のような振る舞いを示したと主張している.見ての通り,GD や classical momentum では最適解へ収束していないが,second explicit method では,最適解へ一定レートで収束していることが見て取れる.
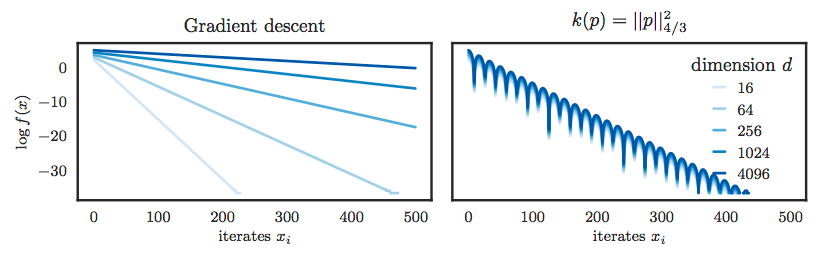
また,GD 法など多くの方法では,linear convergence を達成する場合でも次元が上がると格段に収束速度が落ちるという問題があるが,Hamiltonian Descent Methods では次元の増加に頑健であり,例えば,$f(x)=\|x\|_4^2/2$ とした場合,次のような結果が得られたと示されている.見ての通り,GD 法は次元の増加に弱いが,HDMs では次元の増加を諸共しない.これは,収束レート(linear convergence を示した時の右辺のぐちゃぐちゃしたところ)に次元の項が一切現れていないからである.
目的関数の power が未知の場合
しかし,目的関数 $f$ の body,tail における振る舞いがわかっているというケースは現実の問題においては少ない.$f$ の power の情報がわからない時,どう $k$ を選べば良いのかという問題に陥る.この場合でも body での power が $b=2$ の場合に限定すれば,tail での power が未知 $B\ge2$ でも implicit method, 1st explicit method は linear convergence を達成する.先ほどの表を拡張すると,
|method|power|f:body power|f:tail power|k:body power|k:tail power|
|---|---|---|---|---|
|implicit|known|$b>1$|$B>1$|$a=b/(b-1)$|$A=B/(B-1)$|
|implicit|unknown|$b=2$|$B\ge2$|$a=2$|$A=1$|
|1st explicit|known|$b\ge2$|$B\ge2$|$a=b/(b-1)$|$A=B/(B-1)$|
|1st explicit|unknown|$b=2$|$B\ge2$|$a=2$|$A=B/(B-1)$|
|2nd explicit|known|$1<b\le2$|$1<B\le2$|$a=b/(b-1)$|$A=B/(B-1)$|
となる.このように,運動エネルギー $k$ としては,$k(p)=\varphi_2^1(\|p\|)=\sqrt{\|p\|^2+1}-1$ を選んでしまえば良い.この運動エネルギーは relativistic kinetic と呼ばれ,微分すると,
$$\nabla k(p)=\frac{p}{\sqrt{\|p\|^2+1}}$$
となり,様々な適応的勾配降下法で使われている形になる.実際,$f(x)=\varphi_2^8(x)$ が真の場合,$f$ の tail での power を知らないとして,relativistic kinetic を選んだ場合の結果は次のようになったと示されている.relativistic kinetic では最初こそスローペースなものの,途中から一気に加速し,最適解に収束している様子が見て取れる.
まとめ
まとめると,
- HDMs には3種類の方法があり,使い分けが大事!
- HDMs では,今までより広範なクラスで linear convergence の達成を示せる!(今までの GD 法などは,強凸性,平滑凸性が必要な狭いクラスであった)
- 目的関数 $f$ の最適解近傍での振る舞いさえわかれば,linear convergence を達成することができる!
今後の課題としては,
- より広いクラスで linear convergence 達成したい!
- 目的関数 $f$ の最適解近傍での振る舞いを,一般の機械学習や深層学習のシチュエーションでどうやって特定するか
実装に関するコメント
- python とかであれば自動微分が備わっているので,explicit methods の実装は容易いだろう.
- implicit method の実装は,部分問題の解き方に依存しそう.
記事を書いたコメント
- 長文読んでくださってありがとうございます.
- 長文なので,誤植もありそうです.ぜひ指摘してください.
- 数学の証明をふわっと感覚だけ述べて無視したので,興味ある人は原論文読んで見てください.
参考文献
- Chris J. Maddison, Daniel Paulin, Yee Whye Tec, Brendan O’Donoghue and Arnaud Doucet. Hamiltonian Decent Methods. 2018. https://arxiv.org/pdf/1809.05042.pdf
- Hamed Karimi, Julie Nutini and Mark Scdmidt. Linear Convergence of Gradient and Proximal-Gradient Methods Under the Polyak-Lojasiewicz Condition. 2018. https://arxiv.org/pdf/1608.04636.pdf
- R. Tyrrell Rockfellar. Convex Analysis. 1970. Princeton University Press, 1970.
- Amir Beck. First-Order Methods in Optimization. Society for Industrial and Applied Mathematics. 2017.
- 鈴木大慈,機械学習プロフェッショナルシリーズ 確率的最適化,講談社,2015.
- 山下信雄,非線形計画法 (応用最適化シリーズ6),朝倉書店,2015.
- Steven H. Strogatz 著,田中久陽・中尾裕也・千葉逸人訳,ストロガッツ 非線形ダイナミクスとカオス,丸善出版,2015.
- Morris W. Hirsch, Stephen Smale, Robert L. Devaney 著,桐木紳・三波篤郎・谷川清隆・辻井正人訳,Hirsch・Smale・Devaney 力学系入門 ー微分方程式からカオスまでー 原著第3版,共立出版,2017.
- 山た一・優曇華院.Hamiltonian Descent Methodsの実装についての解説.2018.https://omedstu.jimdo.com/2018/09/26/hamiltonian-descent-methods%E3%81%AE%E5%AE%9F%E8%A3%85%E3%81%AB%E3%81%A4%E3%81%84%E3%81%A6%E3%81%AE%E8%A7%A3%E8%AA%AC/
-
HDMs の First Explicit Method は,linear convergence の条件に Hessian を用いるが first order methods である. ↩
-
近年,H. Karimi et al. によって,強凸性より広い Polyak-Lojasiewicz Condition での一次収束性が示された.詳しくは,[2]を見よ. ↩
-
$f$ が微分不可能な場合は,$y$ が $f$ の劣勾配に対応する. ↩
-
数学で,双対(dual)というときは,コインの表裏のようにお互いをひっくり返すともう一方になるようなことを言う. ↩
-
時間微分にはドット($\dot x$)を使うべきだと思うが,原論文でダッシュ(x')を使っているため,それに統一する. ↩
-
数学においてポテンシャルは,$F=\mathrm{grad}U$ と定義することが多いが,物理ではマイナスをつけて定義することが多い. ↩
-
例えば,3次元の極座標変換を考えると,非常に複雑な形になることがわかる. ↩
-
Lagrangean なので,$x$ は一般化座標であり,$q$ と表すべきであるが,これも原論文が $x$ と記載されていることに統一している. ↩
-
運動エネルギーが運動エネルギーに対応する,という言葉の濫用をしているが,それぞれ Hamiltonian system の運動エネルギー,解析力学の運動エネルギーを指している. ↩
-
散逸系とは,文字通りエネルギーが散逸していく系である. ↩
-
これらの命題の証明には,Peano の存在定理,LaSalle の原理を用い,微分方程式・力学系の知識が必要となる. ↩
-
差分法を知っていれば,これが後退 Euler 法であることが分かる.後退 Euler 法は,一般に陰的解法(implicit method)となるが,安定性が高いことが知られており,制約が少なく済む. ↩
-
classical momentum と言っているのは,物理的な運動エネルギーと同じ形式の運動エネルギーだからである. ↩