AtCoder ABC267 C問題 詳解
ABC267 C問題の公式解説が物足りなかったため、備忘録の意味も込めて詳解を投稿します。
問題
長さNの整数列A=(A_{1},A_{2},...,A_{N})が与えられます。\\ 長さMのAの連続部分列B=(B_{1},B_{2},...,B_{M})に対する、 \sum_{i=1}^{M}i×B_{i} の最大値を求めてください。
すなわち、
f(x)=1×A_{x}+2×A_{x+1}+\dots+M×A_{x+M-1}, (1\leq x\leq N-M+1)\\
の最大値を求める問題です。
詳解
総当たりの場合
まず、総当たりを考えます。
$f(1)$から$f(N-M+1)$を全て計算した後、最大値を求めればよいです。
このとき、$f(x)$を求めるのに$M(\leq N)$回加算を行い、その操作を$(N-M+1)$回行うので計算量は
O(M)×O(N-M+1)\leq O(N)×O(N-M+1) = O(N^2)
となります。$O(N^2)$より当然TLEとなるので工夫が必要です。
工夫
TLEとなる原因は、$O(N)$の計算を繰り返すことです。
これを回避するために$f(x+1)$を$f(x)$を用いて求められるようにする必要があります。
そのために次の工夫を考えます。
g(x)=A_{x}+A_{x+1}+\dots+A_{x+M-1}, h(x)=M×A_{x+M-1}
とすると
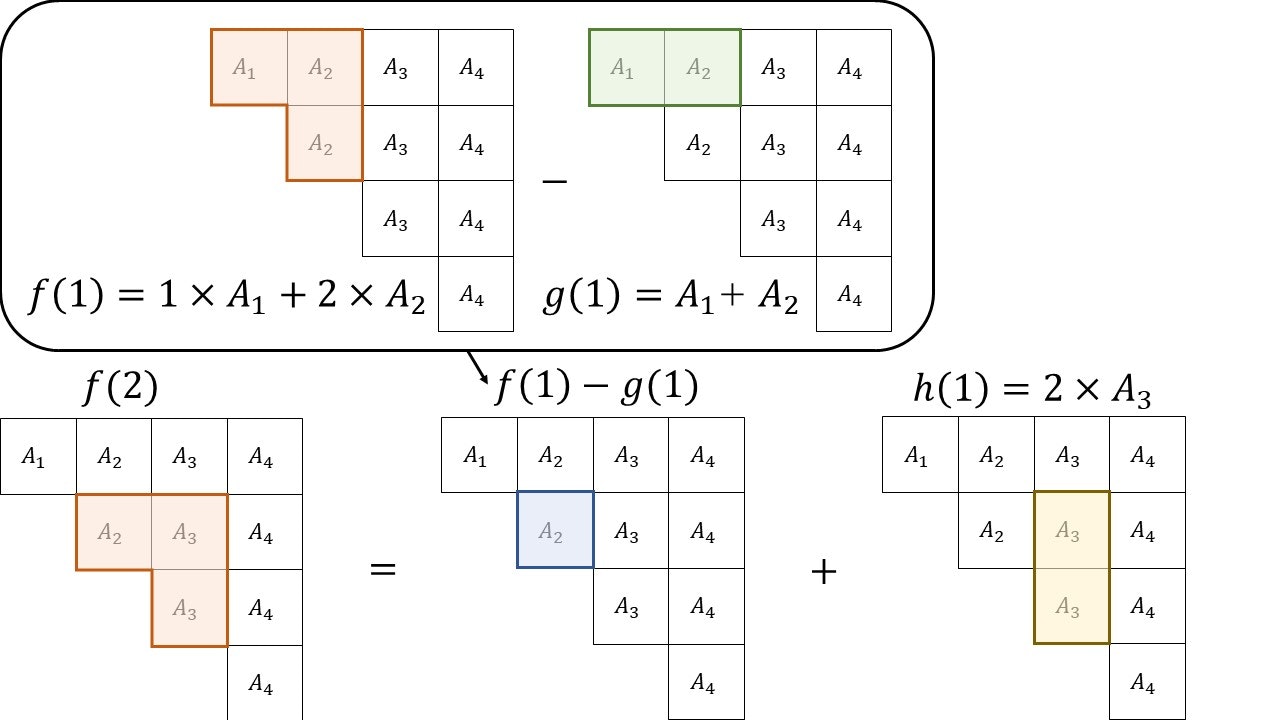
f(2)=f(1)-g(1)+h(1)\\
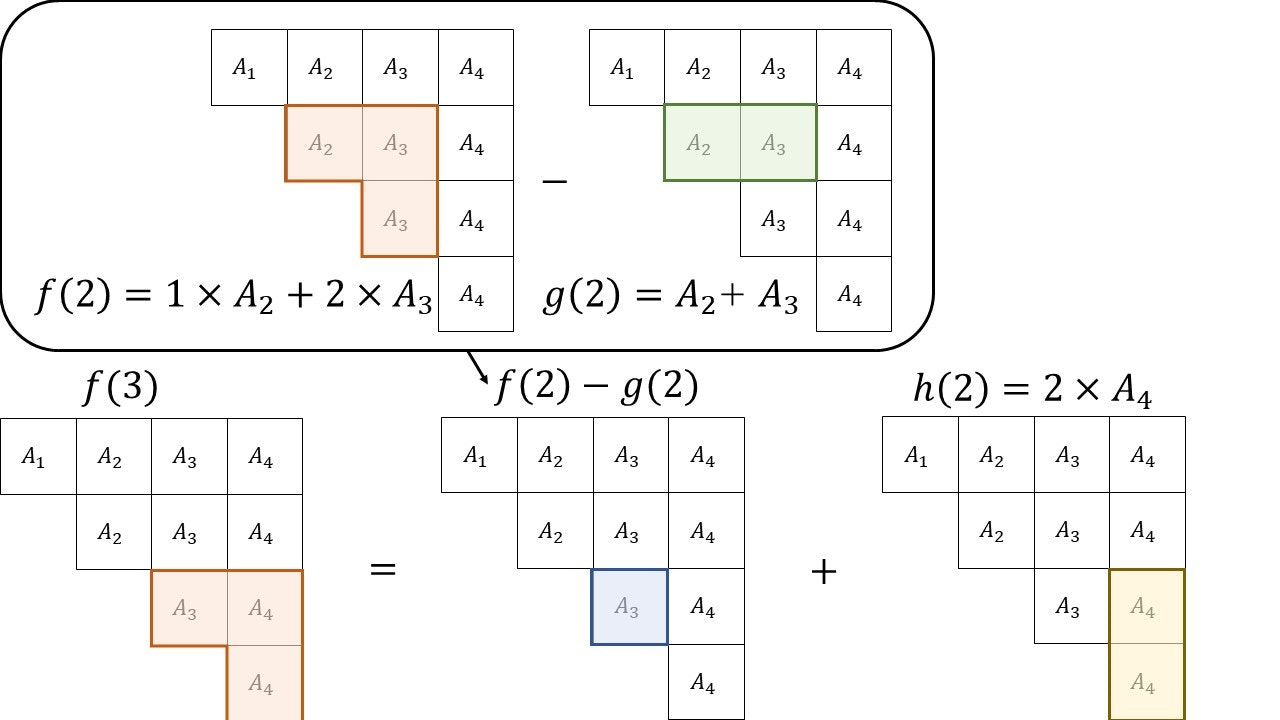
f(3)=f(2)-g(2)+h(2)\\
\vdots\\
f(x+1)=f(x)-g(x)+h(x)
式よりも図として見る方が理解しやすいと思います。
さらに
g(2)=g(1)-A_{1}+A_{1+M}\\
g(3)=g(2)-A_{2}+A_{2+M}\\
\vdots\\
g(x+1)=g(x)-A_{x-1}+A_{x+M}
より、$f(x),g(x)$は$f(1),g(1)$さえ求めれば以降は$O(1)$で求められることになります。
なお、$h(x)$はただの乗算なのでこちらも計算量は$O(1)$です。
したがって、最終的な計算量は
f(1)=O(M)\leq O(N)\\
g(1)=O(M)\leq O(N)\\
となります。