AtCoder Beginner Contest 152

###C - Low Elements

$P_{i}$は前すべて数より小さくなければならない。

import sys
n, *p = map(int, sys.stdin.read().split())
c = 0
minp = p[0]
for i in p:
    if i <= minp:
        c += 1
        minp = i
print(c)

###D - Handstand 2

解説をコードで実装する。

n = input()
intn = int(n)
ln = len(n)

if intn < 10:
    print(n)
    quit()


# 先頭の桁の数はiに等しく、末尾の桁の数はjに等しい整数kの数を取る
def count(i, j):
    res = 0
    if i == j:
        res += 1
    if ln == 2:  # 二桁の場合
        if 10 * i + j <= intn:
            res += 1
    else:
        res += (10**(ln - 2) - 1) // 9
        # 例えば、
        # nが三桁の場合、二桁のkが1つ
        # nが四桁の場合、二桁のkが1つ、三桁のkが10つで、合計11つ

        if i < int(n[0]):
            res += 10**(ln - 2)
            # i***j(*の数がln-2)のような形のkが全部とれる

        elif i == int(n[0]):  # n='iabcd'の場合
            tn = int(n[1:-1])  # 'iabcj'の'abc'をとる
            if j <= intn % 10:  # j<=d
                res += tn + 1  # 'i000j'~'iabcj'が全部とれる
            else:
                res += tn  # 'iabcj'がとれない
    return res


res = 0
for i in range(1, 10):
    for j in range(1, 10):
        res += count(i, j) * count(j, i)
print(res)

###E - Flatten

https://atcoder.jp/contests/abc152/submissions/9693323
を参考しました。
Aたちの最小公倍数をとってから、Aのモジュラ逆数をかけてBを求める。
一見すると最速解答だと思えないが、以下2つ関数を心得た。
min_factor:最小素因数を求める。
prime_factorize:素因数分解

import sys
read = sys.stdin.read

N, *A = map(int, read().split())
mod = 10 ** 9 + 7


def min_factor(n):
    sieve = list(range(n + 1))
    sieve[2::2] = [2] * (n // 2)
    for i in range(3, int(n ** 0.5) + 2, 2):
        if sieve[i] == i:
            sieve[i * i::2 * i] = [i] * ((n - i * i) // (2 * i) + 1)
    return sieve


table = min_factor(10**6)  # table[:10] = [0, 1, 2, 3, 2, 5, 2, 7, 2, 3]


def prime_factorize(n):
    a = {}
    while n != 1:
        b = table[n]
        if b in a:
            a[b] += 1
        else:
            a[b] = 1
        n //= b
    return a


# prime_factorize(18) = {2: 1, 3: 2}
# prime_factorize(39) = {3: 1, 13: 1}
dic = {}
for i in A:
    for key, value in prime_factorize(i).items():
        if key in dic:
            dic[key] = max(dic[key], value)
        else:
            dic[key] = value
# 最小公倍数を求める
lcm = 1
for i, j in dic.items():
    lcm *= pow(i, j, mod)
    lcm %= mod

answer = sum(lcm * pow(i, mod - 2, mod) for i in A) % mod
print(answer)

###F - Tree and Constraints
https://atcoder.jp/contests/abc152/submissions/9619555
を参考しました。
私にとってとても難しい。

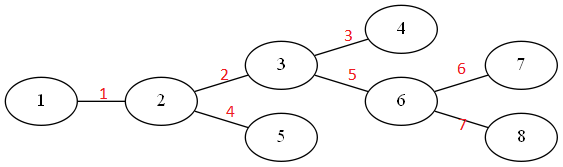
入力例4を例として挙げる。

8
1 2
2 3
4 3
2 5
6 3
6 7
8 6
5
2 7
3 5
1 6
2 8
7 8

入力中の木は以下のようなものです。

import numpy as np
import sys
readline = sys.stdin.readline

N = int(readline())
AB = list(list(map(int, readline().split())) for _ in range(N - 1))
M = int(readline())
UV = list(list(map(int, readline().split())) for _ in range(M))

graph = [[] for _ in range(N + 1)]
for i, (a, b) in enumerate(AB):
    graph[a].append((b, i))
    graph[b].append((a, i))



def get_path(U, V):
    INF = 100
    visited = [False] * (N + 1)
    pred = [None] * (N + 1)
    stack = [U]
    visited[U] = True
    while stack:
        v = stack.pop()
        for w, i in graph[v]:
            if visited[w]:
                continue
            visited[w] = True
            pred[w] = (v, i)
            stack.append(w)
    path = 0
    w = V
    while w != U:
        v, i = pred[w]
        w = v
        path += 1 << i
    return path


condition_path = [get_path(u, v) for u, v in UV]
# 2進数の形でuからvに到達するため使った橋を記録する
# 5ペアのuvのpathが、['0110010', '0001010', '0010011', '1010010', '1100000']です。
# '0110010'の意味は「2から7に到達するため2,5,6番目の橋を利用する」


# 2進数nの'1'を数える。popcnt(7)=3,popcnt(9)=1
def popcnt(n):
    c = (n & 0x5555555555555555) + ((n >> 1) & 0x5555555555555555)
    c = (c & 0x3333333333333333) + ((c >> 2) & 0x3333333333333333)
    c = (c & 0x0f0f0f0f0f0f0f0f) + ((c >> 4) & 0x0f0f0f0f0f0f0f0f)
    c = (c & 0x00ff00ff00ff00ff) + ((c >> 8) & 0x00ff00ff00ff00ff)
    c = (c & 0x0000ffff0000ffff) + ((c >> 16) & 0x0000ffff0000ffff)
    c = (c & 0x00000000ffffffff) + ((c >> 32) & 0x00000000ffffffff)
    return c


S = np.zeros(1 << M, np.int64)
sgn = np.ones(1 << M, np.int64)
for i in range(M):
    S[1 << i:1 << (i + 1)] = S[:1 << i] | condition_path[i]
    sgn[1 << i:1 << (i + 1)] = -sgn[:1 << i]

# 一応理解したが、どう説明すればいいか…

# i:制約の満足状況を2進数で表す。例えばi=31が「全部満たす」、i=17が「他の制約に関係なく、制約1,5を満たす」

# S[i]が「状況iで全部白く塗られればならない橋」です。
# S[0]が「すべての制約が不満足な時、全部白く塗られれば大丈夫」、
# i=0の時、S[1] = S[0]|condition_path1　⇒S[1]が「制約1を満足する時、2,5,6番目の橋が同時白くなれない」、
# i=1の時、S[2,3] = S[0,1]|condition_path2
#   ⇒S[2]が「制約2を満足する時、2,4番目の橋が同時白くなれない」
#   ⇒S[3]が「制約1,2を満足時、2,4,5,6番目の橋が同時白くなれない」、
# …

# sgnが集合の加減法のようなことをやっている。重複計算したら引き算で、引きすぎたらまた足し算。

n_edges = popcnt(S)  # 利用されている橋の数を計算
x = 1 << (N - 1 - n_edges)  # 各状況で「自由橋」の数により塗り方を計算
answer = (x * sgn).sum()

# sgn=[1 -1 -1 1 -1 1 1 -1 -1 1 1 -1 1 -1 -1 1 -1 1 1 -1 1 -1 -1 1 1 -1 -1 1 -1 1 1 -1]
# x = [128 16 32 8 16 8 8 4 16 8 8 4 8 4 4 2 32 88 4 4 4 2 2 8 8 4 4 4 4 2 2]
# すべての塗り方(x[0]=128)から、
# ①　制約1を満足する時、「1,3,4,7番目の橋に関わらず、2,5,6番目の橋が同時白く塗られる」の塗り方(x[1]=16)を引き、
# ②　制約2を満足する時、「1,3,5,6,7番目の橋に関わらず、2,4番目の橋が同時白く塗られる」の塗り方(x[2]=32)を引き、
# ③　でも、①②で「1,3,7番目の橋に関わらず、2,4,5,6番目の橋が同時白く塗られる」の塗り方(x[3]=8)を二回引いてしまった。
#    だからここでx[3]を足すべき。
# …

print(answer)