【競プロ】緑〜水のためのSegmentTree超入門

この記事について

SegmentTreeを「全く知らない」〜「聞いたことはある」くらいをイメージしながら書いています。

まあ、簡単なクエリ問題が解けるなら読めるんじゃないでしょうか。(しらんけど)

僕自身、つい数週間前にSegTreeを理解しただけなので、間違っているところがあればコメントお願いします...

参考にしたページ

https://qiita.com/ningenMe/items/bf66de877e3b97d35862
https://atcoder.github.io/ac-library/production/document_ja/segtree.html

セグ木とは?

皆さん大好きAtCoder Libraryを見てみます。

https://atcoder.github.io/ac-library/production/document_ja/segtree.html

何が書いてあるのかわかりません。丁寧にやっていきましょう。

---

まず次の問題を考えてみます。

長さNの数列A($A_0, A_1, \dots, A_{N-1}$)があります。はじめ、すべての要素は$2^{31}-1$です。
次の2種類のクエリが合計Q個与えられます。答えなさい。

• 0 i x : $A_i$をbに変更する。
• 1 s t : $A_s, A_{s+1}, \dots, A_t$の最小値を出力する。

制限:

• $1 \leq N \leq 10^5$
• $1 \leq Q \leq 10^5$
• 他はいい感じ

原作→ https://onlinejudge.u-aizu.ac.jp/courses/library/3/DSL/2/DSL_2_A

まず普通にやるとどうなるか考えてみます。
数列Aは$N\leq10^5$なので普通にそのまま変数として持っておきましょう。
クエリ0は、まあA[i] = xみたいにすれば当然$O(1)$です。

問題はクエリ1です。
範囲全てに対して一つ一つmin()を取っていくことを考えます。
このままだと、s=0, t=N-1の場合、$O(N)$です。
もしクエリが全て1だった場合、$O(N^2)$となり、間に合いません...

クエリの個数はどうしようもないので、当然クエリの処理時間を減らすことを考えます。
今回の場合、クエリ0($O(1)$)と比べてクエリ1($O(N)$)が異常に時間がかかっています。
なので、「クエリ0が少し遅くなってもいいからクエリ1を早くできるような方法」がほしいわけです。

ここで、クエリ0,1ともに$O(\log{N})$でできるという魔法のようなデータ構造が「Segment Tree」、略して「セグ木」なのです。

セグ木の構造

先程の問題を手で書いて考えてみます。
クエリ0,1がそれぞれ1:1くらいの比率で与えられるとすると、1要素を更新→1範囲の最小値計算、くらいになるわけです。
ここでやってみると、同じminの算出を何回も行っていることに気がつくと思います。1点が更新されただけなら、それを含まない範囲のminは変わらないわけです。

少し希望が見えてきました。つまり、部分的な結果を覚えておけば、それを流用して時間短縮ができそうです。

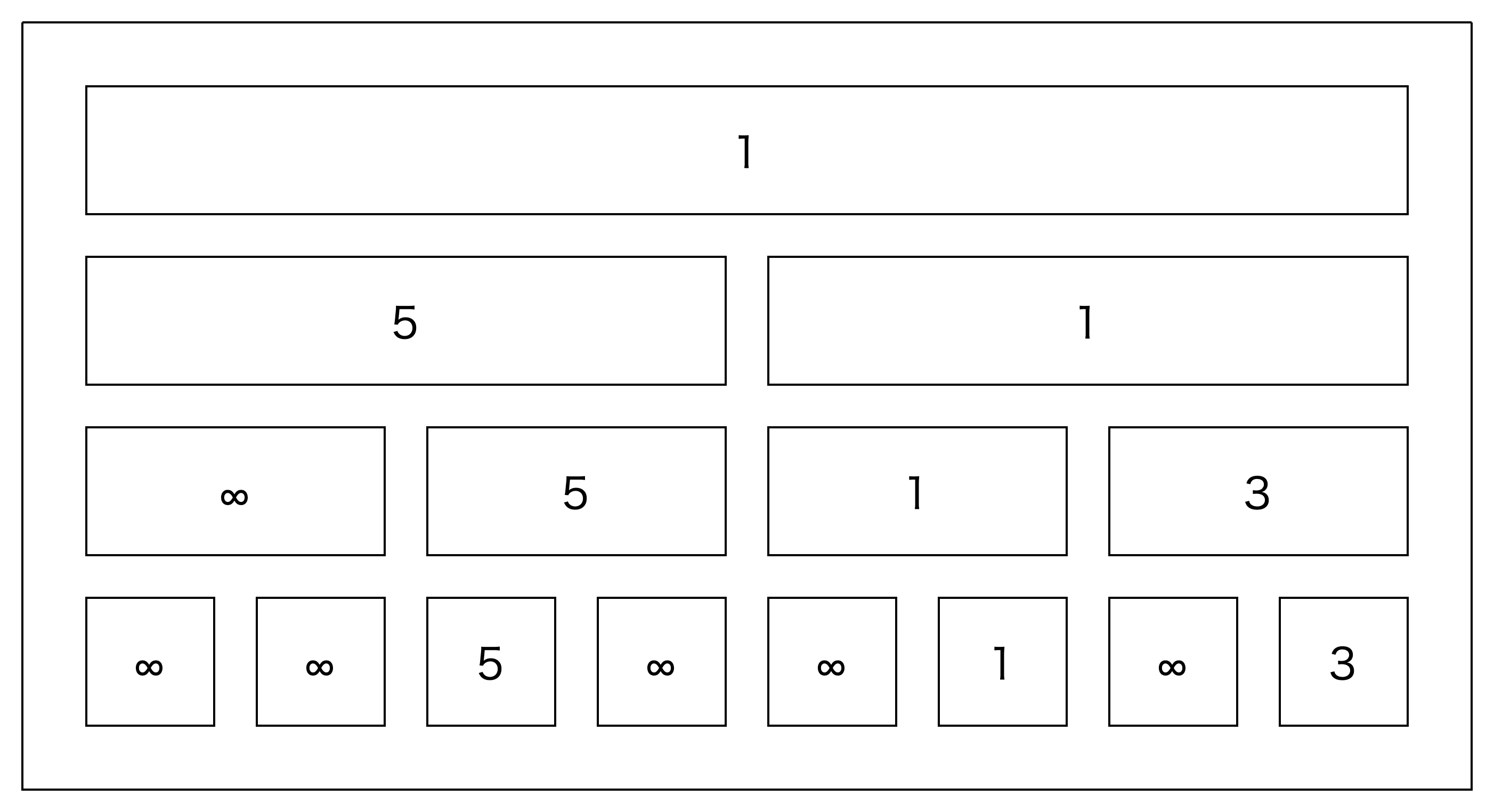
これを踏まえて次の図を見てください。これが、SegmentTreeの構造です。

図中のA[i~j]という表記は、(上の問題であれば)min(A[i], A[i+1], ..., A[j])をメモしている、と思ってください。
実際の値を最下層に置き、そこから上側にメモを置いている感じです。

これで本当に、「値の更新」「区間のminの算出」がともに爆速でできるのでしょうか?

やってみましょう。上の問題を解いてみます。
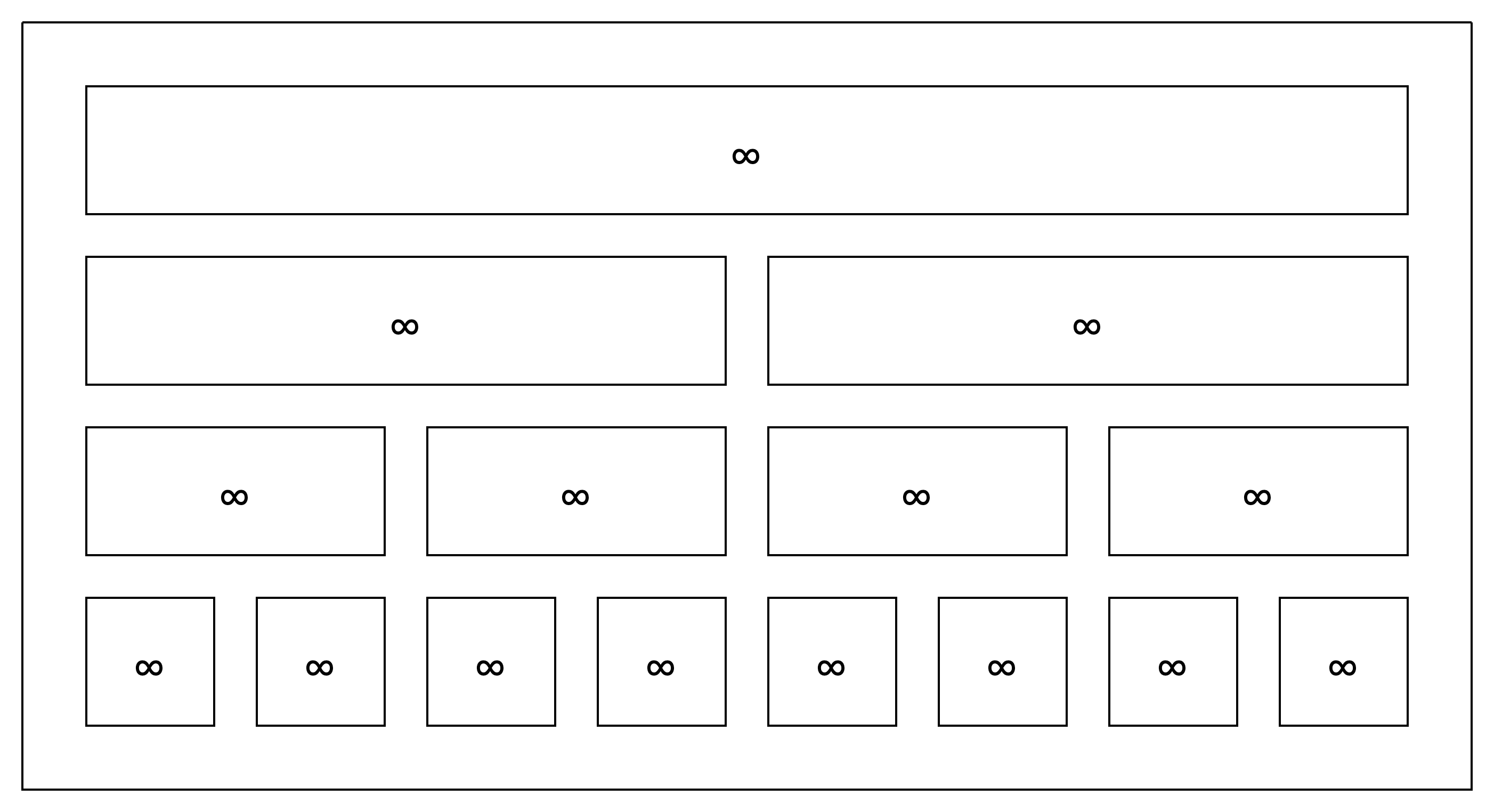
まず、Aのすべての要素は$2^{31}-1$だそうです。これは面倒くさいので、∞と表記します。

代入クエリの処理

まずは代入クエリだけを考えます。例えば以下。

0 2 5
0 5 1
0 7 3

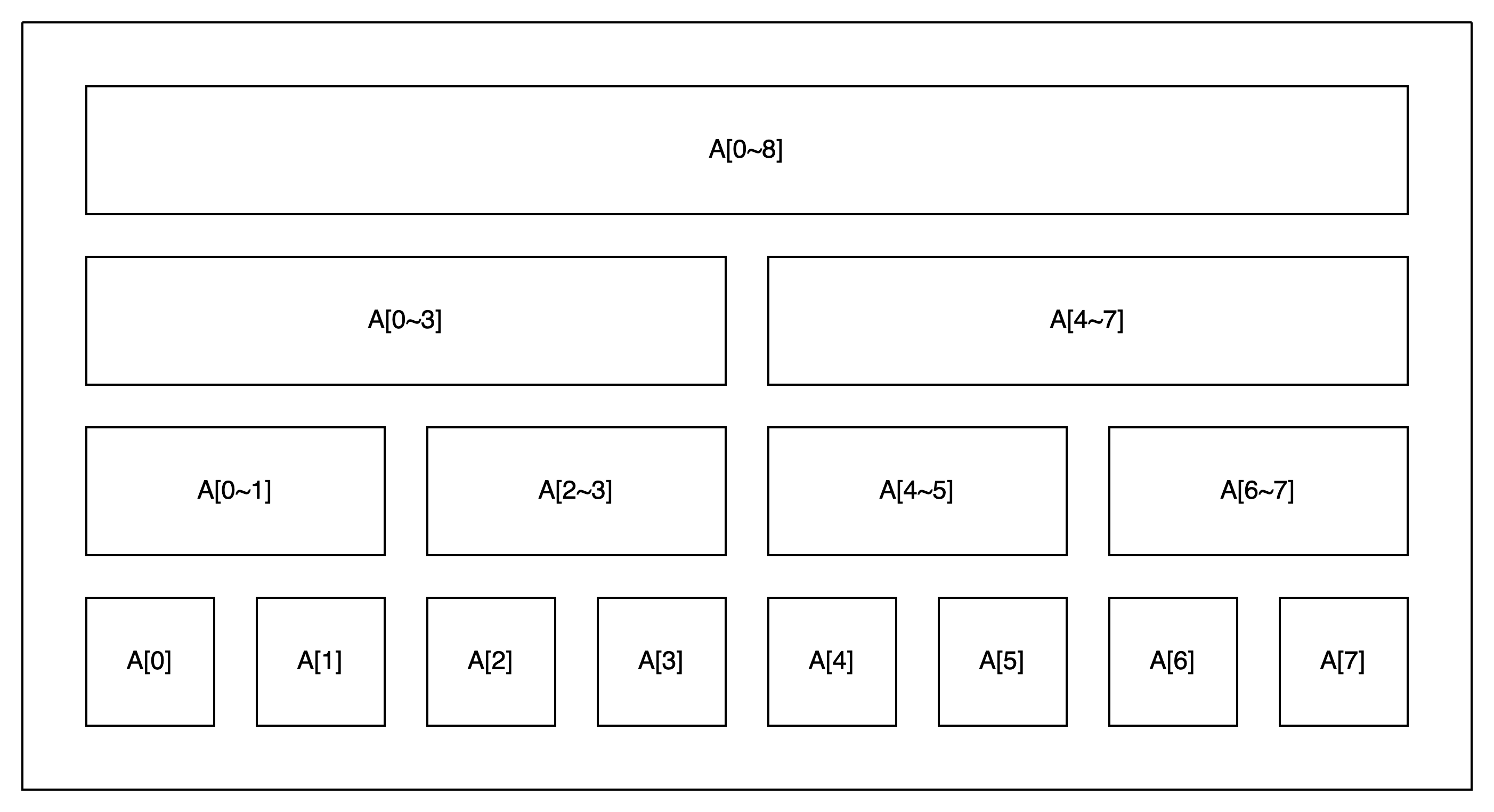
まずは1つめの「A[2]を5にする」クエリです。

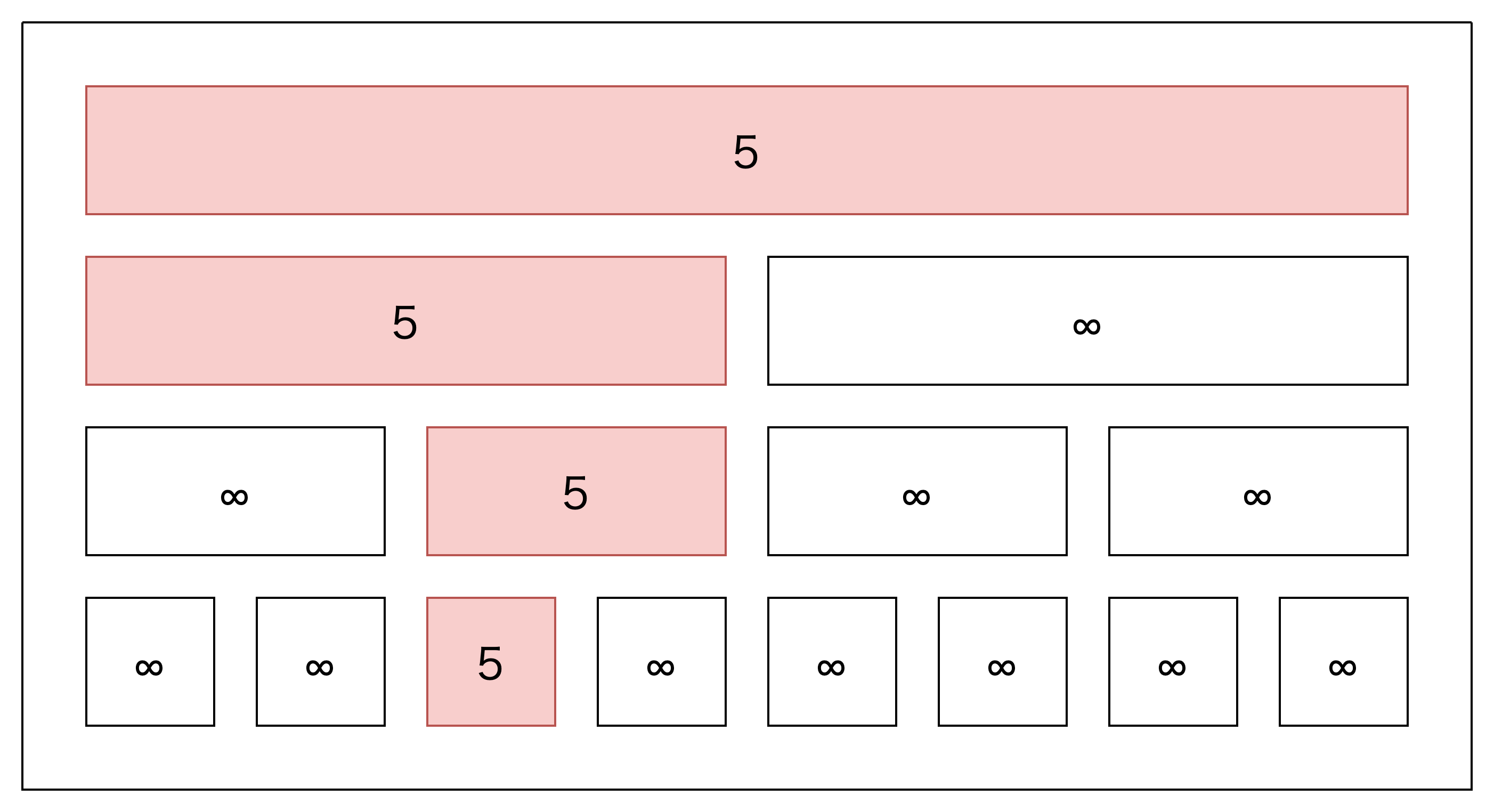
図に示された4つの赤色のマスが変化する事がわかりますか?
更新対象を含む範囲が変化する(可能性がある)わけです。
頂上の頂点を根として、下に伸びる木とみると、この構造は2分木と見ることができます。
この解釈で言えば、「更新された頂点(葉)から親をたどりながら更新していく」というわけです。
更新時は、「もとからある値」「新しい値」に対してmin()をすればよいです。

この調子で残り2クエリも処理していきましょう。

範囲計算クエリの処理

次に、区間minクエリの処理を考えます。

1 0 0
1 0 7
1 3 6

1つ目。0〜0の最小値...はA[0]ですね。
2つ目。0~7、つまり全範囲の最小値です。ところで、これは一番上のマスに書いてあるやつですね。1が答えです。
3つ目。3~6です。これを一つずつ探索するとすれば、全く高速化できていません。
なにかこのメモを使えるように変形してみましょう。
求めるものは下の赤いマスの最小値です。

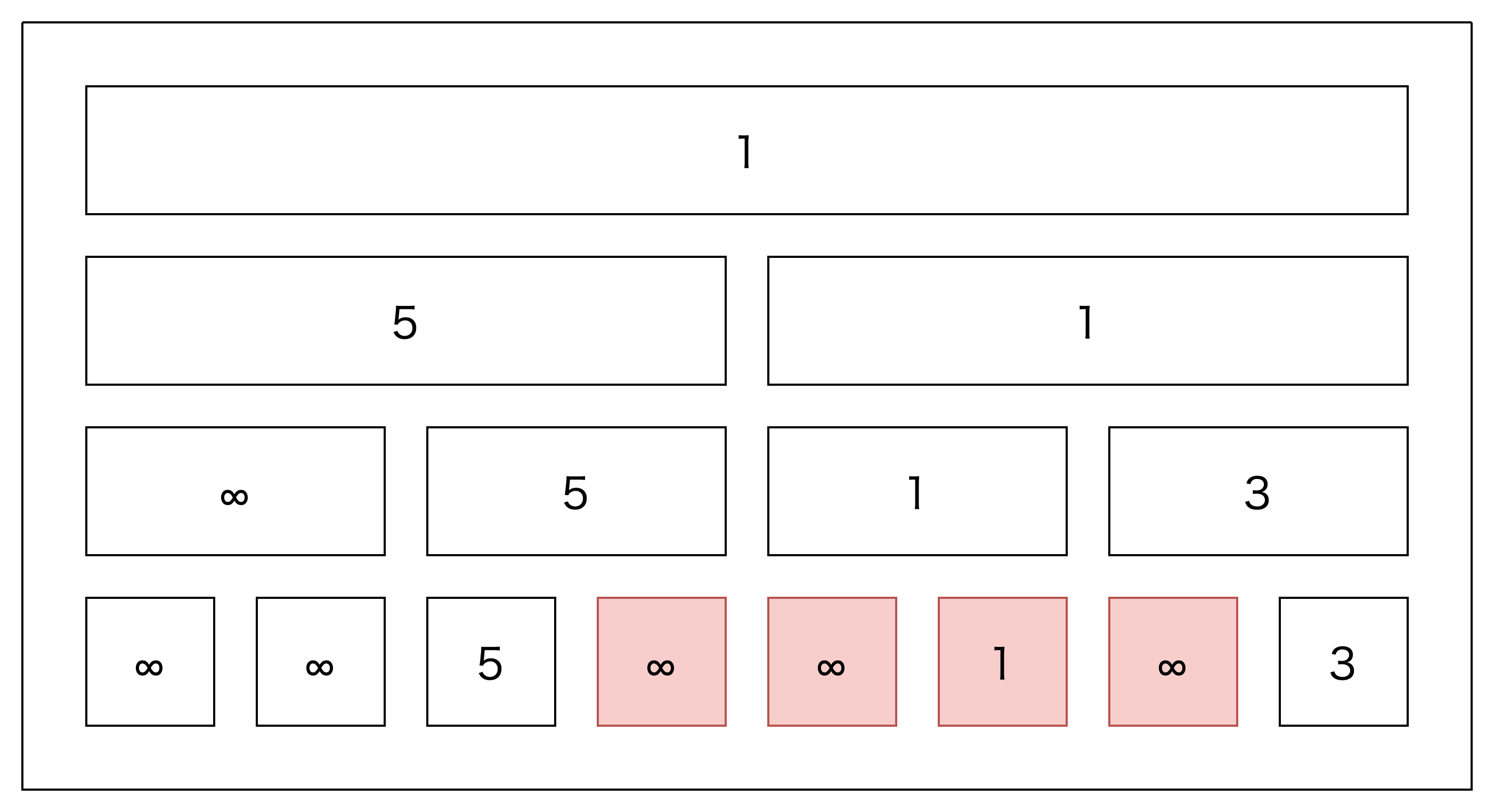
ところで、この4マスのうち、真ん中の2つの最小値って上のマスで計算されていますよね。
つまり、この3マスの最小値を求めればいいだけです。

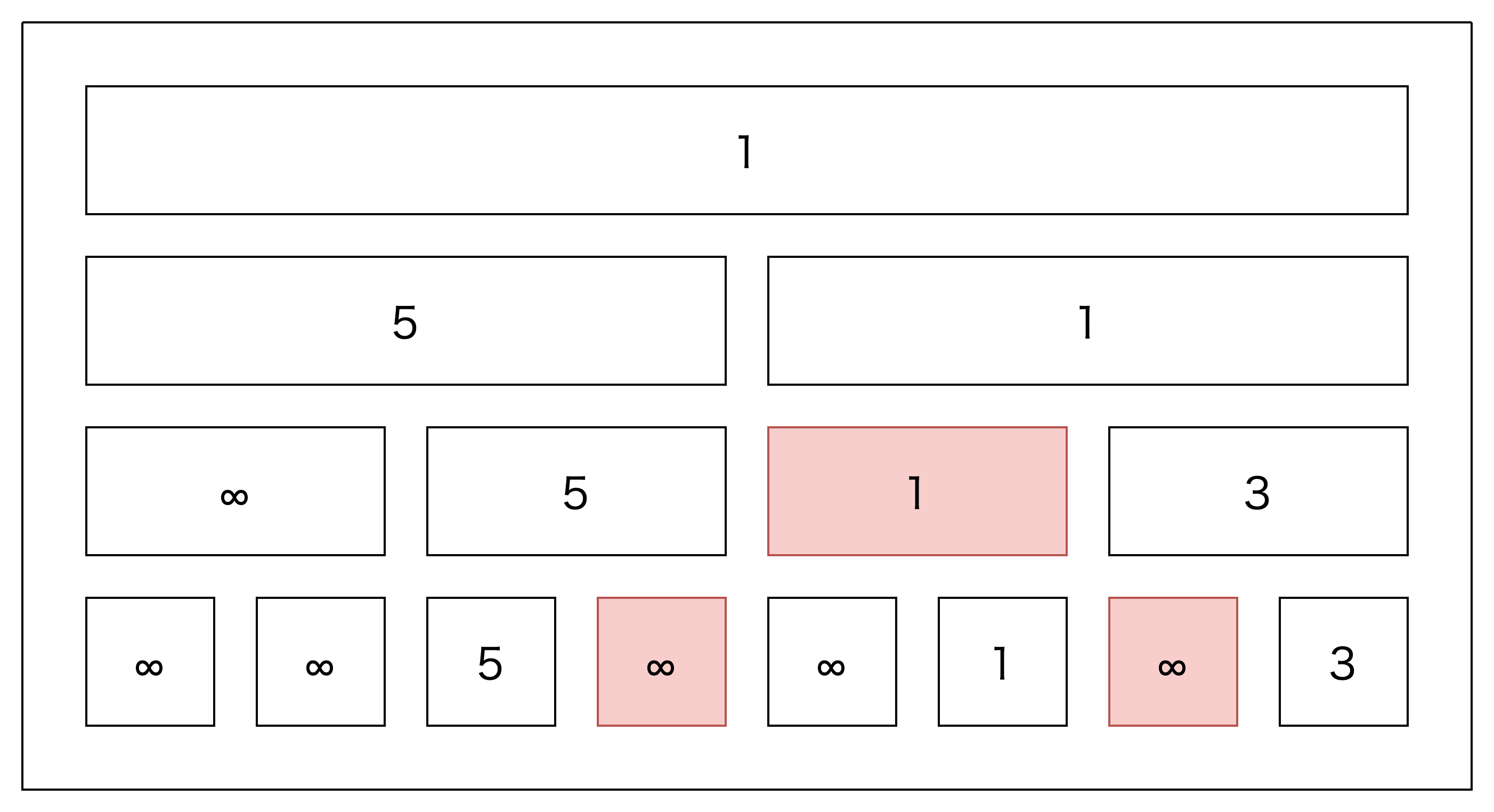
この場合は(規模が小さいので)4→3に減っただけであまり高速化していないように見えますが、1つ目や2つ目のクエリについても同じ考え方ができます。2つ目のクエリについては8→1となっており、かなり高速化できていますね。

これがそんなに早くなるのか? と疑問に思われる方もいると思いますが、実は最終的な赤いマスの数は$2\log{N}$程度に押さえることができます。
つまり、$O(N)$が$O(\log{N})$になったというわけです。めでたい。(定数倍の2は無視しています)

$2\log{N}$程度になることの証明もどき(超簡易版)

※ この証明は今考えたやつなので間違ってるかもです...

L~R、という範囲であるので、赤マスは(先程のように)山形に分布します。
ここで、左側(登り坂)の部分と右側(下り坂)の部分に分けて考えます。
(ただし、麓や頂上はめんどくさいので考えません。結果にはほぼ影響ないはず。)

左側だけを考えましょう。
この坂を構成するマスを一つ選んだとき、そのマスの横のマス(同じ層のとなりのマス)は赤いマスでないことを示します。
坂を構成するマス(のうち一つ)をマスA、その隣のマスをマスBとしましょう。

• AとBが同じ親を持っている場合、AやBではなくその親が選ばれ、赤マスとなるはずです。
• 逆に、AとBが異なる親を持っているが隣接する場合、(今考えているのは右上がりの領域のため)AとBのうち右側のマスは赤く塗られるはずがありません。なぜならば、右側のマスの親を塗ればよいからです。

これにより、「それぞれの坂について、マスは隣接しない」(階段で同じ高さの段は連続しない、段一つにつききちんと一つのマスが対応する)ことが示されました。
この木の高さは$\log_2{N}$です。そして、同じ高さの段には(左右で)せいぜい2つしか赤マスは存在しません。なので、赤マスの個数は最大でも$2\log{N}$くらいです。

これで、値変更クエリ、範囲演算クエリがともに$\log{N}$でできることがわかりました。これがSegment Treeです。

一般化

お察しの通り、セグ木はこれ以外の問題にも使うことができます。では、どのような場合に使えるのでしょう?

まず、A[i]に入るべき「値」、および、演算結果を出すための「演算」が必要です。ここで、A[i]の型をTとすると、演算は2つのTを受け取ってTを返すものでないといけません。
(今回の場合、Tはint、演算はmin()です。)

そして、セグ木の仕組み上、範囲を区切ってそこだけ先に計算しておくということが発生します。つまり、区間の全てに対して演算をすることはわかっていますが、その演算の順序は決まっていないわけです。
(注: ここでの順序は、前後の入れ替わりではなく、どこを先に計算するか、という意味です。)
なので、計算の順番が変わっても影響のない操作でなければいけません。

厳密には、(演算を仮に$\times$で表しますが) $a \times (b \times c) = (a \times b) \times c$、すなわち結合法則が成り立てば良いようです。

また、初期値として使うのですが、$a \times e = a$となるような存在(乗算なら1、minなら∞)が存在する必要があります。このようなeを「単位元」と呼びます。

このような、「型Tを持つ」「T a, bを受け取りTを返す関数を持つ」「その関数は結合法則が成り立つ」「単位元eが存在する」という条件を満たすような型Tと操作のペアを「モノイド」と呼びます。

モノイドであれば、セグ木を用いることができるらしいです。詳しいことはわかりません...

実装

ではこれを実装してみましょう。

一応、特定の問題のために作る、という感じではなく、どんな問題でも対応できるようにライブラリ的に作る、という方針で行きます。
そのため、struct(またはclass)の知識が多少必要です。暇になれば書こうかとも思いますが、そこらへんは適当にググってください...

まず、structの定義です。モノイドの値の型(A[i]の型)はテンプレートでもらっておきます。残りの必要そうな情報(先程のモノイドの定義で出てきたような情報)はコンストラクタでもらいます。
なお、function<T(T,T)>という、あまり馴染みのないコードがありますが、これは「関数という型」だと思ってください。引数が(T,T)で返り値がTです。ふつうにop(1,2)みたいに実行できます。

template <typename T>
struct SegmentTree {
  function<T(T,T)> op;
  T e;
  SegmentTree(int N, function<T(T,T)> op, T e) : op(op), e(e) {
    // TODO
  }
}

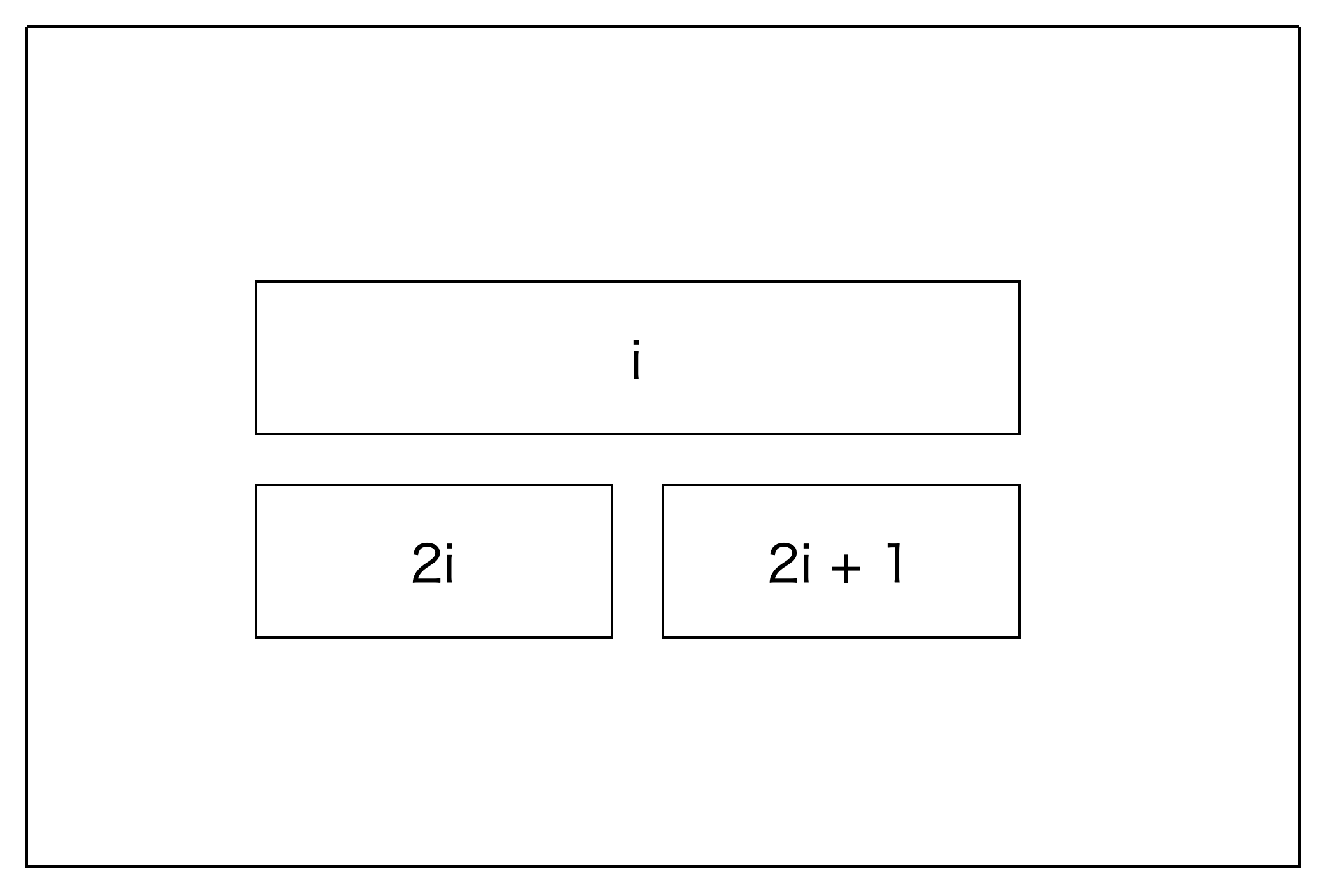
では、SegTreeの初期化をします。さっきの図のそれぞれのマスに、次のように番号を振りましょう。

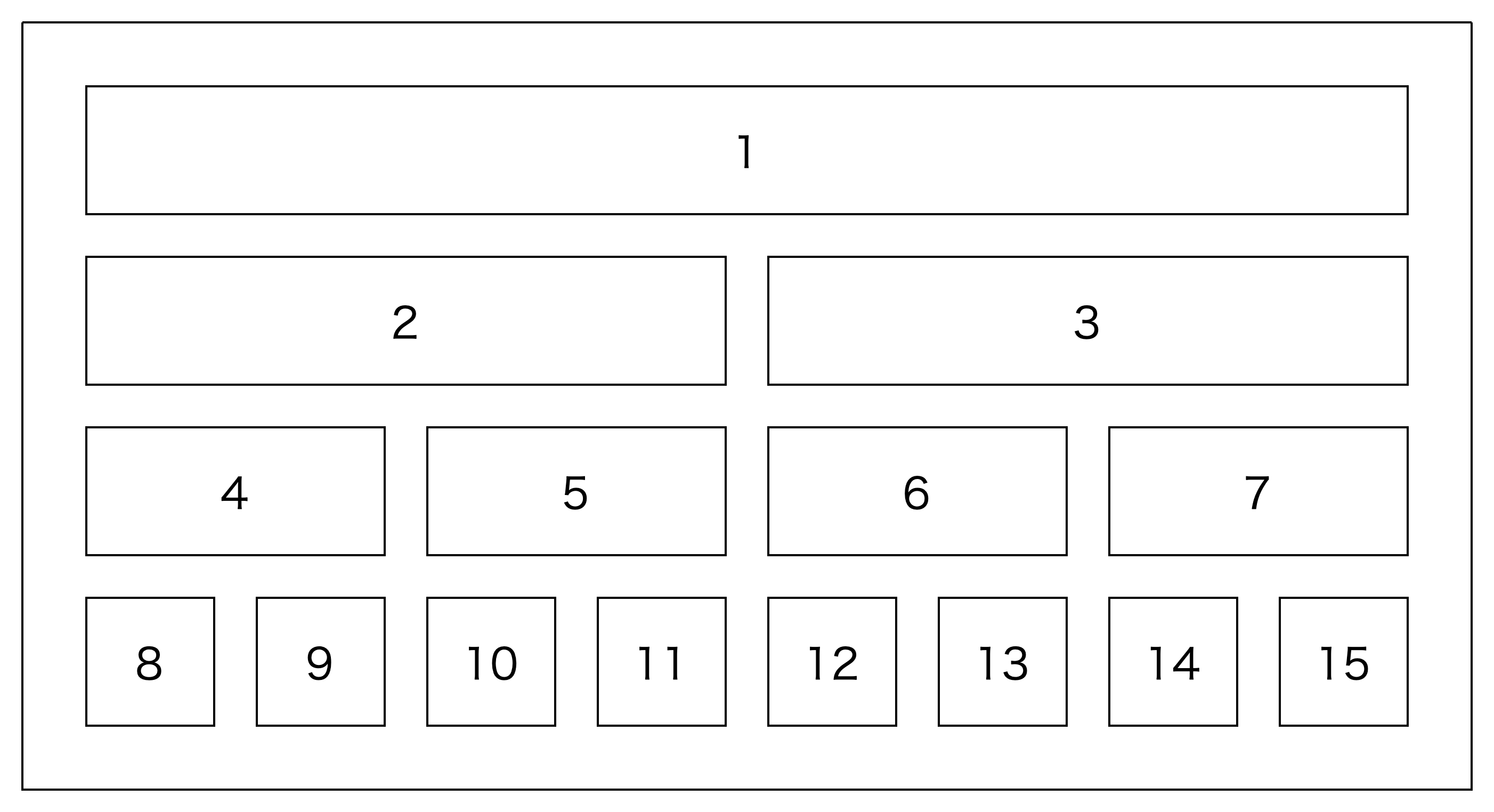
1始まりなのがポイントです。というのは、1始まりにすることで、「左の子=2倍」「右の子=2倍して1足す」となるのです。0始まりにしてしまうと少しややこしいです。

また、図をみると分かる通り、要素数は$2^k$の形であってほしいです。多分そうでなくとも動くのですが、実装がめんどくさくなります。なので、与えられたNをそのまま用いるのではなく、Nより大きい$2^k$を求め、それをnとして構築することにします。

マスの数はいくつでしょう? これは、$n=2^k$とすると、$1+2+4+\dots+2^k$です。
2進数で表してみましょう。$1+10+100+\dots+10000..00 = 111...111$(1がk個)までです。
これに1を足すと$2^{k+1}$となることから、マスの数が$2^{k+1}-1$であることがわかります。
今回、マスに設定した番号は、$1\sim2^{k+1}-1$です。これをそのまま配列のインデックスとして使いたいので、長さ$2^{k+1}$、すなわち2*nの配列を作り、[0]を使わないという運用をすることにします。

さて、SegTreeの内部配列(長さ2*n)が出てきたため、元々の配列(長さN)と混ざってややこしくなってしまいます。なので、内部配列の要素は「index=10」のように表し、元々の配列は「[10]」のように表すことにします。

では、ここまでを踏まえると、次のように実装できます。
はじめは全要素をeで初期化しておきましょう。

template <typename T>
struct SegmentTree {
  function<T(T,T)> op;
  T e;
  int n;
  vector<T> data;
  SegmentTree(int N, function<T(T,T)> op, T e) : op(op), e(e) {
    n = 1;
    while(n < N) n *= 2;
    data = vector<T>(2*n, e);
  }
}

要素更新

つぎに、要素更新の実装です。
「何に変更するか」と、「どこを変更するか」を受け取ります。
さっきいい感じにマスの番号を振ったため、index=xの親はindex=x/2となっています。(図を見てね)
奇数を割った場合は切り捨てになるのでいい感じになってくれるわけですね。

なので、根、すなわちx=1となるまで、親を遡りながら更新をしていけばよいです。
更新は、ノードの値を右の子(index=i*1)と左の子(index=i*2+1)をop()に放り込んだ値に更新するだけです。

ただし注意です。[i]に該当するはノードは最下層のやつなので、index=i+nに相当します。(図を見ましょう!)

template <typename T>
struct SegmentTree {
  // 略
  SegmentTree(int N, function<T(T,T)> op, T e) : op(op), e(e) {
    // 略
  }
  void set(int i, T val) {
    i += n;
    data[i] = val;
    while(i > 1) {
      i /= 2;
      data[i] = op(data[i*2], data[i*2+1]);
    }
  }
}

これで更新は完了です。

計算クエリ

次に、計算クエリを実装します。
範囲を与えられたら、その範囲すべてのop()の結果を返す、という関数です。なので、範囲を受け取りましょう。
半開区間[l, r)でもらうことにします。

つまり、「どこが赤マスになるか」を求めればいいわけです。
この図のような場合を考えましょう。

まず、範囲を[l, r)という半開区間で表現することにします。図の場合はl=1, r=6ですね。(0-indexです)

1段目(一番下の段)を考えます。今赤マスになりそうなものは、「9」と「13」です。

左端から考えましょう。9は赤マスにするべきでしょうか?
ここで、9は4の右の子供です。すなわち、9の祖先、つまり4,2,1あたりは、8~9の境目をうまく表現できません。
なので、9は選ばないといけません。「左端を考えるとき、自分が右の子ならば、赤マスに選ばれる」ことがわかりました。

右端を考えます。上と同様に考えると、13は選ばなくて良いですね。「右端を考えるとき、自分が右の子ならば、赤マスに選ばれない」ということです。

2段目に移ります。ただし、赤マスに登録した分、範囲を狭めておきます。
ここで候補は5,6ですね。5は先程と同様に、右の子であるため選ばれます。6は、これまた同様に考えて、「右端を考えるとき、自分が左の子ならば、赤マスに選ばれる」というわけで、選ばれます。

また範囲を狭めましょう。すると、左端と右端の線が一致しました。これで終了です。うまく赤いマスを取れていることがわかりますか?

ここからは実装について考えます。

このような、木の一部分のみを考えると楽でしょう。

右の子供であることは、自分のindexが奇数である、ということだと言いかえることができます。
また、親は(切り捨てで)自分のindexを2で割ればよいですね。

最後に、与えられる右端は開区間、つまりギリギリ含まれない場所だということを考慮しなければなりません。
「右端を考えるとき、自分が右の子ならば、赤マスに選ばれない」というのはつまり、「右端(開区間)を考えるとき、自分が左の子ならば、(自分-1は)選ばれない」ということです。
そして、「右端(開区間)を考えるとき、自分が右の子ならば、(自分-1は)選ばれる」ということにもなります。

これを踏まえて、実装です。

template <typename T>
struct SegmentTree {
  // 略
  SegmentTree(int N, function<T(T,T)> op, T e) : op(op), e(e) {
    // 略
  }
  void set(int i, T val) {
    // 略
  }
  T query(int l, int r) {
    l += n;                          // lに相当する位置の(SegTree上の)index
    r += n;                          // rも同様
    T l_val = e, r_val = e;          // l_val、r_valはそれぞれ、右/左のすでに赤く塗られたマス全てに対しop()した値」です
    while(l < r) {                   // 右端/左端が一致しない間
      if(l % 2 == 1) {               // lが右の子ならば
        l_val = op(l_val, data[l]);  // l_valの更新 (赤く塗る、に相当)
        l++;                         // lを右にずらす; いまlは右の子なので、別の親の下へと移動する
      }
      if(r % 2 == 1) {               // rが右の子ならば
        r--;                         // rを左にずらす; 今rは右の子なので親は変わらない。また、左にズレたことで、このrは範囲内の最も右の要素となる
        r_val = op(data[r], r_val);  // 現時点でのrを赤く塗る
      }
      l /= 2;                        // lを一段上に登らせる
      r /= 2;                        // rを一段上に登らせる
    }
    return op(l_val, r_val);         // 最終結果はこの2つのop()
  }
}

ややこしいですね...書いていて頭がおかしくなりそうです...

最終コード

これで一応完成です。

template <typename T>
struct SegmentTree {
  function<T(T,T)> op;
  T e;
  int n;
  vector<T> data;
  SegmentTree(int N, function<T(T,T)> op, T e) : op(op), e(e) {
    n = 1;
    while(n < N) n *= 2;
    data = vector<T>(2*n, e);
  }
  void set(int i, T val) {
    i += n;
    data[i] = val;
    while(i > 1) {
      i /= 2;
      data[i] = op(data[i*2], data[i*2+1]);
    }
  }
  T query(int l, int r) {
    l += n;
    r += n;
    T l_val = e, r_val = e;
    while(l < r) {
      if(l % 2 == 1) {
        l_val = op(l_val, data[l]);
        l++;
      }
      if(r % 2 == 1) {
        r--;
        r_val = op(data[r], r_val);
      }
      l /= 2;
      r /= 2;
    }
    return op(l_val, r_val);
  }
}

使い方はこんな感じ。(はじめに提示したDSL_2_Aです)

#include <bits/stdc++.h>

using namespace std;
#define rep(i, n) for(int i=0; i<n; i++)

template <typename T>
struct SegmentTree {
  // 略
};

int main() {
  int n, q;
  cin >> n >> q;
  SegmentTree<int> seg(n, [](int a, int b){return min(a, b);}, (1LL<<31)-1);
  rep(i, q) {
    int com, x, y;
    cin >> com >> x >> y;
    if(com == 0) {
      seg.set(x, y);
    } else if(com == 1) {
      cout << seg.query(x, y+1) << endl;
    }
  }
}

まとめ

Segment Treeのお話でした。query()のところとか難しすぎて説明グチャクチャなんですが...(再帰関数を使った、もっと簡単な実装もあります。暇があれば書きますが...)

ただし、SegmentTreeを用いれば、一見無理なクエリ問題を簡単に解くことができます。結構楽しいです。といっても僕はまだ実践利用したこと無いんですけどね。

実践的に言えば、(自分で実装せずとも)AtCoder Libraryを使えればそれで十分です。ただし、中身をちらっと知っておくと応用が効くので、損はないと思います。

あと、LazySegmentTreeというものもあります。これは、イメージでいえば、set()を区間で行えるようにしたようなものです。多分。これもいつか書こうと思っていますが、まあまあ難しいので分量が大変なことになるのではないかと危惧しています...