Revitモデルから警備員の巡回路を求める

はじめに

DANSO（建築情報学会） Advent Calendar 2022 の13日目の記事です。
この記事は12日目の記事の続編です。

前回 NetworkX でつくったグラフマップを使って巡回セールスマン問題を解きます。

本記事では巡回セールスマン問題を解くアルゴリズム中身については詳しく解説せず、実装方法のみ紹介します。

最短の巡回路を求めたい

大学を巡回する警備員はエレベーターホールから出発し、フロアの研究室・教室を1回だけ訪れてエレベーターホールに戻ります。この条件を満たす巡回路において、警備員が歩く距離（経路コスト）が最小のものを求めます。

この問題は 巡回セールスマン問題（TSP：Traveling Salesman Problem） の類似問題として解決することができます。TSPとは、$V$ 頂点からなる重み付き完全グラフについて、全ての頂点をちょうど一度ずつ巡り出発地に戻る巡回路のうち、総移動コスト（重みの合計）が最小のものを求める組合せ最適化問題です。TSPの解法は最適化分野で古くから研究されており、集積回路の設計や運送会社の配送計画などに応用されています。

TPSの解法は様々な手法が提案されていますが、大きく分けて以下の2つに分類されます。

• 厳密解法：厳密解を求める解法です。$V$ が大きくなると計算量が急増するため実用的ではありません。
• 近似解法：精度がある程度よい近似解を求める解法です。$V$ がある程度大きくても高速に解を求めることができます。

計算用の完全グラフをつくる

前回扱ったグラフマップは、機械室や廊下など巡回する必要のない部屋が頂点に含まれています。またグラフマップは完全グラフではないため、TSPのモデルをそのまま適用することはできません。そこでグラフマップから不要な頂点を取り除き、さらに残りの頂点間のパスを再計算することで、計算用の完全グラフをつくります。

グラフマップをロードする

前回と同様にしてJSONファイルからグラフマップを復元します。

pythonスクリプト

import json
import networkx as nx

def read_json_file(path):
    with open(path, "r", encoding="utf-8") as json_file:
        json_data = json.load(json_file)
    return nx.readwrite.json_graph.node_link_graph(json_data)
    
graph = read_json_file(<ファイルパス>)

グラフを描画します。$115$ 頂点、$1030$ 辺からなるグラフです。

グラフマップを完全グラフに変換する

nx.Graph()で新しく無向グラフをつくり、グラフマップの各頂点の中で名前が「部屋○○」「教室○○」「エレベーターホール」のものをadd_nodes()で追加します。
次にnx.dijkstra_path() nx.dijkstra_path_length()で追加された頂点間の最短経路とその距離を取得します。add_edge()で頂点間の辺をつくり、最短経路と距離を辺にタグ付けします。

pythonスクリプト

from itertools import combinations

def get_complete_graph(graph):
    complete_graph = nx.Graph()
    # node
    for node, tag in graph.nodes(data=True):
        if node[:2] in ("部屋", "教室"): complete_graph.add_node(node, x=tag["x"], y=tag["y"])
    # edge
    for node1, node2 in combinations(complete_graph.nodes, 2):
        path = nx.dijkstra_path(graph, node1, node2)
        length = nx.dijkstra_path_length(graph, node1, node2)
        complete_graph.add_edge(node1, node2, weight=length, path=path)
    return complete_graph

complete_graph = get_complete_graph(graph)

$V_{1}$ 頂点、$E_{1}$ 辺からなるグラフマップを $V_{2}$ 頂点からなる完全グラフに変換するとき、計算量は $O(V_{2}^2 E_{1} logV_{1})$ となるため短時間で実行できることが分かります。

グラフを描画します。$23$ 頂点からなる完全グラフで、各辺に最短経路がタグ付けされていることが分かります。

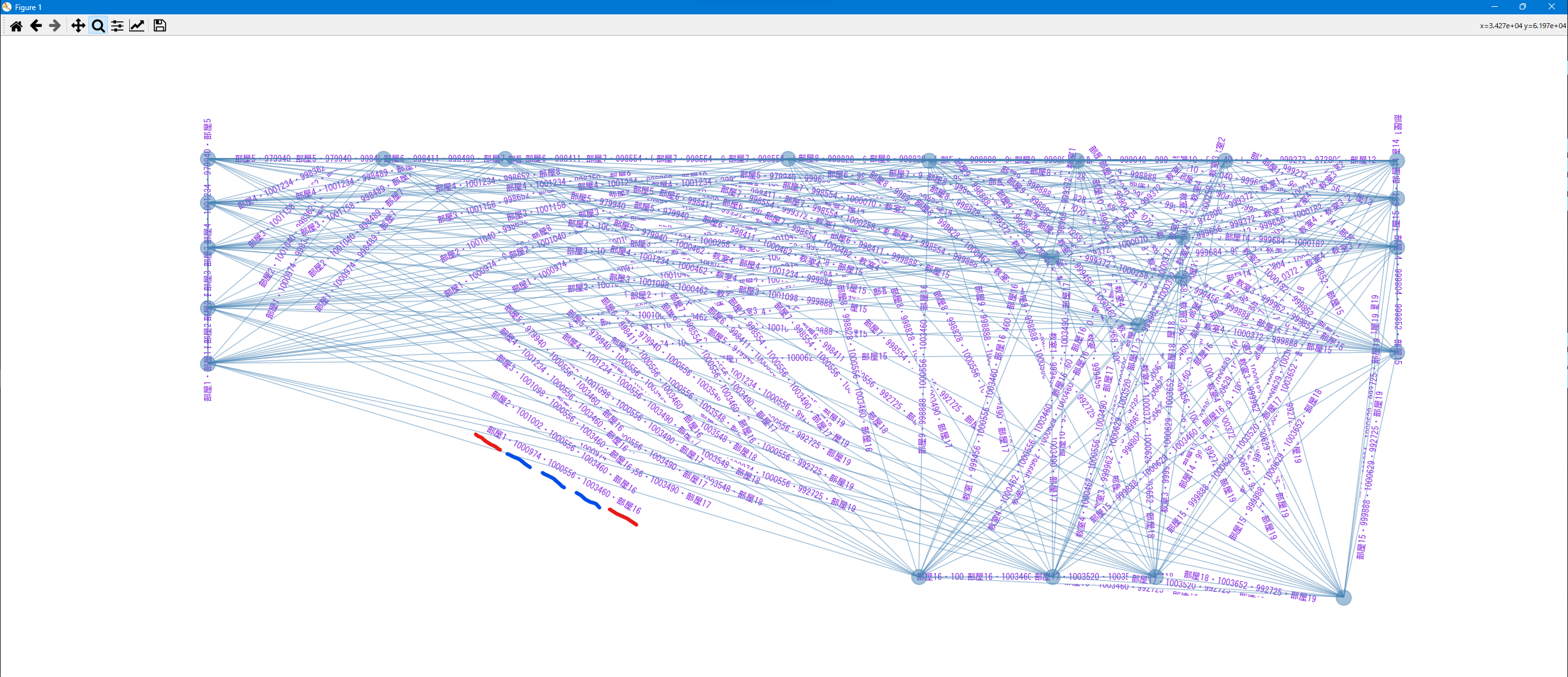
遺伝的アルゴリズムで巡回路を求める

はじめに述べたように、TSPの厳密解法はグラフの頂点数が増加すると計算量が急増してしまいます。例えば $V=30$ の場合、巡回路の組み合わせは $4.42×10^{30}$ 通りとなり、これをすべて計算するのは現実的ではありません。そのため現実的な時間で近似解を求められるアルゴリズムを用います。TSPやその他多くの最適化問題で用いられる近似アルゴリズムとして、以下のようなものがあげられます。

• ランダムサーチ
• 山登り法
• 焼きなまし法
• 遺伝的アルゴリズム

今回は以下の記事を参考にして、遺伝的アルゴリズム（GA:Genetic Algorithm） でTPSの解を求めます。※目的関数など記事と異なる箇所もあります

GAは生物の遺伝子の進化を模したアルゴリズムです。部屋の訪問順の並びを生物個体の遺伝子に見立て、同世代の個体の中で「選択」「突然変異」「交叉」と呼ばれる操作を行って次世代を生み出すことを繰り返し、最適解を探索します。GAは最適化問題の解法としては応用性が高く、多峰性の問題にも強という特徴があります。

SimpleAIとは

SimpleAI はお手軽に探索アルゴリズムを実装できる Pythonパッケージです。

pythonスクリプト

import random, copy
from simpleai.search import SearchProblem
from simpleai.search.local import genetic

個体の遺伝子を定義する

以下のようなルールで巡回路から個体の遺伝子（数列）を求めます。

graph.nodes()で頂点リストを求め、巡回路の全ての頂点について以下の操作を繰り返します。

1. 巡回路の $i$ 番目の頂点 $V_{i}$ が、頂点リストの中で $j$ 番目にあるとき、遺伝子の $i$ 番目の染色体を $j$ とする
2. 頂点リストから頂点 $V_{i}$を取り除く

例えば[A,B,C,D] = graph.nodes()のとき、巡回路[A,D,C,B]から個体0,2,1,0が求まります。

個体から巡回路を生成する関数を定義します。

pythonスクリプト

def gene_2_route(gene):
    destinations = list(copy.deepcopy(complete_graph.nodes))
    route = []
    for index in gene:
        node = destinations[index]
        destinations.pop(index)
        route.append(node)
    route.append(route[0])
    return route

GAを実装する

Simple AI のSearchProblemクラスを継承してTSPGAクラスをつくり、value()　generate_random_state() crossover() mutate()の4つのメソッドをオーバーライドします。

「選択」value()
個体から巡回路を求めて経路コストを計算し、より低コストな個体を選ぶ操作です。

「初期値生成」generate_random_state()
個体の初期値をランダムに生成する操作です。

「交叉」crossover()
２つの個体がもつ遺伝子の染色体をそれぞれ $1/2$ の確率で取り入れ新しい個体を生み出す操作です。

「突然変異」mutate()
個体の遺伝子をランダムな位置で変更し、新しい個体を生み出す操作です。

pythonスクリプト

class TSPGA(SearchProblem):

    def value(self, state):
        # 選択
        route = gene_2_route(state)
        cost = -nx.path_weight(complete_graph, route, weight="weight")
        global max_state
        global max_cost
        if max_cost < cost:
            max_state = state
            max_cost = cost
        return cost
        
    def generate_random_state(self):
        # 初期値生成
        destinations = list(copy.deepcopy(complete_graph.nodes))
        gene = []
        for i in range(len(destinations)):
            node = random.choice(destinations)
            index = destinations.index(node)
            destinations.pop(index)
            gene.append(index)
        return gene

    def crossover(self, state1, state2):
        # 一様交叉
        child = []
        for i in range(len(state1)):
            p = random.random()
            if p < 0.5: child.append(state1[i])
            else: child.append(state2[i])
        return child

    def mutate(self, state):
        # 突然変異
        child = list(copy.deepcopy(state))
        index = np.random.randint(0, len(child))
        max = len(child) - index
        child[index] = np.random.randint(0, max)
        return child

GAを実行する

以下のようにパラメータを設定しGAを実行します。

• 1世代の数：1000
• 突然変異の確立：0.4
• 世代交代：5000

pythonスクリプト

initial_gene = [0]*complete_graph.number_of_nodes()
max_state = initial_gene
max_cost = -10**8
problem = TSPGA(initial_state=initial_gene)
result = genetic(problem, population_size=1000, mutation_chance=0.4, iterations_limit=5000)
route = gene_2_route(result.state)

求めた巡回路とグラフを描画します。経路コストは462294（＝警備員が歩く距離は約462m）となりました。

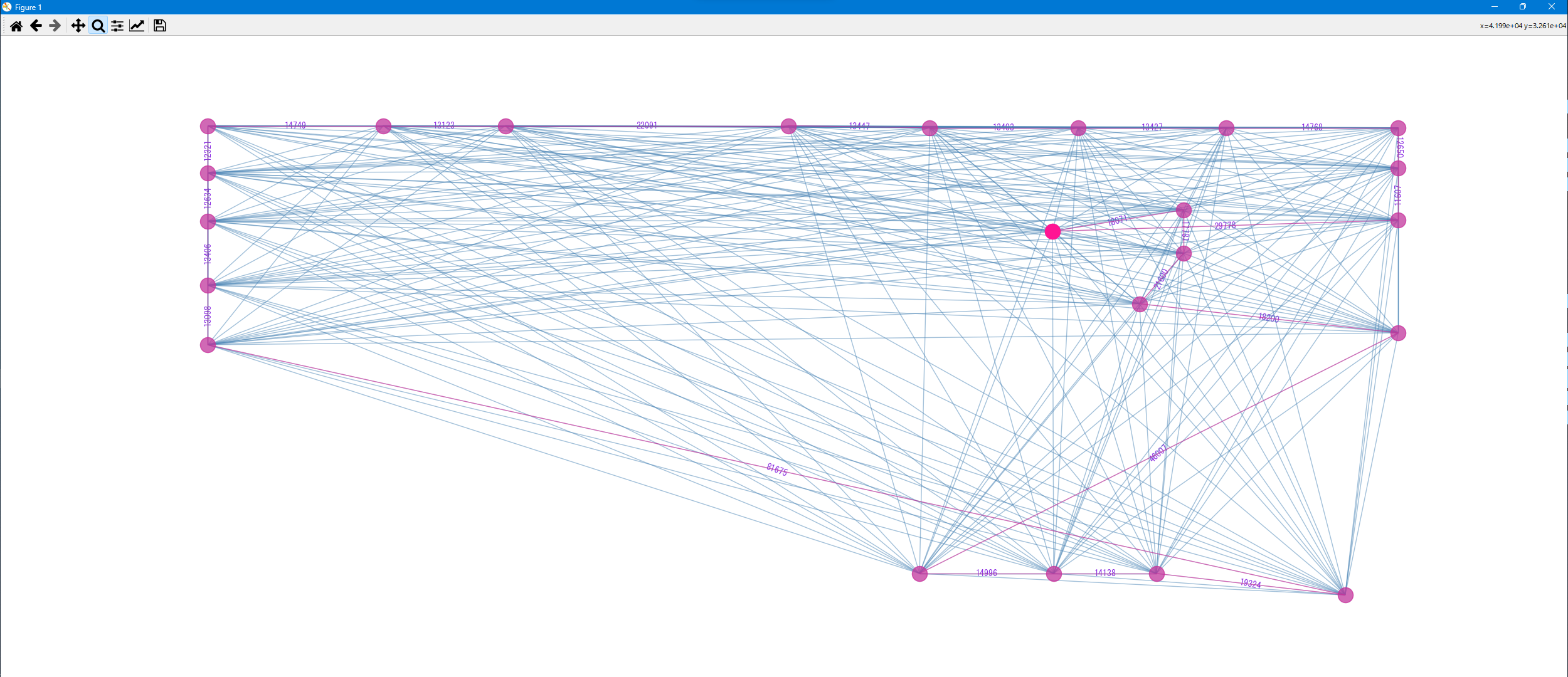
巡回路をグラフマップに反映する

完全グラフで求めた巡回路を使って、もとのグラフマップでの巡回路も求めます。完全グラフの各辺には最短経路がタグ付けされているので、その情報からグラフマップでの巡回路の各辺が分かります。

pythonスクリプト

def get_edges(route, complete_graph):
    edges = []
    route_edges = set(zip(route, route[1:]))
    for i, j, tag in complete_graph.edges(data=True):
        if (i, j) in route_edges or (j, i) in route_edges:
            path = tag["path"]
            edges.extend(set(zip(path, path[1:])))
    return edges

route_edges = get_edges(route, complete_graph)

巡回路とグラフを描画します。一部の辺が重なっているため分かりにくいですが、最短巡回路に近いルートを求められています。

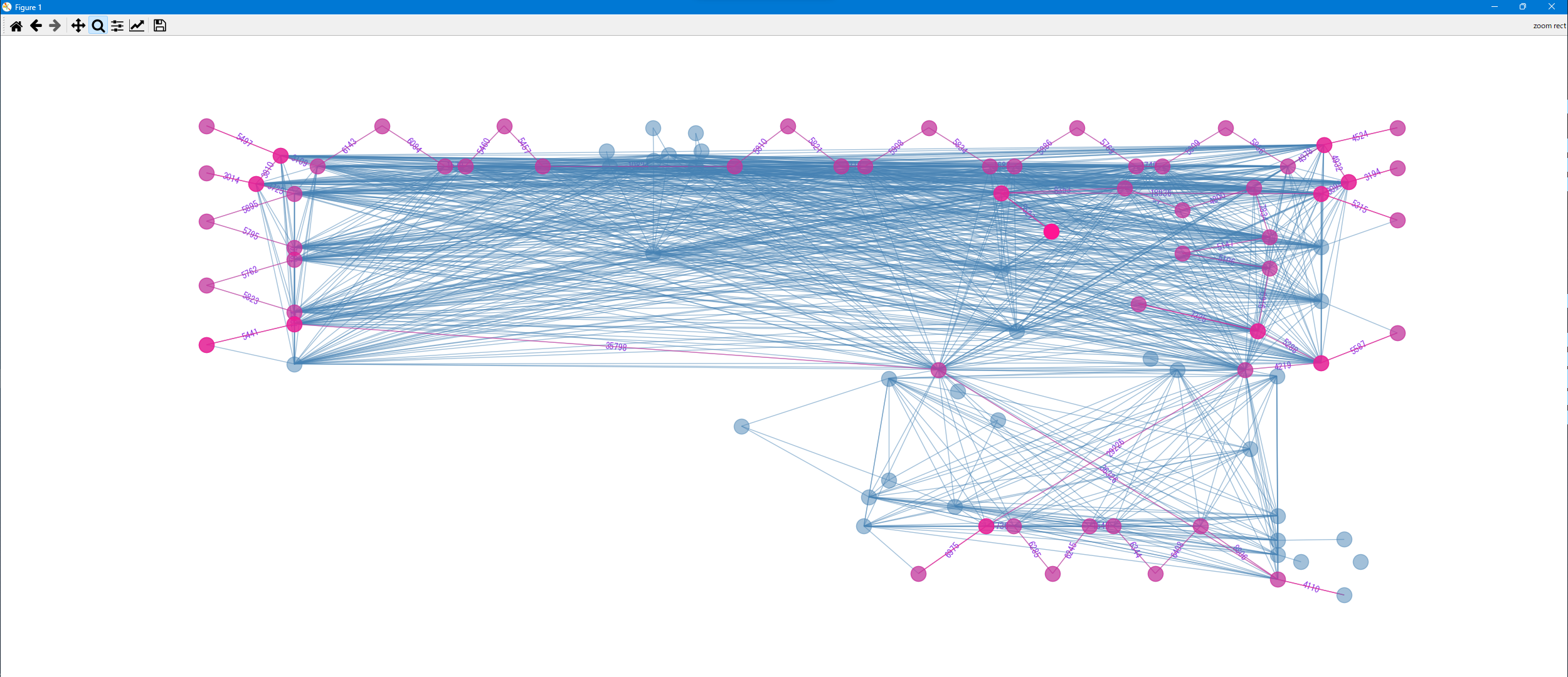
参考リンク