Revitモデルから部屋間の最短経路を求める

はじめに

DANSO（建築情報学会） Advent Calendar 2022 の12日目の記事です。
Dynamo と NetworkX を使ってRevitモデルの2部屋間の最短経路を求めます。

本記事ではRevit2022を使用しています。また、AnacondaでDynamo用の環境を用意しています。

環境
Revit 2022
Dynamo 2.12
Python 3.8.3

2点間の距離を求める

Revit APIには2点間の距離を求める PathOfTravel という機能が標準搭載されています。 DynamoではPathOfTravel.ByFloorPlanPointsノードを使って2点間の距離を求めることができます。

PathOfTravel は平面図を20cm×20cmのグリッドとして捉え、始点座標から終点座標までの最短経路をA*アルゴリズムで探索する仕組みになっています。そのため引数として平面図のviewを指定する必要があります。

pythonスクリプト

# dynamoノード
clr.AddReference("RevitNodes")
from Revit import Application
from Revit import Elements

def get_length(elem1, elem2):
    view = Application.Document.Current.ActiveView
    path = Elements.PathOfTravel.ByFloorPlanPoints(view, [elem1.Location], [elem2.Location], False)
    distance = int(path[0].GetParameterValueByName("長さ"))
    return distance

OUT = get_length(IN[0], IN[1])

実行すると移動経路インスタンスが作成されます。移動経路インスタンスは長さや移動時間などのパラメータを持っています。

NetworkXでグラフマップをつくる

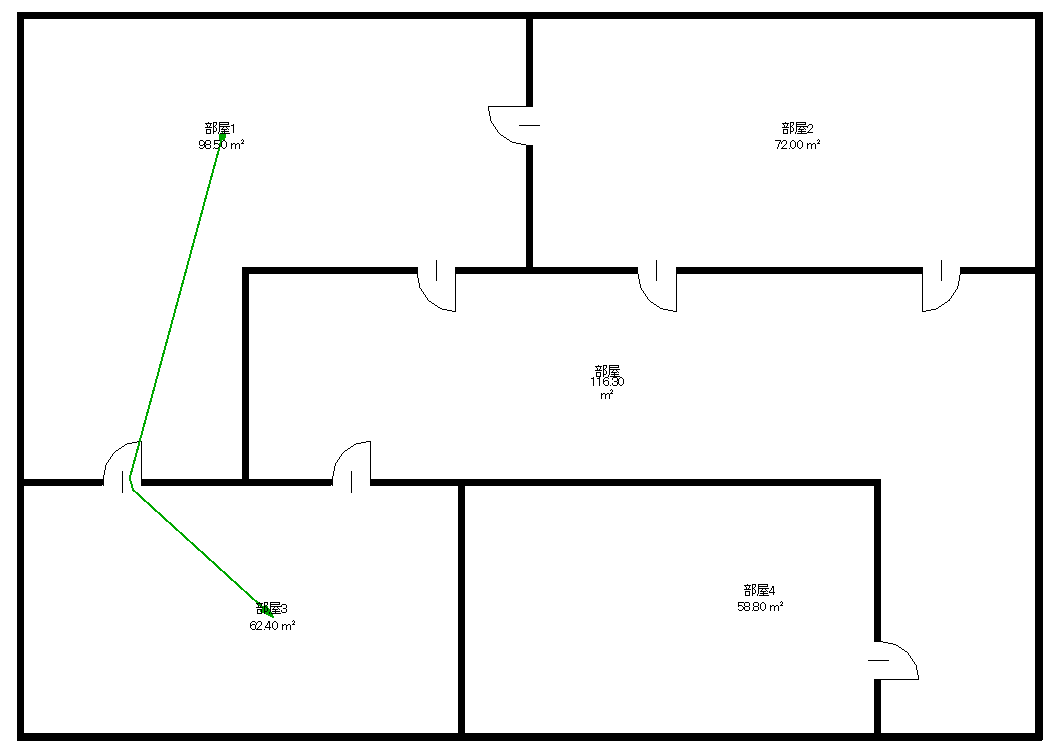
PathOfTravel で2部屋間の最短経路を求める場合、経路途中の部屋を取得できない、計算効率が悪い、経路計算にRevit・Dynamoが必要、などの問題があります。そこで各部屋の位置関係をグラフ構造で表現した グラフマップ に距離を記録することにします。ドアと部屋を頂点、部屋⇔ドア間とドア⇔ドア間の最短経路を辺とした単純無向グラフをつくり、辺の距離を重みとして各辺に与えます。

NetworkXとは

NetworkX はグラフ/ネットワーク理論系の計算を行うためのPythonパッケージです。NetworkX を使用するとネットワーク分析、ネットワーク構造の可視化、中心性や連結性などの解析、　最短経路計算などを行うことができます。

NetworkXでグラフをつくる

Dynamoで部屋とそれに属するドアを取得し、Pythonスクリプトに入力します。

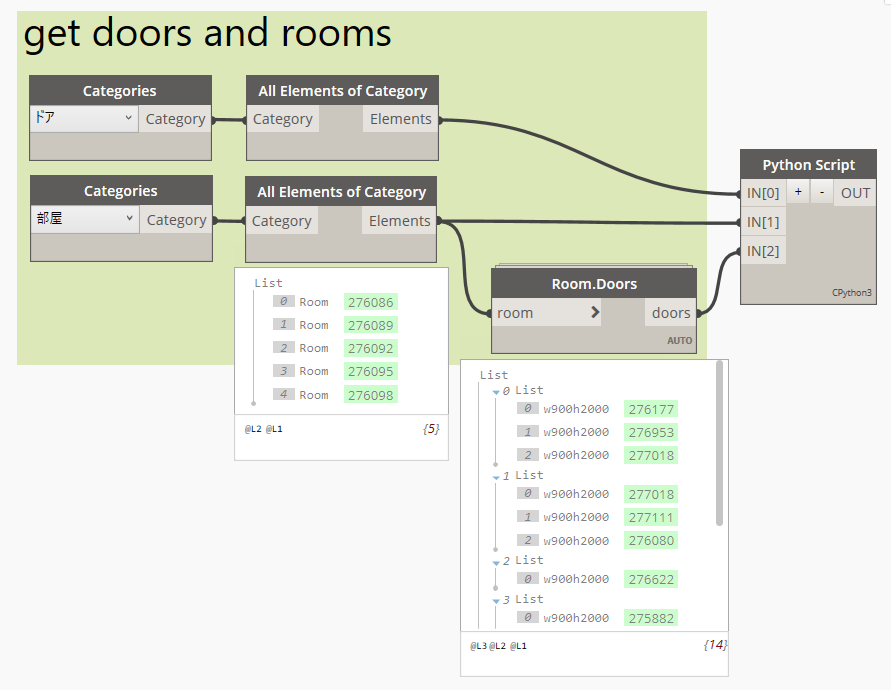
nx.Graph()で無向グラフをつくり、add_nodes() add_edge()で頂点と辺を追加します。また以下のようにタグ付けします。

• 頂点：基準点のXY座標
• 辺：距離（辺の重み）・部屋名

pythonスクリプト

import sys, clr
sys.path.append(r'C:\Users\<ユーザ名>\.conda\envs\Dynamo383\Lib\site-packages')
import networkx as nx
from itertools import combinations
import matplotlib.pyplot as plt

# dynamoノード
clr.AddReference("RevitNodes")
from Revit import Application
from Revit import Elements

def get_length(elem1, elem2):
    view = Application.Document.Current.ActiveView
    path = Elements.PathOfTravel.ByFloorPlanPoints(view, [elem1.Location], [elem2.Location], False)
    distance = int(path[0].GetParameterValueByName("長さ"))
    return distance    

def get_graph(doors, rooms, room_doors):
    graph = nx.Graph()
    # node
    for room in rooms: graph.add_node(room.Name, x=room.Location.X, y=room.Location.Y)
    for door in doors: graph.add_node(door.Id, x=door.Location.X, y=door.Location.Y)
    # edge
    for room, doors in zip(rooms, room_doors):
        # ドア間の経路を追加
        for door1, door2 in combinations(doors, 2):
            distance = get_length(door1, door2)
            graph.add_edge(door1.Id, door2.Id, weight=distance, name=room.Name)
        # 部屋からドアへの経路を追加
        for door in doors:
            distance = get_length(room, door)
            graph.add_edge(room.Name, door.Id, weight=distance, name=room.Name)
    return graph
    
graph = get_graph(IN[0], IN[1], IN[2])

グラフを描画する

matplotlib を使ってグラフを描画します。NetworkX は標準で日本語フォントに対応していないため、フォントを指定する必要があります。

pythonスクリプト

import matplotlib.pyplot as plt

def draw_graph(graph):
    pos = {i : [tag["x"], tag["y"]] for i, tag in graph.nodes(data=True)}
    edge_labels = {(i, j) : str(tag["weight"])+"\n"+tag["name"]  for i, j, tag in graph.edges(data=True)}
    nx.draw_networkx_edge_labels(graph, pos, edge_labels=edge_labels, font_family="MS Gothic")
    nx.draw_networkx(graph, pos, with_labels=False, alpha=0.5)
    plt.axis("off")
    plt.show()
    
draw_graph(graph)

実行すると以下のようなグラフが表示されます。

グラフを保存する

Dynamoのデータを保存する方法として、Revitの拡張ストレージに保存する方法と、JSONファイルやテキストファイルで出力する方法があります。今回はJSONファイルで保存します。

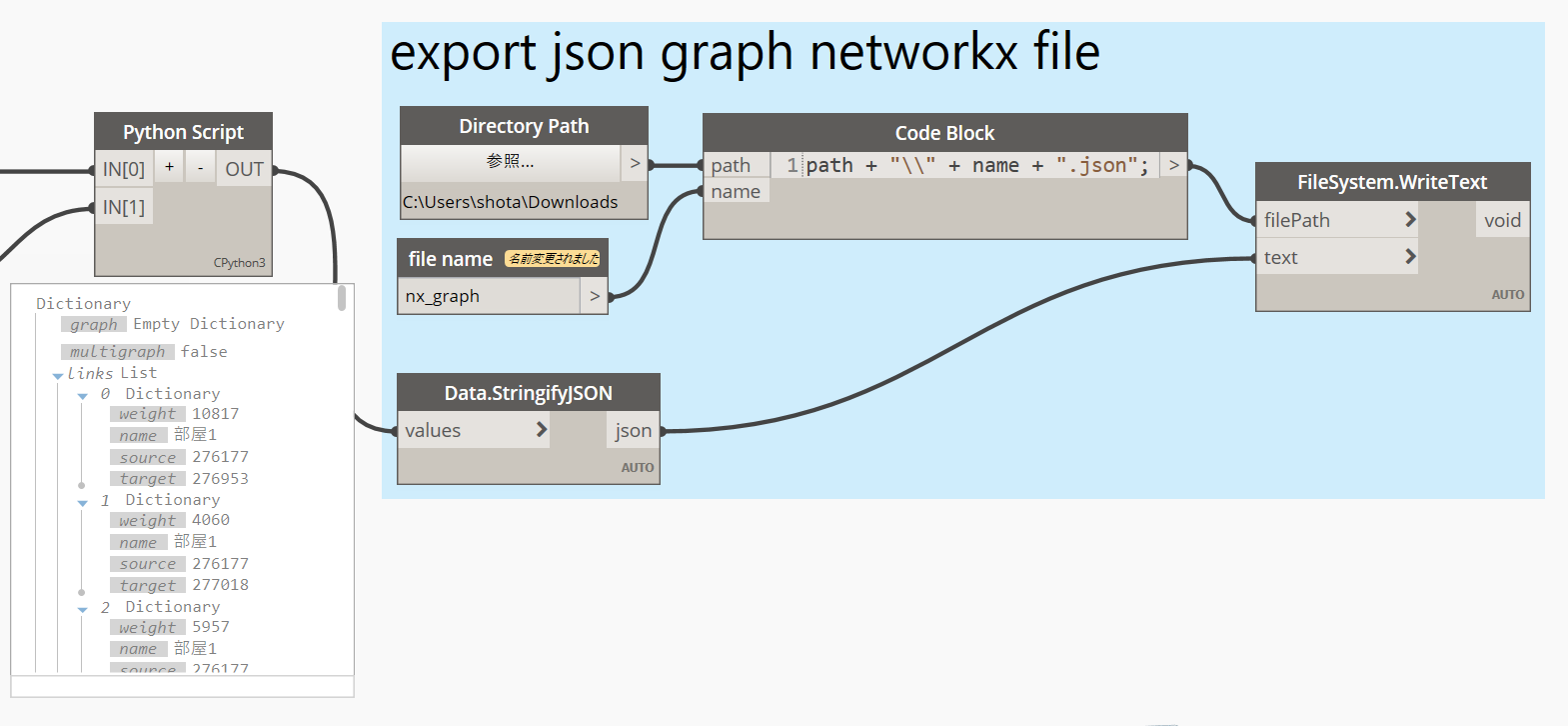
readwrite.json_graph.node_link_data()でグラフをJSONに変換します。

pythonスクリプト

OUT = nx.readwrite.json_graph.node_link_data(graph)

DynamoのFileSystem.WriteTextでJSONファイルとして保存します。

2部屋間の最短経路を求める

ここからはRevit・Dynamoは必要ないので、Google Colab等を使用しても構いません。

スタートの部屋からゴールの部屋までの最短経路を求める問題は 単一始点最短経路問題（SSSP：Single Source Shortes Path） として解決することができます。SSSPとは、$V$ 頂点と $E$ 辺からなるグラフについて、ある頂点から他のすべての頂点への最短経路を求める問題です。これを解くためのアルゴリズムとして、以下のようなものがあげられます。

• 幅優先探索（BFS：Breadth First Search）
  • 重みなしグラフで使える
  • 計算量は $O(E)$
• フォードベルマン法
  • 重み付きグラフで使うことができ、負の閉路を検出できる
  • 計算量は $O(VE)$
• ダイクストラ法
  • 負の辺を含まない重み付きグラフで使える
  • 計算量は $O(E\log V)$

今回はグラフの各辺に正の重み（距離）を与えているので、ダイクストラ法が最適です。

グラフをロードする

JSONファイルからグラフを復元します。

pythonスクリプト

import sys, json
sys.path.append(r'C:\Users\<ユーザ名>\.conda\envs\Dynamo383\Lib\site-packages')
import networkx as nx

def read_json_file(path):
    with open(path, "r", encoding="utf-8") as json_file:
        json_data = json.load(json_file)
    return nx.readwrite.json_graph.node_link_graph(json_data)
    
graph = read_json_file(<ファイルパス>)

2部屋間の最短経路を求める

経路の始点・終点として「部屋1」と「部屋4」を指定しnx.dijkstra_path()で最短経路を取得します。

pythonスクリプト

def get_shortest_path(graph, start, goal):
    path = nx.dijkstra_path(graph, start, goal)
    return path

path = get_shortest_path(graph, "部屋1", "部屋4")

グラフを描画する

matplotlib を使ってグラフを描画します。

pythonスクリプト

import matplotlib.pyplot as plt

def draw_graph_highlight(graph, path):
    path_edges = set(zip(path, path[1:]))
    pos = {i : [tag["x"], tag["y"]] for i, tag in graph.nodes(data=True)}
    edge_labels = {(i, j) : str(tag["weight"])+"\n"+tag["name"]  for i, j, tag in graph.edges(data=True) if (i, j) in path_edges or (j, i) in path_edges}
    nx.draw_networkx_edge_labels(graph, pos, edge_labels=edge_labels, font_color='blueviolet', font_family="MS Gothic")
    nx.draw_networkx(graph, pos, with_labels=False, alpha=0.5, edge_color='steelblue', node_color='steelblue')
    nx.draw_networkx_edges(graph, pos, edgelist=path_edges, alpha=0.5, edge_color='deeppink')
    nx.draw_networkx_nodes(graph, pos, nodelist=path, alpha=0.5, node_color='deeppink')
    plt.axis("off")
    plt.show()

draw_graph_highlight(graph, path)

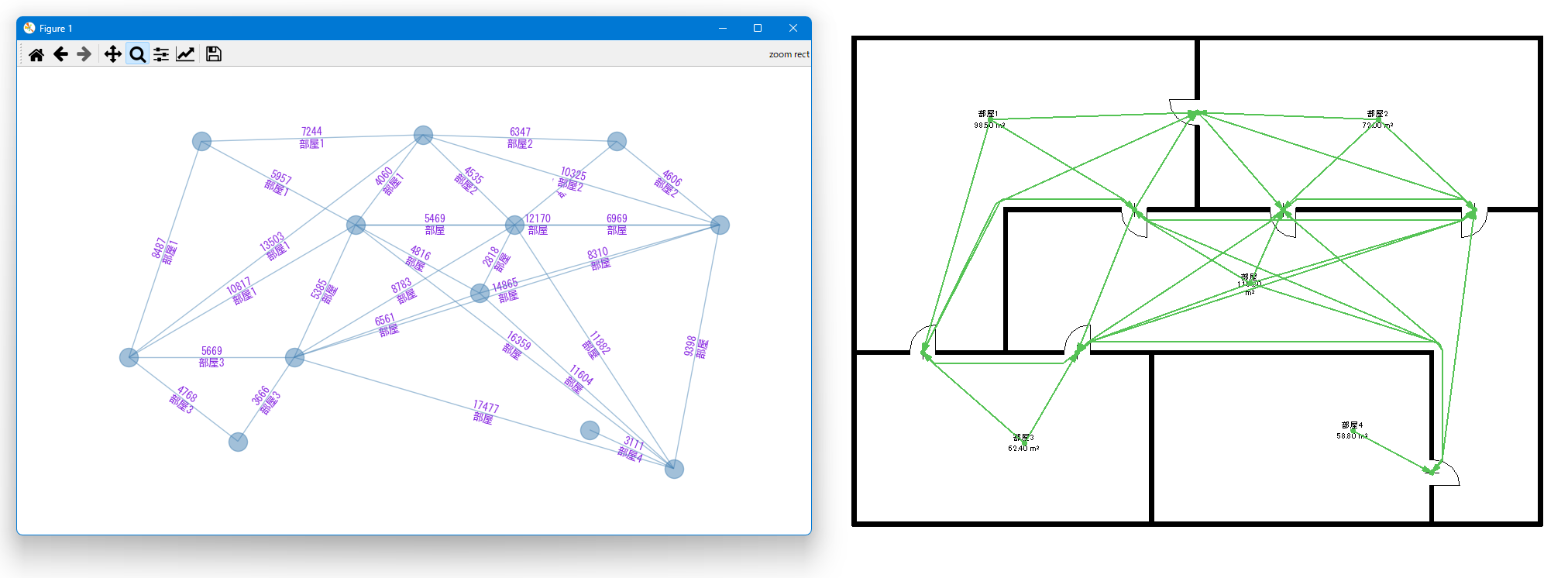
実行すると以下のようなグラフが表示されます。

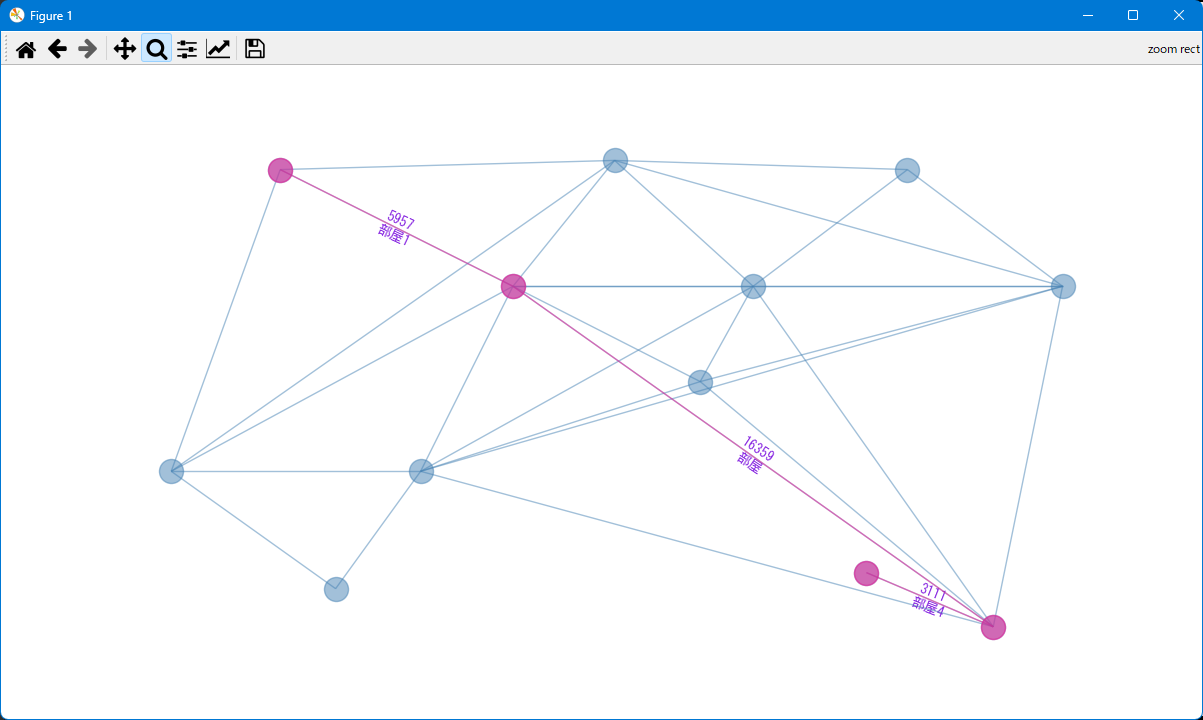
グラフから「部屋1」→「部屋」→「部屋4」が最短経路で、距離は約25mであることが分かります。

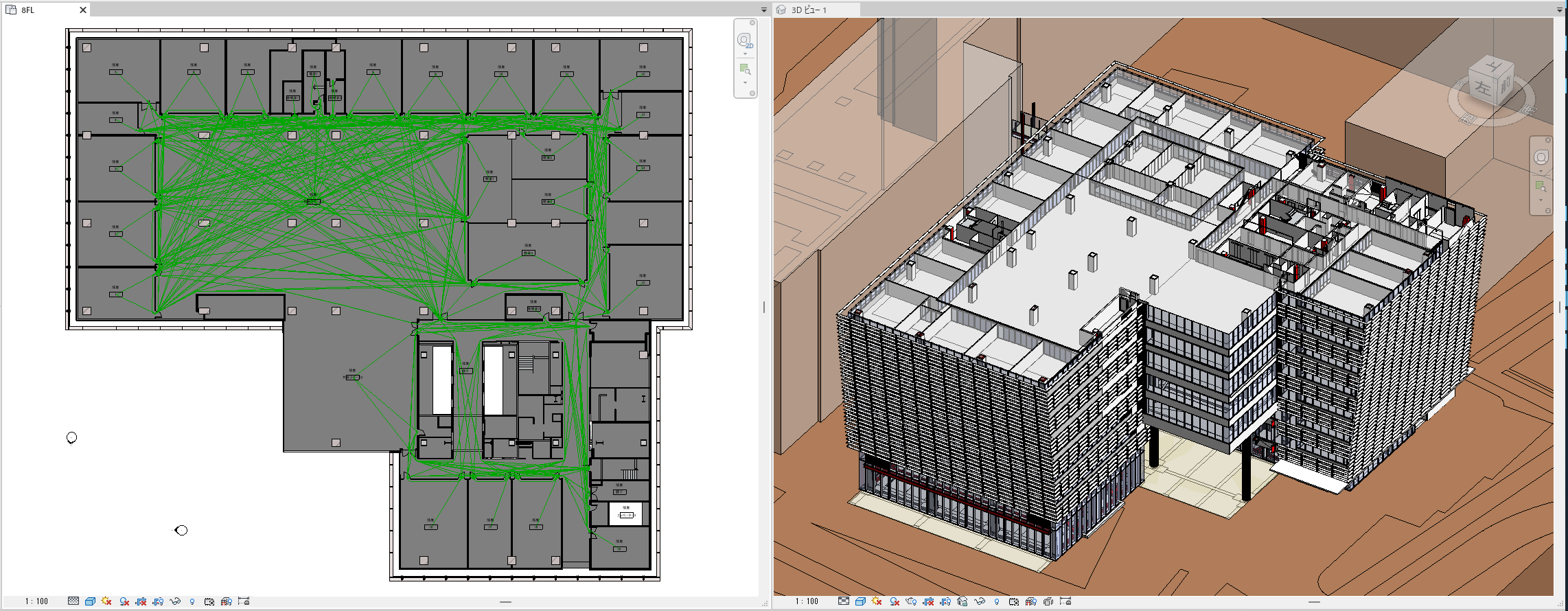
実際の建物で試す

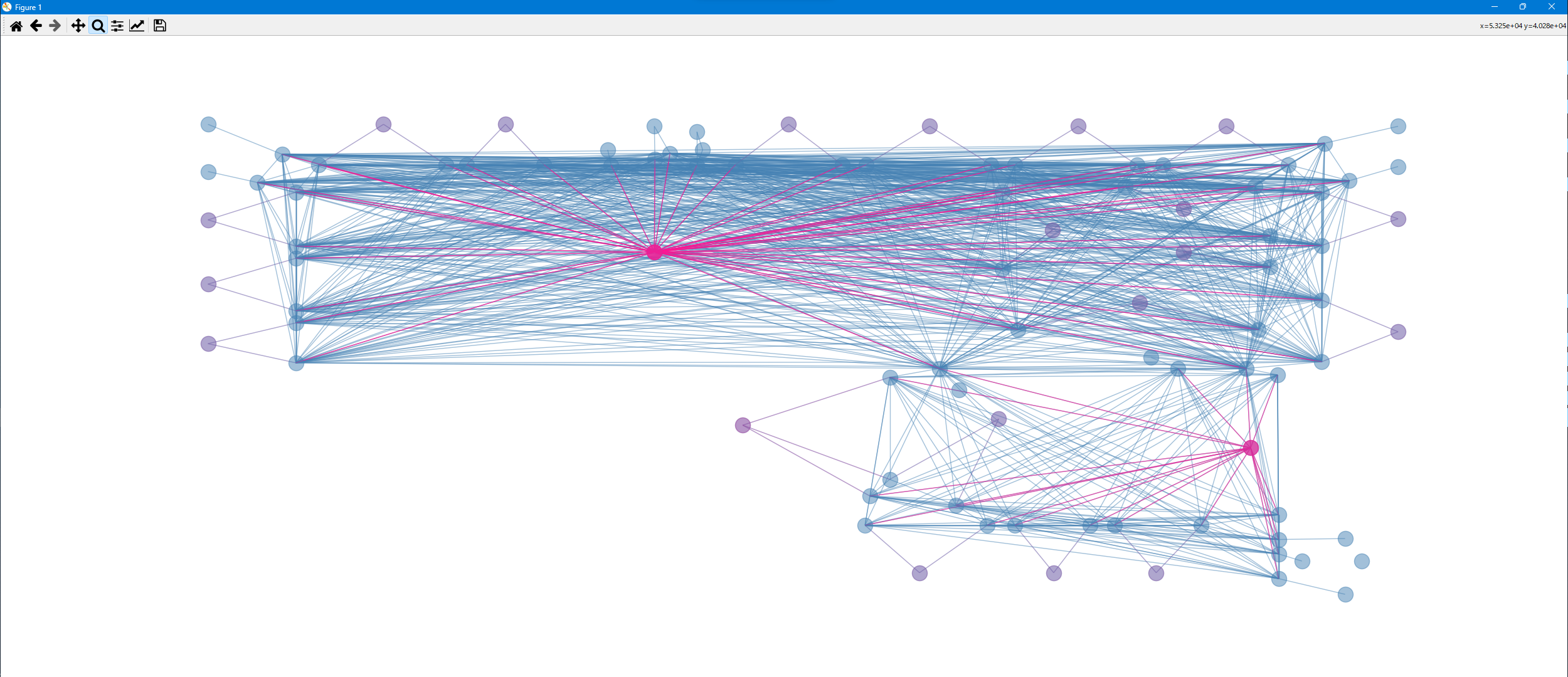
3700平米、32部屋のフロアでグラフマップをつくります。 PathOfTravel は比較的重い処理であるため、全てのパスを算出するのに20秒ほどかかります。

作成したグラフをつかってフロア中央にある「共有スペース1」から南端になる「部屋19」までの経路を算出します。

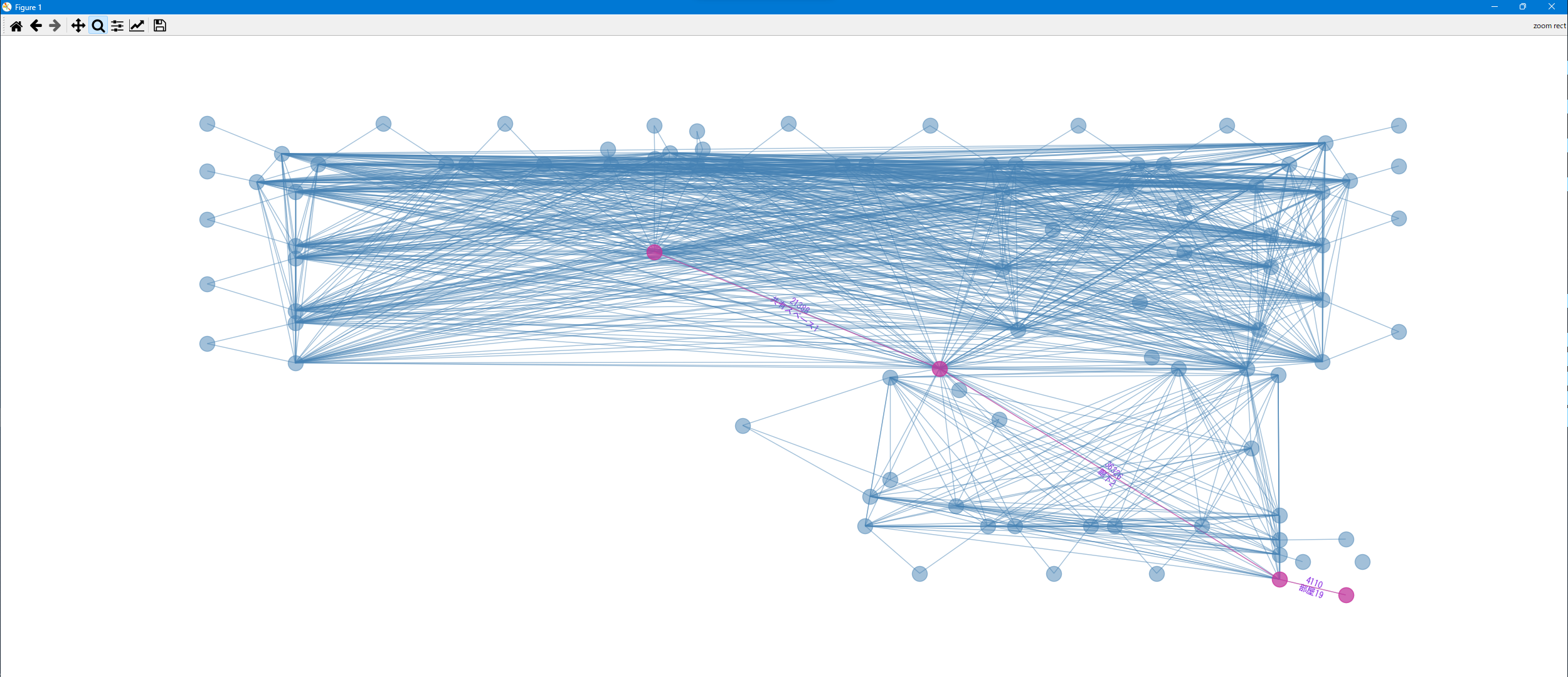
グラフから「共有スペース1」→「廊下2」→「部屋19」が最短経路で、距離は約62mであることが分かります。

おまけ

NetworkXにはnx.dijkstra_path()以外にも様々な関数が用意されています。

エレベーターホールから最も遠い部屋を調べる

nx.single_source_dijkstra_path() nx.single_source_dijkstra_path_length()でエレベーターホールから各部屋までの最短経路と距離を取得し、最も遠い部屋を求めます。

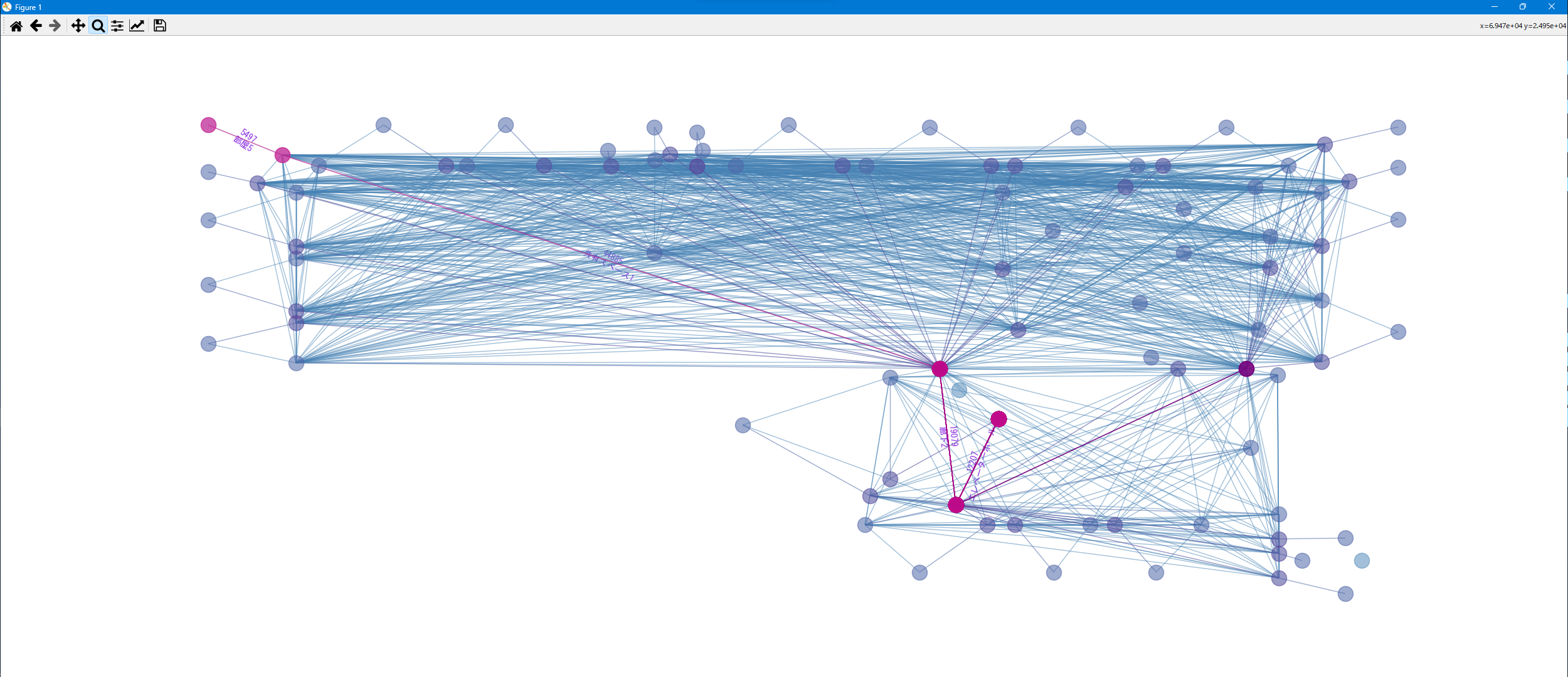
各部屋に接続する部屋数を調べる

nx.edges()でそれぞれの部屋に接続する部屋数を取得し、より多くの部屋と接続する部屋を求めます。

参考リンク