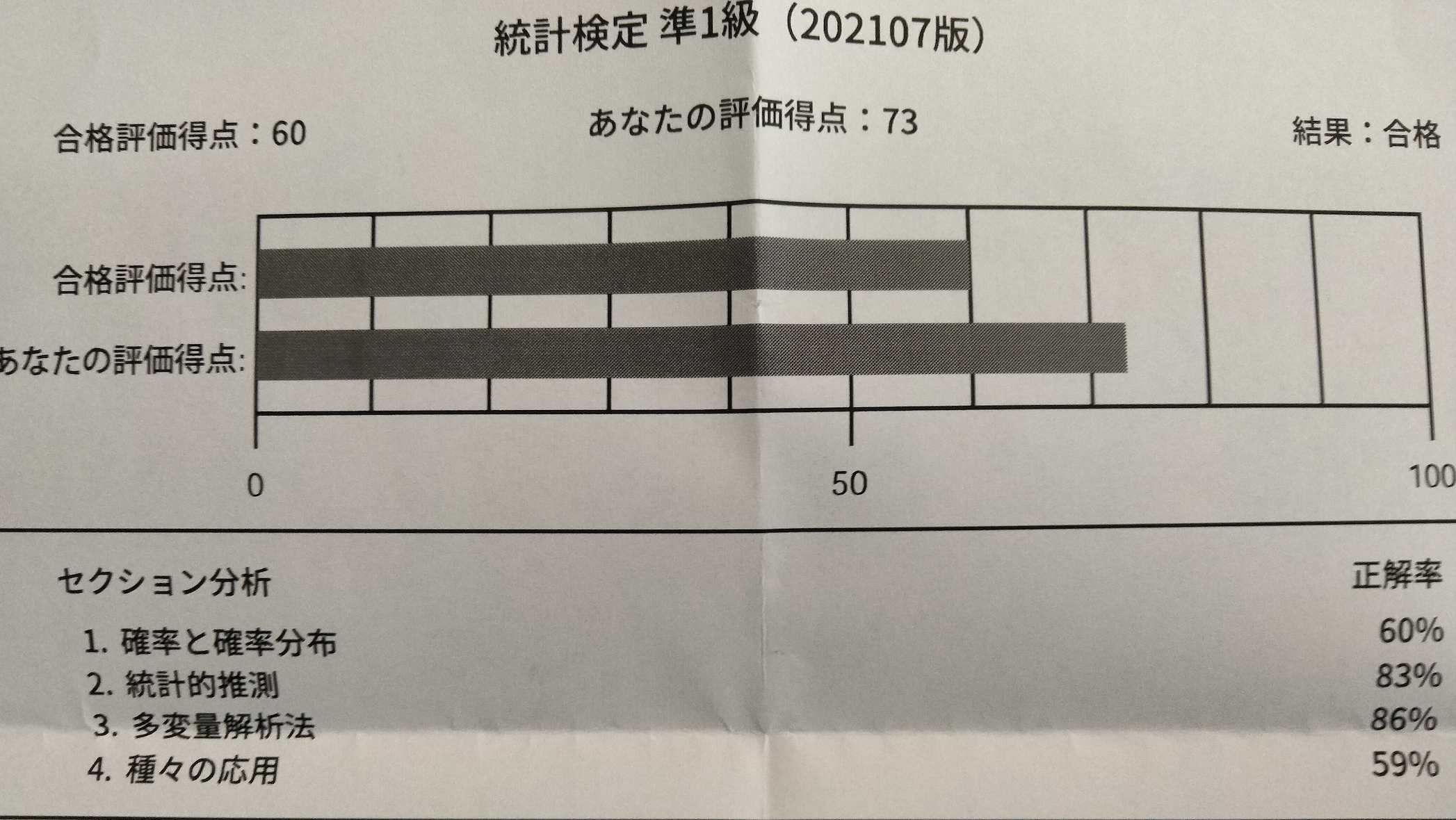
先日統計検定準１級に合格することができました。
誰かの何かの役に立つと思うので記事に残そうと思います
※合格メソッドとかではないので責任は持てません！

確率と種々の応用は計算ミスした記憶があり無念です。
算数が苦手なのがこういうところに響きましたがなんとか合格できました。

私の紹介

37歳
経済学部出身（統計はそれなりにやってたけど嫌いだった、数学は結構得意）
お仕事的には経営企画とか人事とかやってきた
なんとなく面白そうなのでデータアナリストになった。３年目
３年前に統計検定2級合格
ツイッターはこちら※特に有益なことはいわないです

こんな人です。情報とか統計を専攻していた訳ではないので準１級は結構ハードルが高かったです。勉強した内容と資格合格に向けた戦略を以下の手順で書いていきます。1回受けてダメだったので戦術を見直したことも記載していきます。

この記事で書いてること/書いてないこと/ターゲット
資格の全体像
基本戦略
戦術的失敗とその見直し
必要な数学の知識
参考文献
各章の勉強
まとめ

1.この記事で書いてること/書いてないこと/ターゲット

資格勉強とは合格するためにするものだという前提を取ります。よってここにはなんとか合格ラインまで行く方法を書いています。統計学や数学の深い本質理解的なことは記載しません。それって統計学の勉強になってるの？って批判はありそうですが目的はそれぞれということでご容赦ください。
ですのでターゲットは大学で数学とか統計学を学んでいない時間があまりないけど合格したい大人とします。

2.資格の全体像

結果レポートを見てわかる通り統計検定準１級（以下準１級）は大きく４分野から出題されます。

確率と確率分布
統計的推測
多変量解析
種々の応用

合格ラインは60点です。
私の場合、色々勉強しながらやっているので取り組んだ勉強時間は正確にはわかりませんが概算で200時間程度です。

3.基本戦略

100点満点で60点。私はこういう場合には基本戦略として8割の範囲を8割とるを採用します。理論上はこれで64点獲得できるので合格です。統計検定2級の時も同じ戦略で合格しています。これまでの資格試験も大体これでOKでした。これに則り統計学実践ワークブック全32章の8割である26章を勉強のターゲットにしました。難しそうな6章分は捨てて26章分をほぼ完璧（=8割）にします。これでボチボチ勉強しました。この勉強で過去問は全ての年で8割程度まで解くことができるようになりました。これならいけるだろうとCBT試験に挑みます。

1回目の得点は58点で不合格でした。正直なところ試験中に「あ、これ無理だ」ってなってたので58点も取れたことは意外でした。しっかり勉強したはずなのですが過去問（2021年除く）より遥かに難易度が高い印象でした。58点なのでもうちょっと勉強したら合格するやろってなるのが普通だと思いますが、次で合格する気がしなかったので戦術を見直すことにしました。

4.戦術的失敗とその見直し

1回試験を受けて感じたことは以下です。

難易度は2021 > 各年の論述問題 > CBT >> 2019年以前
暗記では解けないように工夫されている
難問がいくつか用意されている
ワークブックに1行だけ記載されているようなことが主題される
計算問題が多く時間ギリギリ

でした。戦術を修正する必要があります。なぜかというと8割8割戦略は8割の範囲をしっかり把握することが前提です。

最も重要な戦術的ミス

ここで私は重大なミスをしていました。それは難しそうな６章分を捨てるということです。なんとなく難しそうだという理由で除外したため8割の範囲を勉強できていなかったんだということがわかりました。
具体的に１回目に捨てた章は以下です。

第４章変数変換
第７章極限定理、漸近理論
第１３章ノンパラメトリック法
第１５章確率過程の基礎
第２７章時系列解析
第３２章シミュレーション

ワークブックを読んでなんとなく難しいなっていう理由だけで除外しました。これが不味かった。準１級のCBT試験は全範囲満遍なく出題されており、なおかつ1行だけ記載されているようなことも問われるのですが、実はこれ自体は難問ではないんです。ワークブックに記載されている通りに回答すれば得点できるのでむしろ得点源にもなるようなものです。なんとなく難しいというだけで６章分もこういったものを切り捨ててしまったので出題に対する8割の範囲を勉強することが達成できていないことが敗因だと理解できました。よってわからなくとも細かく読み込む必要があるなと理解できました。

例えばこんな問題が出たとします。

以下の確率分布で再生性を持たないものはどれか？
 正規分布
 指数分布
 カイ二乗分布
 非心カイ二乗分布

こういうタイプ問題はその場で計算してしまう方が早いかもしれません。ワークブックに直接的にこれが記載されている訳ではありませんがちゃんと読んでいれば確実に答えられる問題です。こういったものを落とすのは非常に勿体無いです。

そこで8割の範囲を勉強したぞ！という定義を変更しました。章で考えるのではなく、４分野それぞれ８割と捉え直しました。章ではなくそれぞれの分野の理解度（=試験で出れば解ける問題）を８割にしようということです。こう書くと初めからそうしろよって感じがします。

ipadでの勉強の弊害

私は普段からipadをノートにして勉強しており、ノートアプリの投げ輪機能を多用しています。これは自分で書いた文字を範囲コピーしたりそのまま移動させたりできるものです。これは同じような数式を何回も書くことになる時にはめちゃくちゃ便利なのですが使いまくっていたせいで本番では計算が思った以上に時間がかかってしまいました。本番と同じ状態で勉強するというのはやはり大事ですね。しばらく投げ輪機能を封印することにしました

試験を受け戦術を見直した収穫

漠然と32章もあるテキストを読むのではなく大きく４分野があることを意識することができるようになりました。32章を４つに分けることでどの章とどの章が絡んでいるのかを俯瞰できるようになり学習効率がめちゃくちゃ上がりました。なのでこれから受ける人はこれ絶対にやった方がいいです。４分野で得意苦手が分かれば重点的に勉強しなければならないポイントが見えてきます。資格もマーケも傾向と対策です。

計算時間の短縮

ラスト１週間は計算する演習に集中しました。これで計算速度がかなり早くなりました。１回目はちょっと時間足りないくらいでしたが、２回目は20分程度残り、余裕を持って見直しができました。この余裕は大きいです。見直しの中でいくつかミスを発見できました。自由度の設定ミスやマークミスがありました。危ない危ない

5.必要な数学の知識

高校までの数学はもちろんですが、線形代数や微積分の知識がないとそもそもワークブックの内容を理解できないシーンが出てきます。大学でちゃんと数学をやっていない人はそのあたりをしっかりおさえる必要があります....

というよくある感想では意味がないのでもっと具体的な話をしたいと思います。
けっこう大胆なことを言っている気がしますが合格が目的ですのでご容赦ください。

線形代数

私は大学で線形代数をあまりちゃんとやっていないのでしっかり勉強しようと思い学習したのですが正直そこまで勉強する必要ないです。どこまでやればいいかわからなかったので気がついたらフーリエ変換あたりまで勉強してました。おかげでワークブックの内容程度であれば難なく読み解けるようにはなりましたが資格合格を考えるとオーバースペックです。ワークブックに記載されている計算を自分で書ける程度の理解が最低限必要な知識でしょうか。

ベクトルと行列の積
行列と行列の積
行列式の求め方
逆行列の求め方
固有値、固有ベクトルの求め方
対角化

あたりが最低限かなーと思います。線形代数を理解することよりもワークブックに書いている計算を自分でできるようになることに集中した方がいいです。線形代数は奥が深すぎて沼です。そして楽しいです、戻ってこれなくなります。あとは「へー、実対称行列の固有値は実数なんだー」「へー、標本相関行列みたいな$A=B^\top B$っていう場合にはAの固有値は非負なんだー」などワークブックに書いていることをそのまま受け入れておくと良いです。

微分積分

大学の微分積分の教科書を持ってくるよりも確率密度関数を微分したり積分したりしましょう。できれば主要な確率分布なら全部できるように。大学の教科書を持ってくると三角関数の微分とか逆三角関数とかが出てきます。これはこれで大事なんですが準1級の試験に必要？って言われると使わないと思います。それより合成関数の微分や関数の積の積分、部分積分や置換積分など高校でも習う内容を使いこなす方が優先です。関数が連続かどうか調べる機会は少なくとも準1級を合格するまでにはしないと思います。モーメント母関数から期待値や分散を求めまくりましょう。良いトレーニングになりますし試験でも使うタイプの計算です。

6.参考文献

ワークブックは必須ですがこれは教科書ではありません。試験範囲が書かれているものだと割り切りましょう。ワークブックだけ見て「うんうん、なるほどねー」と理解できる人は明日には合格できます。私が使った勉強のお供をご紹介します。（ワークブックと過去問は必須なので除外）

統計学入門
赤本です。大体これでどうにかしてます。確率の基礎から回帰分析あたりまではこれ１冊でどうにかなると思います。

ガイダンス確率統計
資格勉強には使っていないのですが最近これで勉強し直しています。赤本の行間を埋めるために調べたり勉強したことがしっかり載ってます。赤本が辛いって人はここから始めてもいいのではないかなーと思いご紹介。

多変量解析法入門
多変量解析についてはこれがとても良かったです。どういう状況でその手法を使うのか、その結果をどう解釈するのかがガイドされているのでこれを一通り勉強してからワークブックを見ると「よくこのページ数でまとめたな」とワークブックに感心してしまいます。

ベイズ統計の理論と方法
難しかったですがすごく力がついた感じがします。30~32章の範囲のことが色々書いているのですがその範囲はこの本でしか勉強してないです。でももうちょっと平易な本があると良かったなーという印象。

7.各章の勉強

合格に向けた各章の私的なポイントをざっと紹介。
章末問題は解けるようになりましょう。これは全章共通です。

第１章

包除原理やベイズの定理はしっかりおさえましょう。ベイスの定理は統計検定２級では

P(A|B) = \frac{P(B|A)P(A)}{P(B)} = \frac{P(A\cap B)}{P(B)}

の形で覚えている人も多いかと思いますがこれを

P(A|B) = \frac{P(B|A)P(A)}{P(B|A)P(A)+P(B|A^{c})P(A^{c})}

丁寧に場合わけする手続きにとは慣れておくと良いです。この発想が問題を解くポイントになることがしばしばあります。
章末例題はぬるいのでこれくらいはすぐに解けるようにしましょう。

第３章

歪度・尖度も問題にしやすいと思うので理解しておきましょう。t分布と正規分布の歪度・尖度比較とかありそう。

第4章

ヤコビアンは慣れてないとギョッとしますがやってることは難しくないです

第5章

各分布の特徴と確率関数はなんとなくでも覚えておきましょう

第6章

各分布の特徴と確率関数はなんとなくでも覚えておきましょう

第7章

深い理論背景を追うのではなくそういうもんなんだなと理解しましょう
ここがわからないからといって１から確率の勉強をするのは資格合格に対して効率よくないです

第8章

7章と同じく。章末問題を解けるようになれば自然と何を言ってるかわかってきます

第9~12章

統計検定2級範囲+αくらいです。そのせいか準1級の勉強をしていると疎かになりがちです。どんな時にどの分布使うのか、自由度はなんだっけみたいなことは寝起きでもできるようになっておきましょう

第13章

発想はすごくシンプルなので丁寧に読めば理解できます。
クラスカルウォリス検定の検定統計量とかはギョッとしますが「$(x-\bar{x})^2$みたいだなぁ」というようなことに気付いていくと覚える量がどんどん減ります。

第14章

図を描きながら理解すれば難しくないです。
文章を式にする部分を間違えないように。

第15章

これまでのいくつかの章の組み合わせっぽいので慎重に読めば理解できます。

第16章

めっちゃ大事です。
重回帰は行列の形と記号（$SyyとかSxyとか$）どっちでも解けるように。
L1とL2とElastic-netの見分けができるように。

第17章

読んだらわかる。わからない場合は重回帰の仮定とかその辺の知識不足。
４つの図から元の散布図と回帰直線をイメージできるくらいになれば強い

第18章

どういう値を推定しているのかを間違わないようにすれば平気。
logとexpの関係とか基礎的な部分を再度おさえる

第20章

直交表ちゃんと勉強しよう

第21章

ネイマン配分法を覚える

第22~26章

式の導出、結果の解釈をできるように。
小さいデータセットで手計算させることが多そうなのでできるようになっておく。

第27章

ARとMAの見分け大事。コレログラムからの読み解きは必須。
DWは計算方法を知っているかいないかなので絶対おさえる

第28章

よく考えれば物凄く当たり前で納得感のあることを数学で説明しているので難しく感じる。
要するにこういうことだよねってポイントを押さえていく
階層モデルは楽しい

第29章

処理方法によってどんな偏りが発生するのか。それはなぜか。
小さいデータセットで自分で色々試して見るのが早い。難しいことは言ってないので知識の整理

第30章

モデル選択の計算方法、特徴の比較をおさえる。AIC、BIC、CV。

第31章

事前分布、得られたデータ、事後分布をベイズの定理の式に当てはめれば何が起きているか理解できる。
パーツに分けてそれぞれの役割を丁寧に理解する

第32章

手法の発想そのものは素直なのでそれをまず理解。その後に理屈と計算方法を整理する

まとめ

勉強すればするほどわからないことが増えていく感覚になるので「どこまで理解すればいいんだろう」という疑問が常に付き纏うのではないかなと思います。CBTはいつでも受けられるのでお金に余裕があればワークブック一周したくらいでとりあえずどのくらい理解しなきゃいけないかを知ることを目的に受けちゃうのもありだと思います。私は偶然にもそうなりました。加えて過去問はありますがそもそも試験範囲が広すぎて練習問題が足りない問題に陥りやすいので試験受けにいくは有効なはずです。

合格したけど統計まじでなんもわからん状態になったので勉強しなきゃって思わせてくれる良い試験でした。
この記事が何かの役に立つと嬉しいです。

１級は来年くらいに取り組もうかな。

追記：2023/9/10
優秀成績賞だったようで統計検定公式サイトに名前載ってました！

統計検定準１級に合格するまでの道のり【追記あり】