はじめに
今回は緯度経度から2地点間の距離を求めます.GoogleのAPIやMathematicaなど様々な場所で2点間の距離を求める計算が行えますが,これらの計算を行うにあたって地球は回転楕円体なので正確に2地点間の距離を求めることが難しいです.そこで,この課題を解決する主な手法をいくつか取り上げて比較したいと思います(公式の導出等の詳細な理論については割愛します).
主な手法として以下のものがあります.
- Haversineの公式
- Hubenyの公式
- Vincenty法
- 測地線航海算法(Geodesic Sailing)
- 国土地理院の方法
- GeographicLibライブラリを用いる
また,地球を回転楕円体として扱う上では以下のようなモデルがあります.現在では,GRS80とWGS84は事実上同一のものとなっています.
| 長半径[m] | 短半径[m] | 扁平率 | 平均半径 | 備考 | |
|---|---|---|---|---|---|
| GRS80 | 6,378,137 | 6,356,752 | $$\frac{1}{298.257222101}$$ | 6,371,008.771 | 世界標準の測地系 |
| WGS84 | 6,378,137 | 6,356,752 | $$\frac{1}{298.257223563}$$ | 6,371,008.771 | GPSの測地系などに使用されている |
| Bessel | 6,377,397.155 | 6,356,078.963 | $$\frac{1}{299.152813}$$ | 6,370,291.091 | 旧日本測地系 |
今回は回転楕円体としてGRS80を扱います.
Vincenty法と国土地理院の方法については実装は行わず,概要だけ取り扱います.その他の手法については実装を行い,その比較を行おうと思います.実装はC言語で行いますが,標準ライブラリしか扱わないのでぜひ他の言語にも応用してみてください!!
Haversineの公式
世界的に様々な場面で使用されている計算手法で,球面三角法を用いて地球を理想的な球体として扱います.詳しい説明は色々なところで説明されていますので省きますが,下図を用いてざっくり説明すると,球面上に北極点と扱う2点A,Bで球面三角形をつくり,球面三角法の余弦定理を用いて2地点間の距離Dを求めています.

公式にすると次のようになります.
地点A : (経度x1, 緯度y1) 地点B : (経度x2, 緯度y2)\\
2地点間の距離 : D = R\cos^{-1}(\sin y1\sin y2 + \cos y1\cos y2\cos\Delta x) \\
\Delta x : x2 - x1\\
赤道半径 : R = 6378.137[km]
これをそのまま実装してみます.
#include <stdio.h>
#include <math.h>
double EARTH_RAD = 6378.137; // km
double deg2rad(double deg) {
return deg * M_PI / 180.0;
}
double cal_distance(double x1, double y1, double x2, double y2) {
/*
pointA(lng x1, lat y1), pointB(lng x2, lat y2)
D = Rcos^-1(siny1siny2 + cosy1cosy2cosΔx)
Δx = x2 - x1
R = 6378.137[km]
*/
return EARTH_RAD * acos(sin(y1) * sin(y2) + cos(y1) * cos(y2) * cos(x2 - x1));
}
int main(void) {
// ここではAを東京駅,Bを東京スカイツリーとしています.
double A[2] = {139.76709260881086, 35.6812710316305}; // pointA (lng, lat)
double B[2] = {139.81066223501705, 35.70996120396507}; // pointB (lng, lat)
// degrees to radians
A[0] = deg2rad(A[0]);
A[1] = deg2rad(A[1]);
B[0] = deg2rad(B[0]);
B[1] = deg2rad(B[1]);
double distance = cal_distance(A[0], A[1], B[0], B[1]);
printf("distance: %.8f\n", distance);
return 0;
}
この手法が今回紹介するものの中で一番簡潔に実装できます.後に精度の比較を行いますが,地球を球とみなすのでモデル誤差が生じてしまいます.
Hubenyの公式
主に日本の計算サイトなどで用いられている公式で,これもざっくり下図を用いて説明すると,まず,2地点A,Bの中点Rにおける回転楕円体の子午線方向と卯酉線方向のそれぞれの曲がり具合を円で近似します.次に2地点A,Bの経度差をΔx,緯度差をΔyとし,回転楕円体の近似円の子午線方向の曲率半径をM,卯酉線方向の曲率半径をNとします.点Aと経度が等しく,点Bと緯度が等しい点Hをつくって直角三角形をつくります.角AOH=Δyと書けるのでAH≒MΔyと近似でき,Rの緯度をμとすると線分BHもBH≒NcosμΔxと近似できます.この線分AHと線分BHを利用して求める距離である線分ABを3平方の定理で導きます.

今回扱っているHubenyの公式はカシミール3Dなどで用いられている簡易版でオリジナルのものではないので注意してください.
公式は次のようになります.
地点A : (経度x1, 緯度y1) 地点B : (経度x2, 緯度y2)\\
2地点間の距離 : D = \sqrt{(M\Delta y)^2+(N\Delta x\cos \mu)^2}\\
\Delta x : x2 - x1\\
\Delta y : y2 - y1\\
\mu : \frac{y1 + y2}{2}\\
子午線曲率半径 : M = \frac{Rx(1-E^2)}{W^3}\\
卯酉線曲線半径 : N = \frac{Rx}{W}\\
W = \sqrt{1-E^2\sin^2\mu}\\
離心率 : E = \sqrt{1-(\frac{Ry}{Rx})^2}\\
Rx : 回転楕円体の長半径(赤道半径) Ry : 回転楕円体の短半径(極半径)
これを実装すると以下のようになります.
#include <stdio.h>
#include <math.h>
double RX = 6378.137; // 回転楕円体の長半径(赤道半径)[km]
double RY = 6356.752; // 回転楕円体の短半径(極半径) [km]
double deg2rad(double deg) {
return deg * M_PI / 180.0;
}
double cal_distance(double x1, double y1, double x2, double y2) {
double dx = x2 - x1, dy = y2 - y1;
double mu = (y1 + y2) / 2.0; // μ
double E = sqrt(1 - pow(RY / RX, 2.0)); // 離心率
double W = sqrt(1 - pow(E * sin(mu), 2.0));
double M = RX * (1 - pow(E, 2.0)) / pow(W, 3.0); // 子午線曲率半径
double N = RX / W; // 卯酉線曲率半径
return sqrt(pow(M * dy, 2.0) + pow(N * dx * cos(mu), 2.0)); // 距離[km]
}
int main(void) {
// ここではAを東京駅,Bを東京スカイツリーとしています.
double A[2] = {139.76709260881086, 35.6812710316305}; // pointA (lng, lat)
double B[2] = {139.81066223501705, 35.70996120396507}; // pointB (lng, lat)
// degrees to radians
A[0] = deg2rad(A[0]);
A[1] = deg2rad(A[1]);
B[0] = deg2rad(B[0]);
B[1] = deg2rad(B[1]);
double distance = cal_distance(A[0], A[1], B[0], B[1]);
printf("distance: %.8f\n", distance);
return 0;
}
この手法では直角三角形をうまく平面に射影できたときに精度が出ます.そのため,高緯度の地点を含む距離を計測するときには正確でない場合が多く,測地線の長さよりも緯線に沿った長さのほうが長いので,多くの場合,正確な長さよりも計算結果が大きくなります.直角三角形が子午線方向に長いときには精度が高く,測地線がその近辺の緯線と大きく異なるとき誤差が大きくなります.
Vincenty法
Vincenty法は回転楕円体モデルを使用して測地線距離を計算する公式の1つで,誤差0.5mm以内という精度の良さを発揮します.しかし,19,936kmを超える距離や,片方の地点に対してもう片方の地点が対蹠点から約75km以内にある場合は精度が悪くなるようです.
詳細は以下のサイトを確認してみてください.
測地線航海算法(Geodesic Sailing)
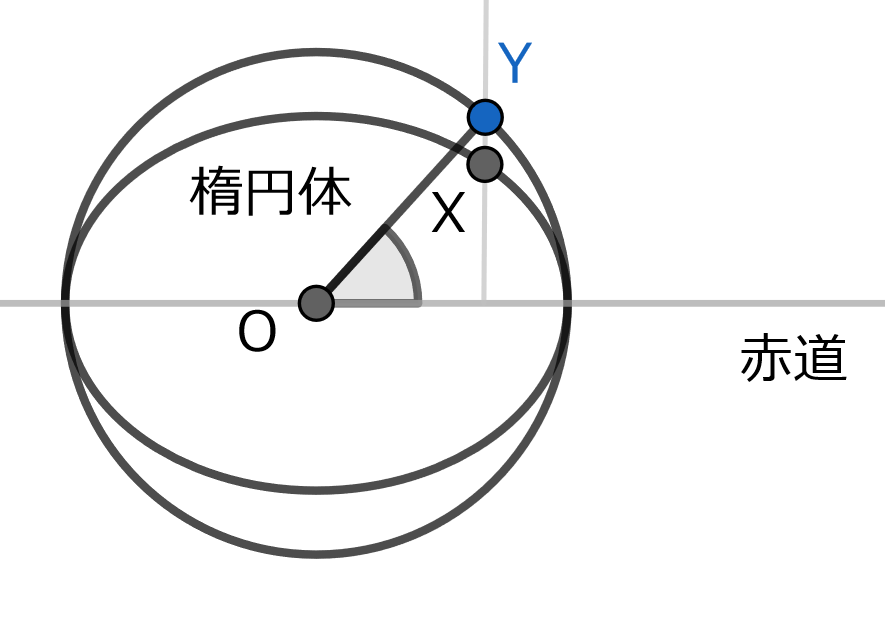
Lambertが考えた公式にAndoyerが補正を掛けたもので,測地緯度を化成緯度に変換して球面上の距離を計算し,距離補正量を算出して測地線の長さを求めます.ここで化成緯度とは下図のように,楕円体上のある地点Xにおける赤道面の法線と,楕円体と赤道で接する球面との交点Yを設定し,その交点と楕円体の中心Oを通る直線が赤道面となす角のことをいいます.
公式は以下のようになります.
地点A : (経度x1, 緯度y1) 地点B : (経度x2, 緯度y2)\\
化成緯度 : \phi = \tan^{-1}(\frac{Ry}{Rx}\tan y)\\
Rx : 回転楕円体の長半径(赤道半径) Ry : 回転楕円体の短半径(極半径)\\
球面上の距離 : X = \cos^{-1}(\sin\phi_A\sin\phi_B + \cos\phi_A\cos\phi_B\cos(x1-x2))\\
\phi_A : A点の化成緯度 \phi_B : B点の化成緯度\\
距離補正量 : \Delta\rho = \frac{F}{8}(\frac{(\sin X-X)(\sin\phi_A+sin\phi_B)^2}{\cos^2\frac{X}{2}} - \frac{(\sin X+X)(\sin\phi_A-sin\phi_B)^2}{\sin^2\frac{X}{2}})\\
扁平率 : F = \frac{Rx-Ry}{Rx}\\
測地線長 : \rho = Rx(X+\Delta\rho)
これをC言語で実装します.
#include <stdio.h>
#include <math.h>
double RX = 6378.137; // 回転楕円体の長半径(赤道半径)[km]
double RY = 6356.752; // 回転楕円体の短半径(極半径) [km]
double deg2rad(double deg) {
return deg * M_PI / 180.0;
}
double cal_distance(double x1, double y1, double x2, double y2) {
double p1 = atan(RY / RX * tan(y1)); // 地点Aの化成緯度
double p2 = atan(RY / RX * tan(y2)); // 地点Bの化成緯度
double X = acos(sin(p1) * sin(p2) + cos(p1) * cos(p2) * cos(x1 - x2)); // 球面上の距離
double F = (RX - RY) / RX; // 扁平率
// 距離補正量
double dr = F/8 * ((sin(X)-X)*pow((sin(p1)+sin(p2)), 2.0)/pow(cos(X/2), 2.0) - (sin(X)+X)*pow((sin(p1)-sin(p2)), 2.0)/pow(sin(X/2), 2.0));
return RX * (X + dr); // 距離[km]
}
int main(void) {
// ここではAを東京駅,Bを東京スカイツリーとしています.
double A[2] = {139.76709260881086, 35.6812710316305}; // pointA (lng, lat)
double B[2] = {139.81066223501705, 35.70996120396507}; // pointB (lng, lat)
// degrees to radians
A[0] = deg2rad(A[0]);
A[1] = deg2rad(A[1]);
B[0] = deg2rad(B[0]);
B[1] = deg2rad(B[1]);
double distance = cal_distance(A[0], A[1], B[0], B[1]);
printf("distance: %.8f\n", distance);
return 0;
}
このLambert-Andoyerの式を若干変形して簡単に実装できるようにした小野の公式や,この手法にさらにThomasが補正を加え,精度が良くなったものもあります.
国土地理院の方法
国土地理院で用いられている手法で,計算式は以下のサイトに載っています.
元となる論文があるようですが,概要理解が難しそうなので今回は深入りしません.安定して良い精度が得られるようなので下記の計算サイトを用いて後に比較したいと思います.
GeographicLibライブラリを用いる
測地線距離を求めるにあたって非常に精度が高いことで有名なライブラリでどのような距離でも安定して誤差15nm以内の精度で計算されるようです.アルゴリズムはこちらに記載されています.MITライセンスで,C++,C,Fortran,Python,Octave,Java,JavaScriptをサポートしています.
C言語で実装しますのでこちらのページからファイルをダウンロードします.今回は,Ver.2.1のものを使用します.Windowsの場合はコマンドプロンプトでtar -xzf (ファイル名).tar.gzとするか,7-Zipなどのソフトウェアで解凍します.geodesic.cとgeodesic.hをカレントディレクトリに置き,以下のuse_geographiclib.cとgeodesic.cを一緒にコンパイル,リンクすることで2点間の距離を求めることができます.
#include <stdio.h>
#include <math.h>
#include "geodesic.h"
double RX = 6378137; // 回転楕円体の長半径(赤道半径)[m]
double F = 1 / 298.257222101; // 扁平率
int main(void) {
// ここではAを東京駅,Bを東京スカイツリーとしています.
double A[2] = {139.76709260881086, 35.6812710316305}; // pointA (lng, lat)
double B[2] = {139.81066223501705, 35.70996120396507}; // pointB (lng, lat)
double D; // 求める距離[km]
struct geod_geodesic g; // 楕円体の情報を持つ構造体
/* Initialize geodesic */
geod_init(&g, RX, F); // 赤道半径と扁平率を指定して楕円体を初期化
geod_inverse(&g, A[1], A[0], B[1], B[0], &D, 0, 0); // 2点間の距離を計算
/* geod_inverse(楕円体の情報を持つ構造体へのポインタ, Aの緯度, Aの経度,
Bの緯度, .Bの経度, 2点間の距離のポインタ[m],
Aの方位角のポインタ(未使用), Bの方位角のポインタ(未使用)) */
printf("distance: %.8f\n", D/1000); // 距離をkmに変換して出力
return 0;
}
精度比較
各手法の概要をおさえたところで,Vincenty法を除いた5つの手法の精度の比較を行っていきます.精度の良し悪しは今回紹介した手法の中で一番正確とされるGeographicLibライブラリを用いた結果をもとに判断していきます.
まずは,非常に近い2地点間である
東京スカイツリー(35.71007721380533, 139.81070570812608) から
すみだ水族館(35.709943856092394, 139.80959161455687) で実験してみます.
| 計算手法 | 2地点間の距離[km] | 誤差[km] | 誤差比率[%] |
|---|---|---|---|
| Haversineの公式 | 0.10179058 | 0.0001067 | 0.1047 |
| Hubenyの公式 | 0.10189728 | 0 | 0 |
| 測地線航海算法 | 0.10189724 | 0.00000004 | 0 |
| 国土地理院の方法 | 0.101897 | 0.00000028 | 0 |
| GeographicLib | 0.10189728 | - | - |
100m程の距離であればどの手法を用いてもほぼ誤差なく正確に計算できることがわかります.
次に,少し離れて,
東京スカイツリー(35.71007721380533, 139.81070570812608) から
浅草寺(35.714319796934106, 139.7967684734017) で実験してみます.
| 計算手法 | 2地点間の距離[km] | 誤差[km] | 誤差比率[%] |
|---|---|---|---|
| Haversineの公式 | 1.34536380 | 0.00080416 | 0.0597369 |
| Hubenyの公式 | 1.34616797 | 0.00000001 | 0 |
| 測地線航海算法 | 1.34616741 | 0.00000055 | 0 |
| 国土地理院の方法 | 1.346168 | 0.00000004 | 0 |
| GeographicLib | 1.34616796 | - | - |
1km程でも先程と変わらず良い精度が出ています.Haversineの公式でも1m弱程の誤差に収まっています.
さて,今度は一気に大阪まで行っちゃいましょう!!
東京スカイツリー(35.71007721380533, 139.81070570812608) から
JR大阪駅(34.702423397783264, 135.495825762501) で実験してみます.
| 計算手法 | 2地点間の距離[km] | 誤差[km] | 誤差比率[%] |
|---|---|---|---|
| Haversineの公式 | 408.14263894 | 0.31686427 | 0.077575 |
| Hubenyの公式 | 408.50135460 | 0.04185139 | 0.010246 |
| 測地線航海算法 | 408.45939856 | 0.00010465 | 0 |
| 国土地理院の方法 | 408.459503 | 0.00000021 | 0 |
| GeographicLib | 408.45950321 | - | - |
400km程離れると,Haversineの公式では300m程の誤差が出てしまいます.Hubenyの公式でも約40mの誤差が出るので精度を求めるのであればこの2つの手法は限界な気がします.
いよいよ海外進出です!
東京スカイツリー(35.71007721380533, 139.81070570812608) から
イギリスのビッグベン(51.500702456806685, -0.12463613249688912) で実験してみます.
| 計算手法 | 2地点間の距離[km] | 誤差[km] | 誤差比率[%] |
|---|---|---|---|
| Haversineの公式 | 9572.17020057 | 12.89881599 | 0.1345719 |
| Hubenyの公式 | 11433.20920830 | 1848.14019174 | 19.28144 |
| 測地線航海算法 | 9585.06744435 | 0.00157221 | 0 |
| 国土地理院の方法 | 9585.069017 | 0.00000044 | 0 |
| GeographicLib | 9585.06901656 | - | - |
10000km程にもなるとHubenyの公式の誤差が無視できない程膨れ上がってしまいます.これは,先述した直角三角形がうまくつくれないため生じたと考えられます.
極地南極にも行ってみましょう♪
東京スカイツリー(35.71007721380533, 139.81070570812608) から
昭和基地🐧(-68.75128159420852, 39.933121995422866) で実験してみます.
| 計算手法 | 2地点間の距離[km] | 誤差[km] | 誤差比率[%] |
|---|---|---|---|
| Haversineの公式 | 14079.22792948 | 35.22118544 | 0.25079 |
| Hubenyの公式 | 15726.38892853 | 1682.38218 | 11.97936 |
| 測地線航海算法 | 14043.99821637 | 0.00852767 | 0 |
| 国土地理院の方法 | 14044.006744 | 0.00000004 | 0 |
| GeographicLib | 14044.00674404 | - | - |
2点間の距離は大きくなりましたが,Hubenyの公式の誤差比率が10%程落ち着きました.これは,直角三角形が子午線方向にのびる場合は直角三角形をおきやすいことに起因しています.
最後は日本の裏側ブラジルにいってみます!!
東京スカイツリー(35.71007721380533, 139.81070570812608) から
コルコバードの丘(-22.950611479037242, -43.21136119476384) で実験してみます.
| 計算手法 | 2地点間の距離[km] | 誤差[km] | 誤差比率[%] |
|---|---|---|---|
| Haversineの公式 | 18587.40774391 | 26.67355233 | 0.143709 |
| Hubenyの公式 | 21262.37856370 | 2701.64437212 | 14.55569 |
| 測地線航海算法 | 18560.75095438 | 0.0167628 | 0 |
| 国土地理院の方法 | 18560.734191 | 0.00000058 | 0 |
| GeographicLib | 18560.73419158 | - | - |
日本の裏側にいっても測地線航海算法では10m強の誤差に抑えられており,国土地理院の方法ではほとんど誤差がありません.また,Haversineの公式も実験を通して誤差比率が0.3%を超えず,実装の簡易さの割に精度が良いことがわかります.
以上の結果から,Haversineの公式は地球を球体とみなすため,一定の誤差は生じますが,比較的安定した精度が出ることがわかります.Hubenyの公式は短距離では精度が高いですが,100kmを超えてくると精度が悪くなっていきます.測地線航海算法は10000km~対蹠点付近にかけては精度が悪くなることがわかります.国土地理院の方法は安定してとても良い精度が出ますが,実装が複雑なことが難点です.
まとめ
今回は,緯度経度から2地点間の距離を求める代表的な手法をいくつか紹介し,それらの精度比較を行いました.
実験の結論としては,
- 使用できるのならGeographicLibライブラリを使うのが精度が高く,一番良い.
- 数kmまでの短距離ならHubenyの公式が高い精度を発揮できる.
- 10km~10000kmでは測地線航海算法が安定した精度を出せる.
- 10000km~では測地線航海算法よりもHaversineの公式の方が精度が良い場合がある.
基本的にGeographicLibライブラリを使用し,ライブラリが使用できない場合は距離によって手法を使い分けるのがいいと思います!
数値計算を行う上で,地球をどうモデル化するかで生じるモデル誤差,元の位置情報によるデータ誤差,各アルゴリズムで生じるアルゴリズムの誤差,そして計算を行うときに生じる打ち切り誤差やコンピュータにおける表現の限界による丸め誤差などを考慮する必要があります.また,これらの誤差は伝搬するので微小の誤差でも計算結果では大きなズレを起こす場合があります.各アルゴリズムの特徴を理解して計算量や誤差を踏まえながら適切な手法を選択することが大切ですね✨