More than 3 years have passed since last update.

Titanicデータでベイジアンネットワークを実装

Last updated at 2020-10-06Posted at 2020-09-07

先日、DeepLearningを用いたネットワーク分析手法であるSAM(Structural Agnostic Modeling)をTitanicデータで実装した記事を記載しました。
今回はネットワーク分析の最もポピュラーな手法であるベイジアンネットワークをTitanicデータで実装しましたので紹介します。

SAMの記事は以下をご参照ください。
SAMの記事

記事で紹介していないものも含めて、コードは全てGitHubに置いてあります。
https://github.com/yuomori0127/Bayesian_Network

#目次

ゴールと概要
ベイジアンネットワークとは
ベイジアンネットワークを関数で簡単に実装
最後に

#1. ゴールと概要
ネットワーク分析のゴールについては以前の記事と重複するので割愛します。
以前の記事をご参照ください。
ネットワーク分析のゴール

簡単に言うと以下のように変数間のグラフ構造を明らかにすることです。

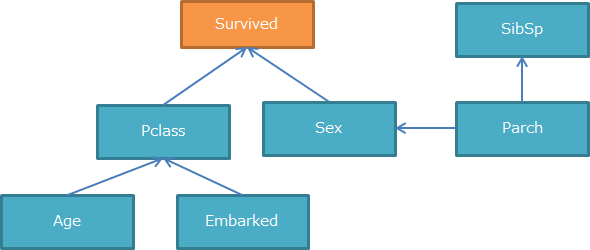
#2. ベイジアンネットワークとは
ベイジアンネットワークは条件付き確率をベースに、変数間のグラフ構造を表現したものです。

ベイジアンネットワークの中でも、依存関係(矢印)を算出する方法はいくつかあるのですが、
今回は以下の手順で実施しました。

1. 独立性の検定により、変数間のスケルトン(方向のない依存関係)を特定
2. V-structure,オリエンテーションルールにより一部のスケルトンに方向を付与
3. BICを用いて残りのスケルトンに方向を付与

1,2,はPCアルゴリズム[1]と呼ばれる方法で、
3はスコアベースアプローチと呼ばれる方法です。

#2-1. 独立性の検定
まずは下図のようなスケルトン(方向のない依存関係)を特定します。

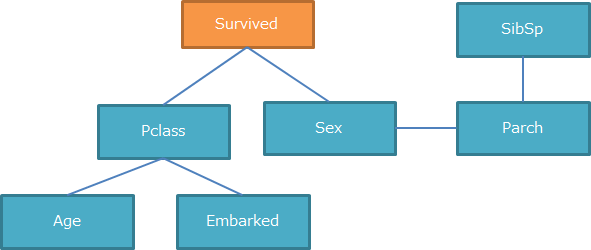
スケルトンを特定するためには独立性の検定を行います。
これはカイ二乗検定と呼ばれ、変数間に関連があるかどうかを検定するものです。
カイ二乗検定参考：https://bellcurve.jp/statistics/course/9496.html

また、単純な変数間の独立性の検定に加え、条件付き独立の検定も実施します。
これはある変数Aを条件としたとき(変数Aを固定した時)の変数B・変数C間の独立性の検定で、これを2次(条件が2変数)まで行います。

つまり、以下3つの独立性の検定を行います。

1. 0次の独立性の検定(単純な2変数間の独立性の検定)
2. 1次の独立性の検定(1変数を条件としたときの2変数間の独立性の検定)
3. 2次の独立性の検定(2変数を条件としたときの2変数間の独立性の検定)

##2-1-1. 0次の独立性の検定
言語はPythonで、ライブラリはpgmpyを使用しました。
99%有意で2変数間の検定を行います。

#0次の独立性を検定する関数定義
def independence_0(df):
  independence_list=[]
  est = ConstraintBasedEstimator(df)
  for col1,col2 in list(itertools.combinations(df.columns, 2)):
    result = est.test_conditional_independence(col1, col2, method="chi_square", tol=0.01)
    print("{}-{} -> {}".format(col1,col2,result))
    if not result:
      independence_list.append([col1,col2]) 
  return independence_list

0次の独立性検定の実行し、全変数間の検定結果を表示させています。
また、検定結果がFalseであるもの(独立ではないと判定されたもの)の一覧をindependence_list_0に格納しています。

#0次の独立性検定の実行
independence_list_0 = independence_0(df)
# 実行結果
# Survived-Pclass -> False
# Survived-Sex -> False
# Survived-Age -> True
# Survived-SibSp -> False
# 以下略

検定結果がFalseであるもの(=独立ではない変数)同士を繋げて可視化すると以下のようになりました。

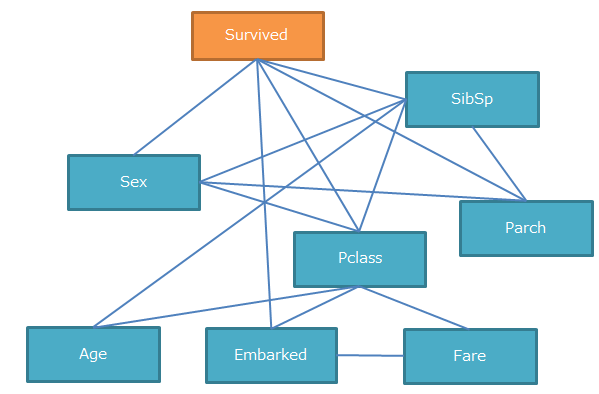
相当ごちゃごちゃしています。。

ここから1次、2次の独立性の検定を行い、変数間の関係性をさらに見ていきます。

##2-1-2. 1次、2次の独立性の検定
1次の独立性の検定とは、ある1つの変数を条件付きにした際(1つの変数の値を固定した際)の2つの変数間の独立性の検定です。
コードは長くなるのでGitHubに置いてあります。

1次の独立性の検定の結果、以下のようになりました。

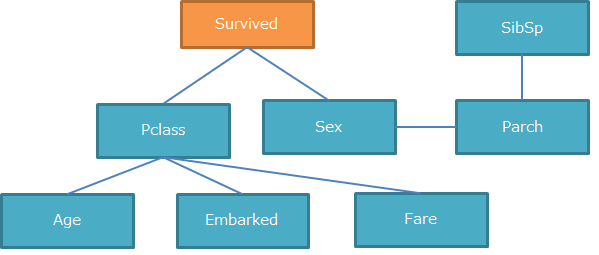
相当スッキリしました。

同様に2次の独立性の検定も実施し、以下のようになりました。

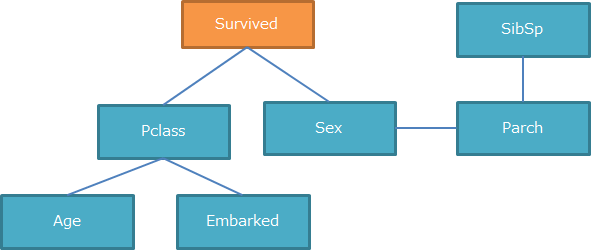
右下の「Fare」が消えました。
これでスケルトンは完成です。
次はこの図に方向を付与していきます。

#2-2. V-structure,オリエンテーションルール
スケルトンに方向を付与する手段として、V-structure,オリエンテーションルールの2つを実施します。

#2-2-1. V-structure
V-structureとは文字通り、V字構造を持った変数間の関係性を指します。

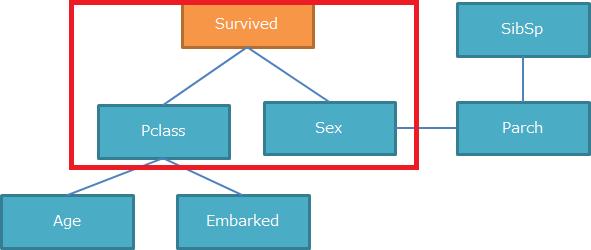
この時、V字の中心(例では「Survived」)を条件に置き、残りの2つの変数(例では「Pclass」と「Sex」)間で独立性が無ければ、以下の矢印を付与することができます。

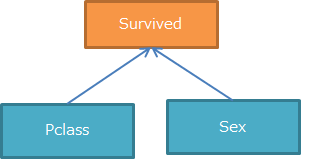
これはつまり、「Pclass」と「Sex」が決まれば「Survived」も決まりやすい関係にあることを意味します。

このように、V字構造を持つ全ての組み合わせに対して条件付き独立性の検定を行います。
こちらも99%有意で検定しています。

# V-structureの探索(条件付き非独立の場合、連結できる)
#①Pclass-Survived-Sex
print(est.test_conditional_independence(
    'Pclass', 'Sex', ['Survived'], method="chi_square", tol=0.01))

#②Age-Pclass-Embarked
print(est.test_conditional_independence(
    'Age', 'Embarked', ['Pclass'], method="chi_square", tol=0.01))

#③Survived-Sex-Parch
print(est.test_conditional_independence(
    'Survived', 'Parch', ['Sex'], method="chi_square", tol=0.01))

#④Sex-Parch-SibSp
print(est.test_conditional_independence(
    'Sex', 'SibSp', ['Parch'], method="chi_square", tol=0.01))

# 実行結果
# False
# True
# True
# True

検定の結果、①Pclass-Survived-Sex間のみFalseとなり、**独立ではない(=関係性がある)**という結果となりました。
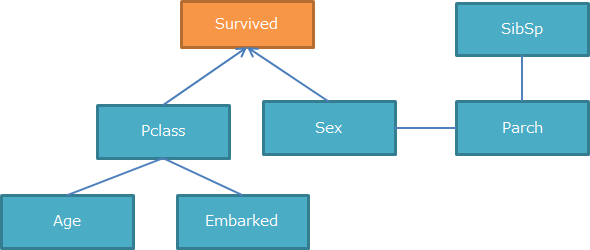
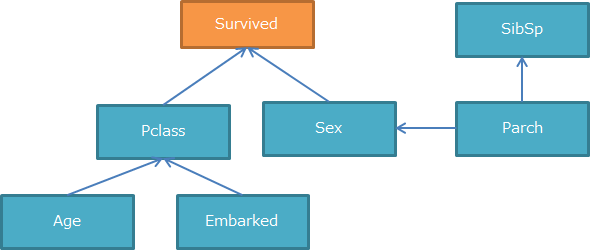
そのため①Pclass-Survived-Sex間に矢印が付与され、図は以下のようになります。

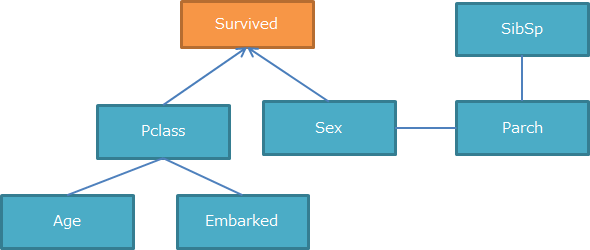
#2-2-2. オリエンテーションルール
V-structureを含む部分的な矢印が得られている場合、付加的に矢印の向きを決定できることがあります。
このルールをオリエンテーションルール[3]と呼びます。

以下のパターンの場合、付加的に矢印の向きを決定することができます。[3]

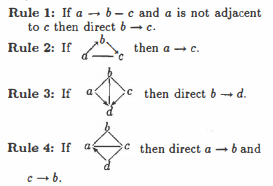
今回の例ではオリエンテーションルールにあてはまる構造がないため、図は変わりません。

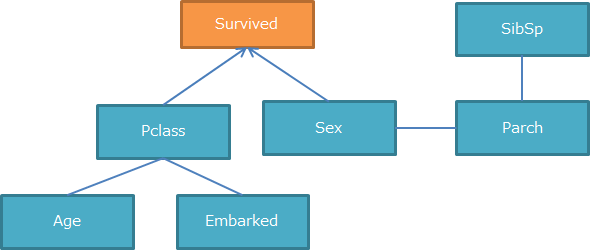
#2-3. スコアベースアプローチ(BIC)
残りのスケルトンに対して矢印を決定する方法として、
BICによるスコアベースアプローチを考えます。

BICの詳細説明は省略します。以下の文献をご参考ください。

[4]「作りながら学ぶ！Pythonによる因果分析」(小川雄太郎著 2020)
WikiPedia

要はグラフィカルモデルの評価指標です。

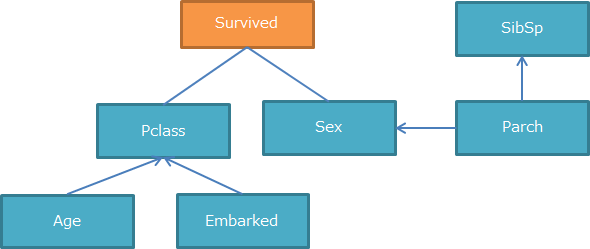
下図でスケルトンとなっている線は4本ありますが、
そのすべてに対して2方向の矢印を仮定した場合、 $ 2^4=16 $ 通りのグラフィカルモデルが考えられます。
その16パターン全てをBICで評価し、最も評価値が高いものを採用するという方法で残りのスケルトンに対して矢印を決定していきます。

16パターン全てをここには記載しませんが、
最も評価が高いもので約-4936.9となりました。(BICはマイナスが大きい方が良いモデル)

model = BayesianModel([('Pclass', 'Survived'), ('Sex', 'Survived'),('Age', 'Pclass'), ('Embarked', 'Pclass'),('Sex', 'Parch'), ('SibSp', 'Parch')])  
print(BicScore(df).score(model))
# 実行結果
# -4936.911652064051

最もBICでの評価が高いモデルは下図となりました。

#3. ベイジアンネットワークを関数で簡単に実装
今まで色々実施してきましたが、実は似たようなことを簡単に実施する関数が存在します。

est = ConstraintBasedEstimator(df)

skel, seperating_sets = est.estimate_skeleton(significance_level=0.01)
print("Undirected edges: ", skel.edges())

pdag = est.skeleton_to_pdag(skel, seperating_sets)
print("PDAG edges:       ", pdag.edges())

model = est.pdag_to_dag(pdag)
print("DAG edges:        ", model.edges())
# 実行結果
# Undirected edges:  [('Survived', 'Pclass'), ('Survived', 'Sex'), ('Pclass', 'Age'), ('Pclass', 'Embarked'), ('Sex', 'Parch'), ('SibSp', 'Parch')]
# PDAG edges:        [('Age', 'Pclass'), ('SibSp', 'Parch'), ('Parch', 'Sex'), ('Parch', 'SibSp'), ('Embarked', 'Pclass')]
# DAG edges:         [('Age', 'Pclass'), ('Parch', 'Sex'), ('Parch', 'SibSp'), ('Embarked', 'Pclass')]

下から3つ目のUndirected edgesは方向性なし
下から2つ目のPDAG edgesは部分的な方向性あり
一番下のDAG edgesは方向性あり

を意味します。

これらをもとに図を描くと以下のようになります。

「Survived」のみ方向性がないですが、それ以外は全く同じ結果となりました。
このことからどちらの方法でもある程度同じ結果が得られることがわかります。
試しにBICを算出してみます。

model = BayesianModel([('Age', 'Pclass'), ('Embarked', 'Pclass'),('Sex', 'Parch'), ('SibSp', 'Parch')])  
print(BicScore(df).score(model))

# 実行結果
# -4517.5517518749075

先程のモデルは約-4936.9だったので、今回の方がBICの絶対値が小さいです。
なので、「Survived」への矢印はあった方が良いことがわかります。

#4. 最後に
今回、Titanicデータでベイジアンネットワークを実装しました。
相当簡単に実装できる関数も存在しますし、BICによる評価も簡単にできるため、
関数により作成したモデルに業務観点で手動で依存関係(矢印)を入れてみて評価してみる、みたいなこともできます。
是非実施してみてください。

#参考文献
[1] Spirtes, P., Glymour, C., & Scheines, R. (2000). Causation, Prediction, and Search
[2] 「統計WEB 25-5. 独立性の検定」 https://bellcurve.jp/statistics/course/9496.html
[3] Tom S. Verma, Judea Pearl."An Algorithm for Deciding if a Set of Observed Independencies Has a Causal Explanation" https://arxiv.org/abs/1303.5435 (2013)
[4] 「作りながら学ぶ！Pythonによる因果分析」(小川雄太郎著 2020)
[5] 「効果検証入門」(安井翔太著 2020)

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up