#Pythonで学ぶアルゴリズム< 迷路探索 >
はじめに
基本的なアルゴリズムをPythonで実装し,アルゴリズムの理解を深める.
その第12弾として迷路探索を扱う.
迷路の定義
ここでは,次のような2次元迷路を扱う.
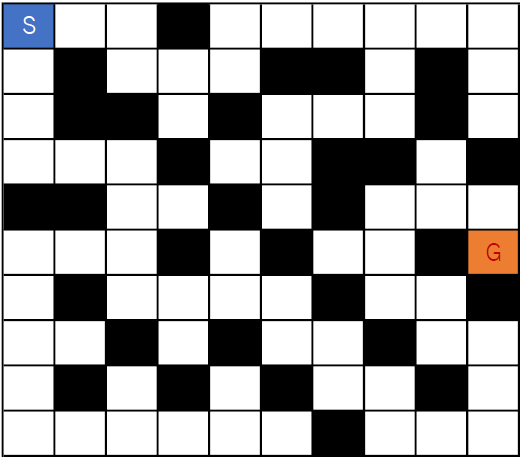
S, Gはそれぞれスタートとゴールを示す.また黒塗は壁で,通過可能なのは白塗のマスのみとする.
さらに,プログラムで扱うため,スタート,ゴール,壁,道に次のように数字を対応付けさせる.
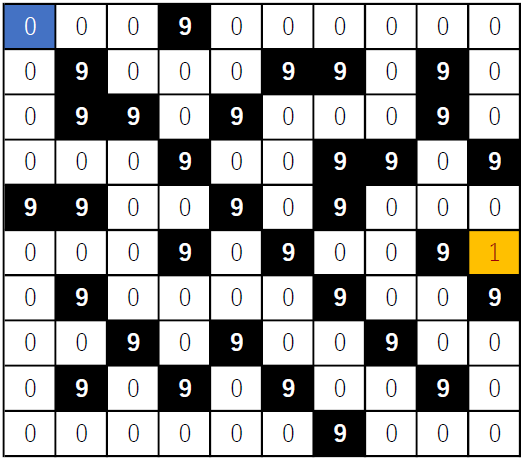
また,探索途中通過した道は数字を2に上書きする.
今回は番兵を用いて,幅優先探索と深さ優先探索2つの方法で迷路探索を行う.
番兵とは
番兵とは終了条件としてリストに付加するデータのことである.今回でいう番兵は上記の図にはない外壁の存在である.10×10の迷路であるが,プログラムで表現する時には外壁を考慮して12×12の迷路となる.これにより,内壁,外壁を区別することなく,進めない場所の判定が可能になる.このように単純化させることができるのが番兵の効果である.
実装
上記の条件を踏まえて,迷路探索を行う.プログラムは幅優先探索,深さ優先探索の順にそのコードと出力を示す.
コード(幅優先探索)
"""
2020/12/30
@Yuya Shimizu
番兵
迷路探索1(幅優先探索)
"""
# 探索関数:ゴールしたらそのときの位置・移動数を返す
def Maze(start):
#スタート位置(x座標, y座標, 移動回数)をセット
pos = start
while len(pos) > 0:#探索可能ならTrue
x, y, depth = pos.pop(0) #リストから探索する位置を取得
#ゴールについた時点で終了
if maze[x][y] == 1:
return [(x, y), depth]
#探索済みとしてセット
maze[x][y] = 2
#現在位置の上下左右を探索:〇<2は壁でもなく探索済みでもないものを示す
if maze[x-1][y] < 2:#左
pos.append([x-1, y, depth + 1])
if maze[x+1][y] < 2:#右
pos.append([x+1, y, depth + 1])
if maze[x][y-1] < 2:#上
pos.append([x, y-1, depth + 1])
if maze[x][y+1] < 2:#下
pos.append([x, y+1, depth + 1])
return False
if __name__ == '__main__':
#迷路作成
maze = [
[9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9],
[9, 0, 0, 0, 9, 0, 0, 0, 0, 0, 0, 9],
[9, 0, 9, 0, 0, 0, 9, 9, 0, 9, 0, 9],
[9, 0, 9, 9, 0, 9, 0, 0, 0, 9, 0, 9],
[9, 0, 0, 0, 9, 0, 0, 9, 9, 0, 9, 9],
[9, 9, 9, 0, 0, 9, 0, 9, 0, 0, 0, 9],
[9, 0, 0, 0, 9, 0, 9, 0, 0, 9, 1, 9],
[9, 0, 9, 0, 0, 0, 0, 9, 0, 0, 9, 9],
[9, 0, 0, 9, 0, 9, 0, 0, 9, 0, 0, 9],
[9, 0, 9, 0, 9, 0, 9, 0, 0, 9, 0, 9],
[9, 0, 0, 0, 0, 0, 0, 9, 0, 0, 0, 9],
[9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9]
]
start = [[1, 1, 0]] #スタート位置
result = Maze(start) #探索
print(result)
出力
[(6, 10), 28]
出力は(x, y)座標と移動回数である.
次に,その探索の様子を出力するコードを示す.出力は非常に長くなってしまうため一部のみ示す.
コード(可視化)
"""
2020/12/30
@Yuya Shimizu
番兵
迷路探索1(幅優先探索)
"""
from time import sleep
# 探索様子を追跡する関数(迷路の更新を出力する)
def track(maze, start, depth):
draw = f"{depth}手目\n"
for x in range(len(maze)):
for y in range(len(maze[x])):
if x == start[0][0] and y == start[0][1]:
draw += "S " #スタート位置
elif maze[x][y] > 2:
draw += "■ " #壁
elif maze[x][y] == 2:
draw += "* " #探索済みの道
elif maze[x][y] == 1:
draw += "G " #ゴール位置
else:
draw += " " #未探索の道
draw += "\n"
print(draw)
# 探索関数:ゴールしたらそのときの位置・移動数を返す
def Maze(start):
#スタート位置(x座標, y座標, 移動回数)をセット
pos = start.copy()
while len(pos) > 0:#探索可能ならTrue
x, y, depth = pos.pop(0) #リストから探索する位置を取得
#ゴールについた時点で終了
if maze[x][y] == 1:
return [(x, y), depth]
#探索済みとしてセット
maze[x][y] = 2
#1秒ごとに図の更新
sleep(1)
track(maze, start, depth)
#現在位置の上下左右を探索:〇<2は壁でもなく探索済みでもないものを示す
if maze[x-1][y] < 2:#左
pos.append([x-1, y, depth + 1])
if maze[x+1][y] < 2:#右
pos.append([x+1, y, depth + 1])
if maze[x][y-1] < 2:#上
pos.append([x, y-1, depth + 1])
if maze[x][y+1] < 2:#下
pos.append([x, y+1, depth + 1])
return False
if __name__ == '__main__':
#迷路作成
maze = [
[9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9],
[9, 0, 0, 0, 9, 0, 0, 0, 0, 0, 0, 9],
[9, 0, 9, 0, 0, 0, 9, 9, 0, 9, 0, 9],
[9, 0, 9, 9, 0, 9, 0, 0, 0, 9, 0, 9],
[9, 0, 0, 0, 9, 0, 0, 9, 9, 0, 9, 9],
[9, 9, 9, 0, 0, 9, 0, 9, 0, 0, 0, 9],
[9, 0, 0, 0, 9, 0, 9, 0, 0, 9, 1, 9],
[9, 0, 9, 0, 0, 0, 0, 9, 0, 0, 9, 9],
[9, 0, 0, 9, 0, 9, 0, 0, 9, 0, 0, 9],
[9, 0, 9, 0, 9, 0, 9, 0, 0, 9, 0, 9],
[9, 0, 0, 0, 0, 0, 0, 9, 0, 0, 0, 9],
[9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9]
]
start = [[1, 1, 0]] #スタート位置
result = Maze(start) #探索
print(result)
出力
12手目
■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■
■ S * * ■ * * * * * * ■
■ * ■ * * * ■ ■ * ■ ■
■ * ■ ■ * ■ * ■ ■
■ * * * ■ ■ ■ ■ ■
■ ■ ■ * * ■ ■ ■
■ * * * ■ * ■ ■ G ■
■ * ■ * * * * ■ ■ ■
■ * * ■ * ■ * ■ ■
■ * ■ ■ ■ ■ ■
■ ■ ■
■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■
環境の違いや,改行により,少し縦長に見えるがプログラムを実際に実行するともう少しましな図となる.参考にそのときのスクリーンショットを以下に示す.

コード(深さ優先探索)
"""
2020/12/30
@Yuya Shimizu
番兵
迷路探索2(単純な深さ優先探索)
"""
# 探索関数:ゴールしたらそのときの位置・移動数を返す
def Maze(x, y, depth):
#ゴールについた時点で終了
if maze[x][y] == 1:
print([(x, y), depth])
#探索済みとしてセット
maze[x][y] = 2
#現在位置の上下左右を探索:〇<2は壁でもなく探索済みでもないものを示す
if maze[x-1][y] < 2:#左
Maze(x-1, y, depth + 1)
if maze[x+1][y] < 2:#右
Maze(x+1, y, depth + 1)
if maze[x][y-1] < 2:#上
Maze(x, y-1, depth + 1)
if maze[x][y+1] < 2:#下
Maze(x, y+1, depth + 1)
#探索前に戻す
maze[x][y] = 0
if __name__ == '__main__':
#迷路作成
maze = [
[9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9],
[9, 0, 0, 0, 9, 0, 0, 0, 0, 0, 0, 9],
[9, 0, 9, 0, 0, 0, 9, 9, 0, 9, 0, 9],
[9, 0, 9, 9, 0, 9, 0, 0, 0, 9, 0, 9],
[9, 0, 0, 0, 9, 0, 0, 9, 9, 0, 9, 9],
[9, 9, 9, 0, 0, 9, 0, 9, 0, 0, 0, 9],
[9, 0, 0, 0, 9, 0, 9, 0, 0, 9, 1, 9],
[9, 0, 9, 0, 0, 0, 0, 9, 0, 0, 9, 9],
[9, 0, 0, 9, 0, 9, 0, 0, 9, 0, 0, 9],
[9, 0, 9, 0, 9, 0, 9, 0, 0, 9, 0, 9],
[9, 0, 0, 0, 0, 0, 0, 9, 0, 0, 0, 9],
[9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9]
]
result = Maze(1, 1, 0) #探索
出力
[(6, 10), 28]
出力は(x, y)座標と移動回数である.
次に,その探索の様子を出力するコードを示す.出力は非常に長くなってしまうため一部のみ示す.
コード(可視化)
"""
2020/12/30
@Yuya Shimizu
番兵
迷路探索2(単純な深さ優先探索)
"""
from time import sleep
# 探索様子を追跡する関数(迷路の更新を出力する)
def track(maze, depth):
draw = f"{depth}手目\n"
for x in range(len(maze)):
for y in range(len(maze[x])):
if maze[x][y] > 2:
draw += "■ " #壁
elif maze[x][y] == 2:
draw += "* " #探索済みの道
elif maze[x][y] == 1:
draw += "G " #ゴール位置
else:
draw += " " #未探索の道
draw += "\n"
print(draw)
# 探索関数:ゴールしたらそのときの位置・移動数を返す
def Maze(x, y, depth):
#ゴールについた時点で終了
if maze[x][y] == 1:
print([(x, y), depth])
exit()
#探索済みとしてセット
maze[x][y] = 2
#1秒ごとに図の更新
sleep(1)
track(maze, depth)
#現在位置の上下左右を探索:〇<2は壁でもなく探索済みでもないものを示す
if maze[x-1][y] < 2:#左
Maze(x-1, y, depth + 1)
if maze[x+1][y] < 2:#右
Maze(x+1, y, depth + 1)
if maze[x][y-1] < 2:#上
Maze(x, y-1, depth + 1)
if maze[x][y+1] < 2:#下
Maze(x, y+1, depth + 1)
#探索前に戻す
maze[x][y] = 0
if __name__ == '__main__':
#迷路作成
maze = [
[9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9],
[9, 0, 0, 0, 9, 0, 0, 0, 0, 0, 0, 9],
[9, 0, 9, 0, 0, 0, 9, 9, 0, 9, 0, 9],
[9, 0, 9, 9, 0, 9, 0, 0, 0, 9, 0, 9],
[9, 0, 0, 0, 9, 0, 0, 9, 9, 0, 9, 9],
[9, 9, 9, 0, 0, 9, 0, 9, 0, 0, 0, 9],
[9, 0, 0, 0, 9, 0, 9, 0, 0, 9, 1, 9],
[9, 0, 9, 0, 0, 0, 0, 9, 0, 0, 9, 9],
[9, 0, 0, 9, 0, 9, 0, 0, 9, 0, 0, 9],
[9, 0, 9, 0, 9, 0, 9, 0, 0, 9, 0, 9],
[9, 0, 0, 0, 0, 0, 0, 9, 0, 0, 0, 9],
[9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9]
]
result = Maze(1, 1, 0) #探索
出力
27手目
■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■
■ * ■ ■
■ * ■ ■ ■ ■ ■
■ * ■ ■ ■ ■ ■
■ * * * ■ ■ ■ ■ ■
■ ■ ■ * ■ ■ * * * ■
■ * ■ ■ * ■ G ■
■ ■ * * * * ■ * * ■ ■
■ ■ ■ * * ■ * * ■
■ ■ ■ ■ * * ■ * ■
■ ■ * * * ■
■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■
[(6, 10), 28]
同様に,環境の違いや,改行により,少し縦長に見えるがプログラムを実際に実行するともう少しましな図となる.参考にそのときのスクリーンショットを以下に示す.

感想
迷路探索を学んだ.これは移動ロボットにおける探索に通ずるところがあると勉強しているときに思った.本書では右手法についても載っていた.右手法については今回記述していないが,理解することはできた.また,前回の木構造の例の1つであるため,その木構造探索の応用を通して,より深い理解が得られたと思う.
探索に関する例はもう少し触れる予定である.今回はその第1弾であった.
参考文献
Pythonで始めるアルゴリズム入門 伝統的なアルゴリズムで学ぶ定石と計算量
増井 敏克 著 翔泳社