#Javaで学ぶアルゴリズム < 乱数 >
はじめに
Javaは授業で触れただけで全くの初心者であり,何もわかっていない.なので,基本的なアルゴリズムをJavaで実装し,アルゴリズムの理解を深めるとともに,Javaにも慣れていきたい.
その第7弾として乱数を扱う.
乱数
意味としては無作為に得られるランダムな数値であるが,コンピュータ言語にある乱数発生ライブラリはすべて擬似乱数と呼ばれる計算によって求められる乱数である.ここでは,その発生方法の仕組みや,評価も実装を通して学ぶ.なお,その2つは一様乱数(線形合同法)とボックス・ミュラー法である.
一様乱数(線形合同法)
実装
以下にソースコードとそのときの出力を示す.
ソースコード: 一様乱数(線形合同法)
//2021/02/16
//@Yuya Shimizu
//-------------------------------
//* 一様乱数(線形合同法) *
//-------------------------------
import java.awt.*;
import java.awt.event.*;
//パネルの設定
class uniform_random_Panel extends Panel{
int rndnum = 13; //線形合同法で用いる初期値
int irnd() {
//0~32767の整数乱数
rndnum = (rndnum * 109 + 1021) % 32768;//線形合同法
return rndnum;
}
public void paint(Graphics g){
int i, y=1;
g.drawString("求められた一様乱数", 0, 20);//(0, 20)の座標に"求められた一様乱数"をセット
//8行並べたら改行するためyの値
for (i=0; i<100; i++){
if (i%8 == 0){
y++;
}
g.drawString("" + irnd(), (i%8)*60, y*20);
}
}
}
//フレームの設定
class uniform_random_Frame extends Frame{
public uniform_random_Frame(){
setSize(500, 350);//500×350の大きさでフレームを作成
//×ボタンを押したら終了
addWindowListener(new WindowAdapter(){
public void windowClosing(WindowEvent e){
System.exit(0);
}
});
Panel p=new uniform_random_Panel();//パネルオブジェクトpに先ほど設定したパネルを指定
add(p); //フレームにそのパネルを貼り付け
}
}
//クラス
public class uniform_random_numbers{
//メイン関数
public static void main(String[] args){
Frame w=new uniform_random_Frame();
w.show();
}
}
出力
χ2検定
先ほどの一様乱数の散らばり具合を調べる.簡単な説明を示した後,実装を行う.

実装
以下にソースコードとそのときの出力を示す.
ソースコード: χ2検定
//2021/02/16
//@Yuya Shimizu
//-------------------------------
//* 一様性の検定(χの2乗) *
//-------------------------------
import java.awt.*;
import java.awt.event.*;
//パネルの設定
class test_Panel extends Panel{
int rndnum = 13; //線形合同法で用いる初期値
int irnd() {
//0~32767の整数乱数
rndnum = (rndnum * 109 + 1021) % 32768;//線形合同法
return rndnum;
}
//0~1未満の整数乱数を生成する関数
double rnd(){
return irnd()/32767.1;
}
public void paint(Graphics g){
final int N = 1000, //乱数の発生回数
M = 10, //整数乱数の範囲
F = N/M; //期待値
final double SCALE = 20.0/F; //ヒストグラムの高さ(自動スケール)
int i, j, rank;
int [] hist = new int[M+1];
double e = 0.0;
for (i=1; i<=M; i++){
hist[i] = 0;
}
for (i=0; i<N; i++){
rank = (int)(M*rnd() + 1);
hist[rank]++;
}
String dot;
g.drawString("一様の検定", 0, 20); //(0, 20)の座標に"一様の検定"をセット
//ヒストグラムの表示
for (i=1; i<=M; i++){
dot = "";
for (j=0; j<hist[i]*SCALE; j++)
dot = dot + "■";
g.drawString("" + i + ":" + hist[i], 0, i*20+20);
g.drawString(dot, 40, i*20+20);
e = e + (double)(hist[i] - F) * (hist[i] - F)/F;
}
g.drawString("χ^2=" + e, 0, (i+1)*20);//χ^2の計算
}
}
//フレームの設定
class test_Frame extends Frame{
public test_Frame(){
setSize(500, 300);//500×300の大きさでフレームを作成
//×ボタンを押したら終了
addWindowListener(new WindowAdapter(){
public void windowClosing(WindowEvent e){
System.exit(0);
}
});
Panel p=new test_Panel();//パネルオブジェクトpに先ほど設定したパネルを指定
add(p); //フレームにそのパネルを貼り付け
}
}
//クラス
public class test_uniformity{
//メイン関数
public static void main(String[] args){
Frame w=new test_Frame();
w.show();
}
}
出力

$\chi ^2$の値が約2ということは,各要素に対する2乗誤差割合の総和が2ほど,つまり平均して,期待値との誤差が約2であるという結果ということで,そこそこ一様に散らばっているのではないだろうか.実際に,期待値100に対して,上図に示された各要素のずれを平均すると,
$(+1) + (-2) + (-4) + (+7) + (\pm0) + (-6) + (+1) + (+4) + (+6) + (-7) = 2$
となり,$\chi ^2$が約2という意味が分かった.
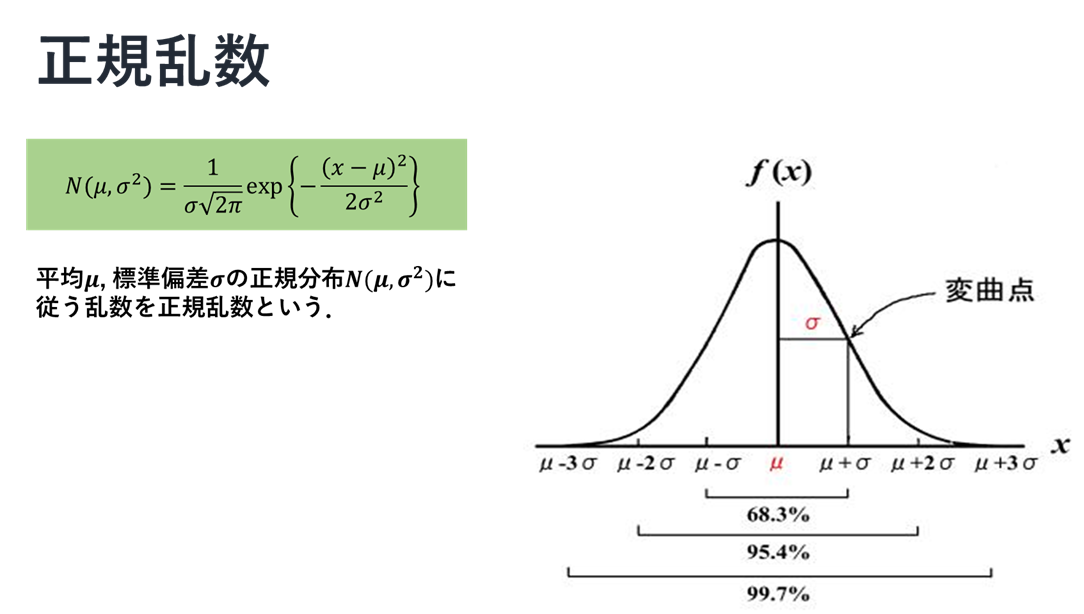
正規乱数(ボックス・ミュラー法)
正規乱数についての説明の後,ボックス・ミュラー法を説明し,その後に実装を行う.

実装
以下にソースコードとそのときの出力を示す.
ソースコード: 正規乱数(ボックス・ミュラー法)
//2021/02/16
//@Yuya Shimizu
//-------------------------------------------
//* 正規乱数(ボックス・ミュラー法) *
//-------------------------------------------
import java.awt.*;
import java.awt.event.*;
//パネルの設定
class normal_random_Panel extends Panel{
//ボックス・ミュラー法を適用する関数
void brnd(double sig, double m, double[] r) {
double r1, r2;
r1 = Math.random();
r2 = Math.random();
r[0] = sig * Math.sqrt(-2*Math.log(r1)) * Math.cos(2*3.14159 * r2) + m;
r[1] = sig * Math.sqrt(-2*Math.log(r1)) * Math.sin(2*3.14159 * r2) + m;
}
//結果を描画する関数
public void paint(Graphics g){
int i, j;
int[] hist = new int[100];
double[] r = new double[2]; //乱数を得る引数配列
for (i=0; i<100; i++){
hist[i] = 0;
}
for (i=0; i<1000; i++){
brnd(2.5, 10.0, r);
hist[(int)r[0]]++;
hist[(int)r[1]]++;
}
String dot;
g.drawString("正規乱数", 0, 20); //(0, 20)の座標に"一様の検定"をセット
//ヒストグラムの表示
for (i=0; i<=20; i++){
dot = "";
for (j=1; j<hist[i]/10; j++)
dot = dot + "■";
g.drawString("" + i, 0, i*16+40);
g.drawString(": I" + dot, 30, i*16+40);
}
}
}
//フレームの設定
class normal_random_Frame extends Frame{
public normal_random_Frame(){
setSize(500, 400);//500×400の大きさでフレームを作成
//×ボタンを押したら終了
addWindowListener(new WindowAdapter(){
public void windowClosing(WindowEvent e){
System.exit(0);
}
});
Panel p=new normal_random_Panel();//パネルオブジェクトpに先ほど設定したパネルを指定
add(p); //フレームにそのパネルを貼り付け
}
}
//クラス
public class normal_random_numbers{
//メイン関数
public static void main(String[] args){
Frame w=new normal_random_Frame();
w.show();
}
}
出力
横から見ると,確かに正規分布のような形をしている.
その他
コンピュータの乱数は一様乱数が基本となっている.
一様乱数を用いて,正規乱数に加えて,二項乱数,ポアソン乱数,指数乱数,ワイブル乱数,ガンマ乱数などの各種乱数を作ることができる.
感想
今回は,今までなんとなくプログラミングの中で使ってきていた乱数の仕組みについて学ぶことができた.また,$\chi ^2$検定により一様性を確認する中で,$\chi ^2$検定についての理解も深められたと思う.
参考文献
Javaによるはじめてのアルゴリズム入門 河西 朝雄 著 技術評論社