#Pythonで学ぶ制御工学< 時間応答(1次遅れ系) >
はじめに
基本的な制御工学をPythonで実装し,復習も兼ねて制御工学への理解をより深めることが目的である.
その第8弾として「時間応答(1次遅れ系)」を扱う.
時間応答(1次遅れ系)
時間応答の1次遅れ系について,図を使っての説明を以下に示す.
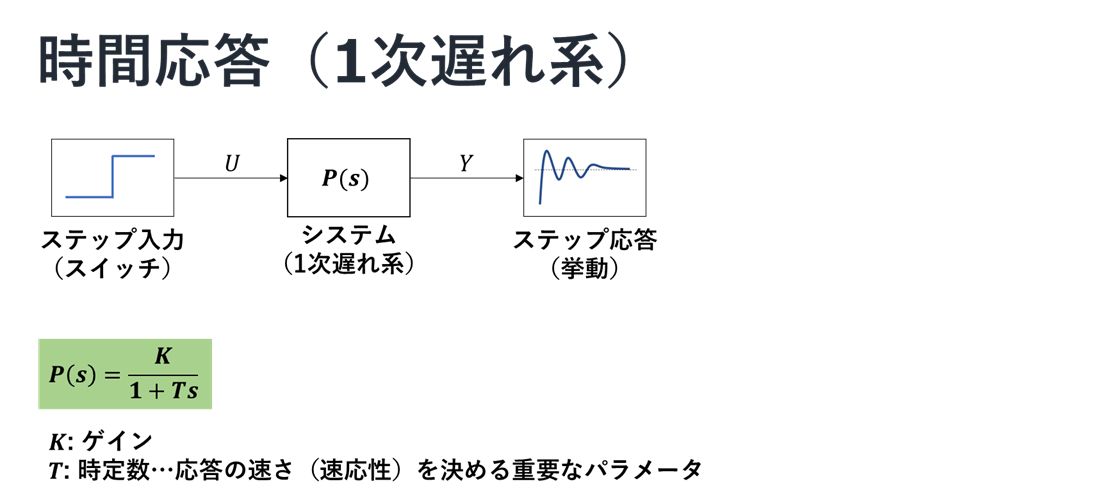
このようにして,1次遅れ系の形にした時に,対応する部分がゲインおよび時定数となる.
実装
ここでは,適当なゲインと時定数を指定し,ステップ応答の図を出力するプログラムを実装する.なお,出力する図は3つあり,ステップ応答・時定数を変化させたステップ応答・ゲインを変化させたステップ応答である.
ソースコード
"""
2021/02/26
@Yuya Shimizu
時間応答(1次遅れ系)
"""
from control.matlab import *
import matplotlib.pyplot as plt
import numpy as np
from for_plot import * #自分で定義した関数をインポート
# 定義した関数について (https://qiita.com/Yuya-Shimizu/items/f811317d733ee3f45623)
## 1次遅れ系のステップ応答
T, K = 0.5, 1 #時定数とゲインの設定
P = tf([0, K], [T, 1]) #1次遅れ系
y, t = step(P, np.arange(0, 5, 0.01)) #ステップ応答(0~5秒で,0.01刻み)
fig1, ax1 = plt.subplots()
ax1.plot(t, y)
plot_set(ax1, 't', 'y') #グリッドやラベルを与える関数(自作のfor_plotライブラリより)
plt.title(f"T={T}, K={K}")
plt.show()
## 1次遅れ系のステップ応答(時定数Tを変化させる)
K = 1
T = (1, 0.5, 0.1) #3種類の時定数を用意
# 図示の準備
fig2, ax2 = plt.subplots()
LS = linestyle_generator() #線種を与える関数(自作のfor_plotライブラリより)
for i in range(len(T)):
P = tf([0, K], [T[i], 1]) #1次遅れ系
y, t = step(P, np.arange(0, 5, 0.01)) #ステップ応答(0~5秒で,0.01刻み)
ax2.plot(t, y, ls=next(LS), label=f"T={T[i]}")
plot_set(ax2, 't', 'y', 'best')
plt.title(f"T={T}, K={K}")
plt.show()
## 1次遅れ系のステップ応答(ゲインKを変化させる)
T = 0.5
K = (1, 2, 3) #3種類のゲインを用意
# 図示の準備
fig3, ax3 = plt.subplots()
LS = linestyle_generator() #線種を与える関数(自作のfor_plotライブラリより)
for i in range(len(K)):
P = tf([0, K[i]], [T, 1]) #1次遅れ系
y, t = step(P, np.arange(0, 5, 0.01)) #ステップ応答(0~5秒で,0.01刻み)
ax3.plot(t, y, ls=next(LS), label=f"K={K[i]}")
plot_set(ax3, 't', 'y', 'best')
plt.title(f"T={T}, K={K}")
plt.show()
出力①:ステップ応答
出力②:時定数を変化させたステップ応答
出力③:ゲインを変化させたステップ応答
結果
定常値の**63.2%**に到達する時間が時定数.すなわち,時定数Tを小さくすると応答が早くなり,逆に大きくすると応答が遅くなることが予想できる.実際に上での図からも分かる.Tが小さいほど,早く収束している.また,図に示してはないが,Tを負値にすると,一定値に収束せず,発散してしまう.ゲインKは定常値を変化させる.なぜなら,最終値の定理より,次の式が成り立つからである.
$lim_{t->\infty}\ y(t) = lim_{s->0}\ sY(s)$
$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = lim_{s->0}\ s\frac{K}{1+Ts}\frac{1}{s}$
$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = lim_{s->0}\ \frac{K}{1+Ts}$
$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = K$
追加
ソースコード:部分分数分解
"""
2021/02/26
@Yuya Shimizu
部分分数分解
"""
import sympy as sp
sp.init_printing()
s = sp.Symbol('s')
T = sp.Symbol('T', real=True)
P = 1/((1 + T*s)*s)
Apart = sp.apart(P, s)#部分分数分解
print(f"{P}\n ↓\n{Apart}")
出力
1/(s*(T*s + 1))
↓
-T/(T*s + 1) + 1/s
ソースコード:逆ラプラス変換
"""
2021/02/26
@Yuya Shimizu
逆ラプラス変換
"""
import sympy as sp
sp.init_printing()
s = sp.Symbol('s')
t = sp.Symbol('t', positive=True)
T = sp.Symbol('T', real=True)
P = 1/((1 + T*s)*s)
Inverse = sp.inverse_laplace_transform(1/s - 1/(s+1/T), s, t) #逆ラプラス変換
print(f"1/s - 1/(s+1/T)\n ↓\n{Inverse}")
出力
1/s - 1/(s+1/T)
↓
1 - exp(-t/T)
感想
時間応答が何たるかを学んだ.今回は1次遅れ系ということで,時定数やゲインの意味と特徴を知り,また時定数やゲインが制御対象によって中身は変わるということを知った.またPythonでの実装を通して,グラフでの意味のとらえ方にも触れることができた.
参考文献
Pyhtonによる制御工学入門 南 祐樹 著 オーム社