Pythonで学ぶ制御工学 第22弾：位相進み遅れ補償

#Pythonで学ぶ制御工学< 位相進み遅れ補償 >

はじめに

基本的な制御工学をPythonで実装し，復習も兼ねて制御工学への理解をより深めることが目的である．
その第22弾として「位相進み遅れ補償」を扱う．

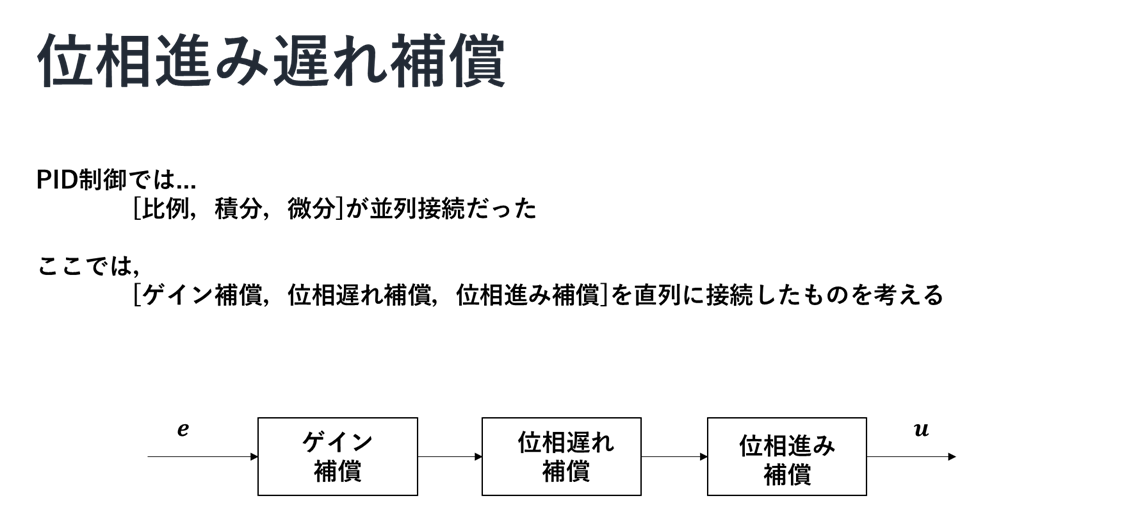
位相進み遅れ補償

以下に位相進み遅れ補償についてまとめたものを示す．

以下ではさらに詳しく位相遅れ補償と位相進み補償について示す．

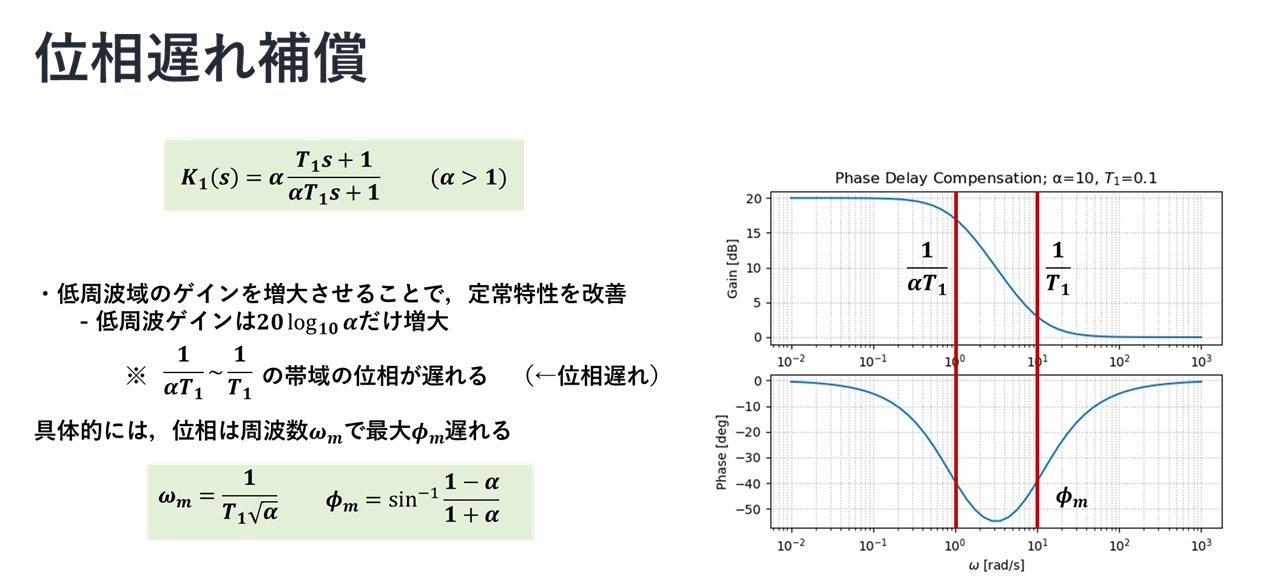
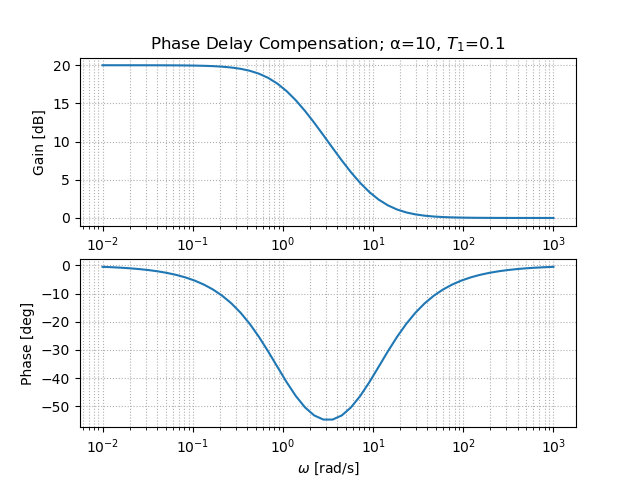
位相遅れ補償

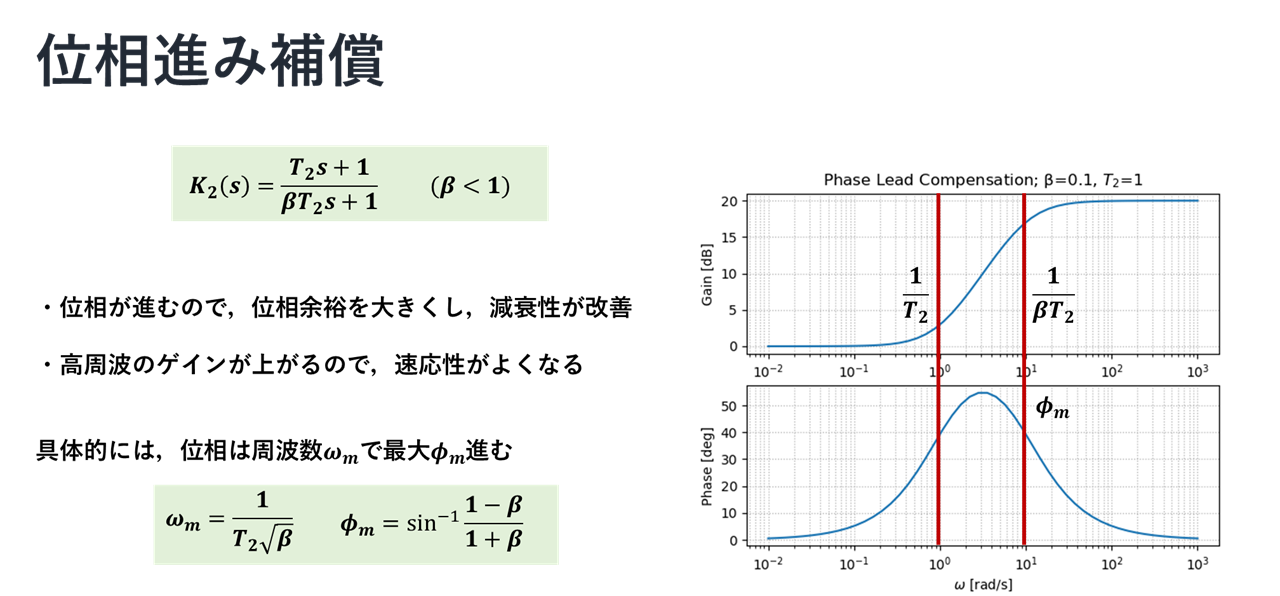
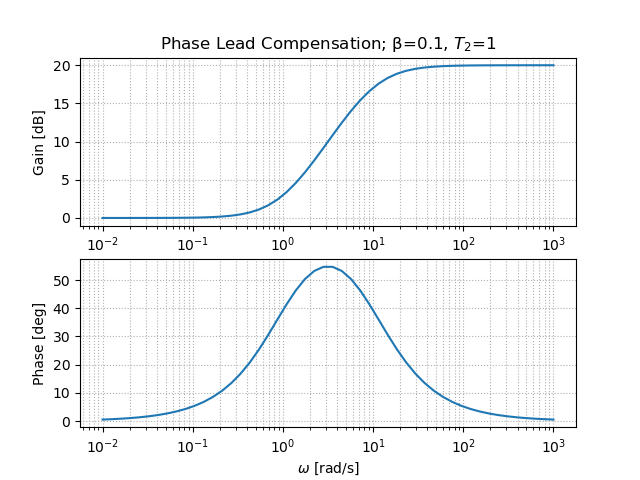
位相進み補償

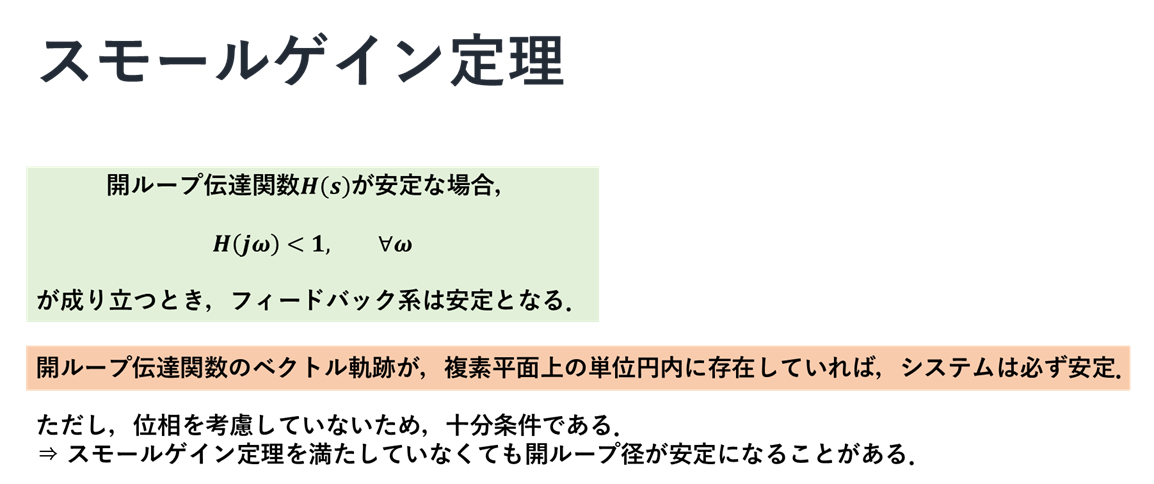
スモールゲイン定理

以下にスモールゲイン定理についてまとめる．

実装

以下に位相遅れ補償と位相進み補償についてのソースコードとそのときの出力をそれぞれ示す．

ソースコード：位相遅れ補償

phase_delay.py

"""
2021/04/03
@Yuya Shimizu

位相遅れ補償
"""
import numpy as np
import matplotlib.pyplot as plt
from control import tf, bode
from control.matlab import logspace
from for_plot import bodeplot_set


#位相遅れ補償
alpha = 10      #α
T1 = 0.1        #時定数
K1 = tf([alpha*T1, alpha], [alpha*T1, 1])       #伝達関数
gain, phase, w = bode(K1, logspace(-2, 3), Plot=False)  #ゲイン，位相，周波数

#描画
fig, ax = plt.subplots(2, 1)
ax[0].semilogx(w, 20*np.log10(gain))    #ゲイン線図
ax[1].semilogx(w, phase*180/np.pi)      #位相線図
bodeplot_set(ax)
ax[0].set_title(f"Phase Delay Compensation; α={alpha}, $T_1$={T1}")

plt.show()

出力

ソースコード：位相進み補償

phase_lead.py

"""
2021/04/03
@Yuya Shimizu

位相進み補償
"""
import numpy as np
import matplotlib.pyplot as plt
from control import tf, bode
from control.matlab import logspace
from for_plot import bodeplot_set


#位相進み補償
beta = 0.1      #β
T2 = 1        #時定数
K2 = tf([T2, 1], [beta*T2, 1])       #伝達関数
gain, phase, w = bode(K2, logspace(-2, 3), Plot=False)  #ゲイン，位相，周波数

#描画
fig, ax = plt.subplots(2, 1)
ax[0].semilogx(w, 20*np.log10(gain))    #ゲイン線図
ax[1].semilogx(w, phase*180/np.pi)      #位相線図
bodeplot_set(ax)
ax[0].set_title(f"Phase Lead Compensation; β={beta}, $T_2$={T2}")

plt.show()

出力

実践練習

以下では，実際に垂直駆動アームの制御系を設計することを題材に，位相進み遅れ補償の利用についての学習を行う．ここでの設計仕様は次のとおりである．

• ゲイン交差周波数：40 rad/s
• 位相余裕：60 deg

ソースコード

control_arm.py

"""
2021/04/03
@Yuya Shimizu

垂直駆動アームの制御系設計
（ゲイン補償・位相遅れ補償・位相進み補償）
K(s) = kK1(s)K2(s)

[設計仕様]
・ゲイン交差周波数：40 rad/s
・位相余裕：60 deg
"""
import numpy as np
import matplotlib.pyplot as plt
from control import tf, bode, feedback
from control.matlab import logspace, freqresp, margin, step
from for_plot import bodeplot_set, plot_set       #自作関数
from tf_arm import arm_tf       #自作関数

###制御対象（垂直アーム）
#パラメータ設定
g    =   9.8                    #重力加速度[m/s^2]
l     =   0.2                    #アームの長さ[m]
M   =   0.5                     #アームの質量[kg]
mu =   1.5e-2                #粘性摩擦係数[kg*m^2/s]
J    =   1.0e-2                 #慣性モーメント[kg*m^2]

#目標値
ref = 30

#制御モデル
P = arm_tf(J, mu, M, g, l)


############## 制御系設計開始 ##############

###位相遅れ補償により低周波ゲインを大きくする
#位相遅れ補償
alpha = 20      #α
T1 = 0.25        #時定数
K1 = tf([alpha*T1, alpha], [alpha*T1, 1])       #補償器

#開ループ系
H1 = P * K1

gain, phase, w = bode(H1, logspace(-1, 2), Plot=False)  #ゲイン，位相，周波数

#描画
fig, ax = plt.subplots(2, 1)
ax[0].semilogx(w, 20*np.log10(gain))    #ゲイン線図
ax[1].semilogx(w, phase*180/np.pi)      #位相線図
bodeplot_set(ax)
ax[0].set_title(f"Phase Delay Compensation; α={alpha}, $T_1$={T1}")

plt.show()

#40 radに置けるゲインと位相を確認
[[[mag]]], [[[phase]]], omega = freqresp(H1, [40])
magH1at40 = mag
phaseH1at40 = phase * (180/np.pi)
print('-'*20)
print(f"phase at 40 rad/s = {phaseH1at40}")


###位相進み補償により位相余裕が望みのものになるように位相を進ませる
#位相進み補償
phi_m = (60-(180 + phaseH1at40)) * np.pi/180
beta = (1 - np.sin(phi_m))/(1 + np.sin(phi_m))      #β
T2 = 1/40/np.sqrt(beta)        #時定数
K2 = tf([T2, 1], [beta*T2, 1])       #補償器

#開ループ系
H2 = P * K1 * K2

gain, phase, w = bode(H2, logspace(-1, 2), Plot=False)  #ゲイン，位相，周波数

#描画
fig, ax = plt.subplots(2, 1)
ax[0].semilogx(w, 20*np.log10(gain))    #ゲイン線図
ax[1].semilogx(w, phase*180/np.pi)      #位相線図
bodeplot_set(ax)
ax[0].set_title(f"PDC & PLC; α={alpha}, β={beta:.5f}, $T_1$={T1}, $T_2$={T2:.5f}")

plt.show()

#40 radに置けるゲインと位相を確認
[[[mag]]], [[[phase]]], omega = freqresp(H2, [40])
magH2at40 = mag
gainH2at40 = 20 * np.log10(magH2at40)
phaseH2at40 = phase * (180/np.pi)
print('-'*20)
print(f"gain at 40 rad/s = {gainH2at40}")
print(f"phase at 40 rad/s = {phaseH2at40}")


###ゲイン補償の設計とループ整形の結果
#ゲイン補償
k = 1/magH2at40 #H2の40 radにおけるゲインを0 dBに持っていくようにゲイン補償を設計

##開ループ系（設計後）
H = P * k * K1 * K2

gain, phase, w = bode(H, logspace(-1, 2), Plot=False)  #ゲイン，位相，周波数

#描画
fig, ax = plt.subplots(2, 1)
ax[0].semilogx(w, 20*np.log10(gain), label='H')    #ゲイン線図
ax[1].semilogx(w, phase*180/np.pi, label='H')      #位相線図
bodeplot_set(ax, 3)


##開ループ系P（設計後）
gain, phase, w = bode(P, logspace(-1, 2), Plot=False)  #ゲイン，位相，周波数

#描画
ax[0].semilogx(w, 20*np.log10(gain), ls = '--', label='P')    #ゲイン線図
ax[1].semilogx(w, phase*180/np.pi, ls = '--', label='P')      #位相線図
bodeplot_set(ax, 3)
ax[0].set_title(f"k & PDC & PLC; k={k:.5f}, α={alpha}, β={beta:.5f}, $T_1$={T1}, $T_2$={T2:.5f}")

plt.show()

# ゲイン余裕，位相余裕，位相交差周波数，ゲイン交差周波数
print('-'*20)
print('(GM, PM, wpc, wgc)')
print(margin(H))

############## 制御系設計終了 ##############

############## ループ整形前後での確認 ##############
##ステップ応答
fig, ax = plt.subplots()

#設計後の閉ループ系のステップ応答
Gyr_H = feedback(H, 1)
y, t = step(Gyr_H, np.arange(0, 2, 0.01))
ax.plot(t, y*ref, label = 'After')

#設計前の閉ループ系のステップ応答
Gyr_P = feedback(P, 1)
y, t = step(Gyr_P, np.arange(0, 2, 0.01))
ax.plot(t, y*ref, ls = '--', label = 'Before')

ax.axhline(ref, color = 'r', linewidth = 0.5)   #目標値
plot_set(ax, 't', 'y', 'best')
ax.set_title(f"Comparison Before v.s. After 'loop shaping' at closed loop")

plt.show()

##ボード線図
fig, ax = plt.subplots(2, 1)

#設計後の閉ループ系のボード線図
gain, phase, w = bode(Gyr_H, logspace(-1, 2), Plot = False)
ax[0].semilogx(w, 20*np.log10(gain), label = 'After')
ax[1].semilogx(w, phase*180/np.pi, label = 'After')

#設計前の閉ループ系のボード線図
gain, phase, w = bode(Gyr_P, logspace(-1, 2), Plot = False)
ax[0].semilogx(w, 20*np.log10(gain), ls = '--', label = 'Before')
ax[1].semilogx(w, phase*180/np.pi, ls = '--', label = 'Before')

bodeplot_set(ax, 3)
ax[0].set_title(f"Comparison Before v.s. After 'loop shaping' at closed loop")

plt.show()

出力

step1：まず，位相遅れ補償により低周波ゲインを大きくする．

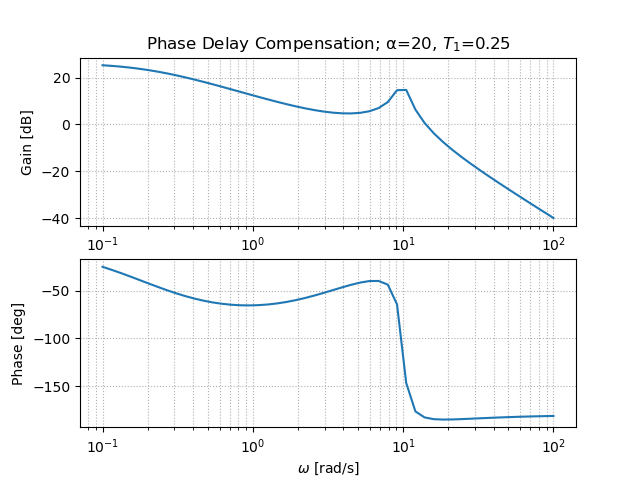
低周波ゲインが0dBから大きくなっていることが分かる．これに伴って，位相が遅れていることも確認できる．

phase at 40 rad/s = 176.86344657790153

40[rad/s]の位相交差周波数における位相は176.86...[deg]であり，位相余裕はおよそ4[deg]となり，仕様を満たさない．本当は，位相余裕を60[deg]にしたいので，60-(180-176)=56[deg]だけ位相を進ませる必要がある．

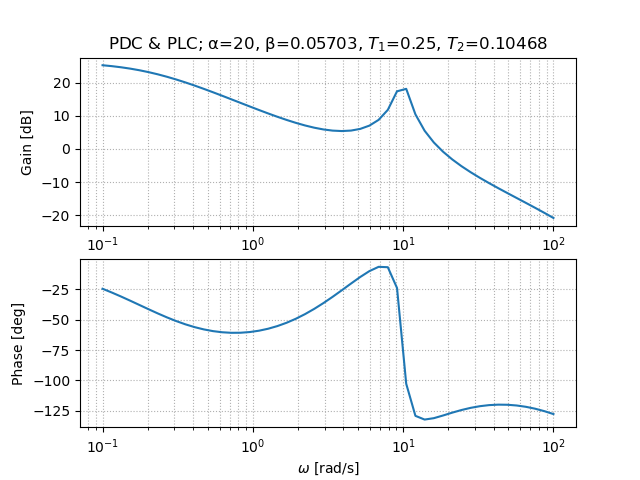
step2：位相進み補償により位相余裕が望みのものになるように位相を進ませる

位相を進ませることができていることが確認できる．

gain at 40 rad/s = -11.058587737030232
phase at 40 rad/s = -119.99999999999999

実際に位相を120[deg]にできていることが分かる．また，このときゲインがおよそ11であり，40[rad/s]のゲインを0[dB]にする．そのために，その分だけ上に移動させる．

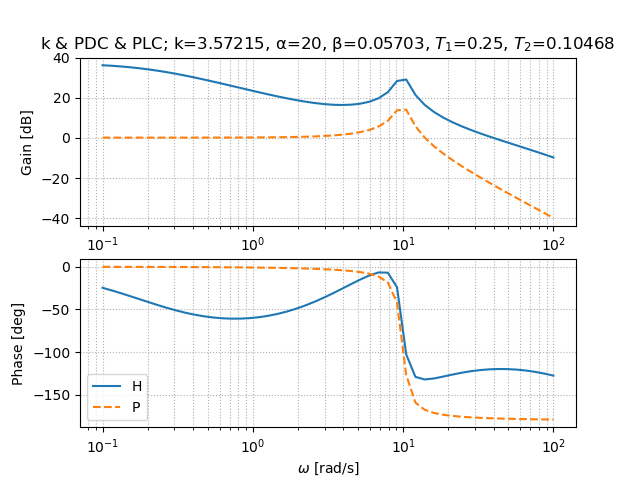
step3：ゲイン補償の設計とループ整形の結果

(GM, PM, wpc, wgc)
(inf, 60.0, nan, 40.0)

確かに，位相余裕を60[deg]に，ゲイン交差周波数を40[rad/s]にできている．
制御系設計は以上である．次にその補償器を使ったときの閉ループ系のステップ応答とボード線図を示す．

ループ整形前後での確認（ステップ応答）

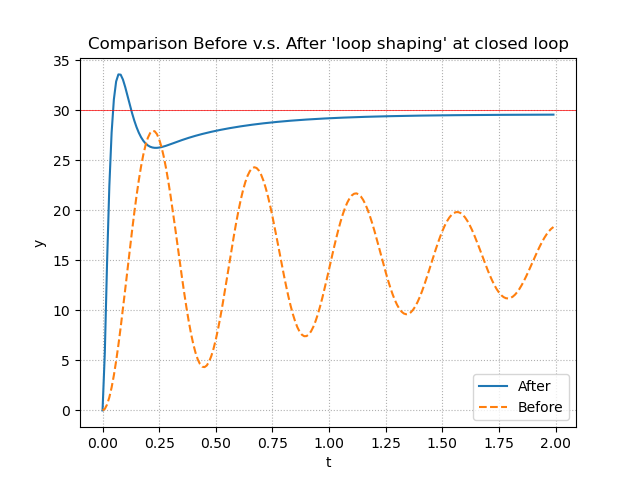
設計前にうまく目標値に収束できていなかったものが，設計後にはうまく追従できていることが分かる．

ループ整形前後での確認（ボード線図）

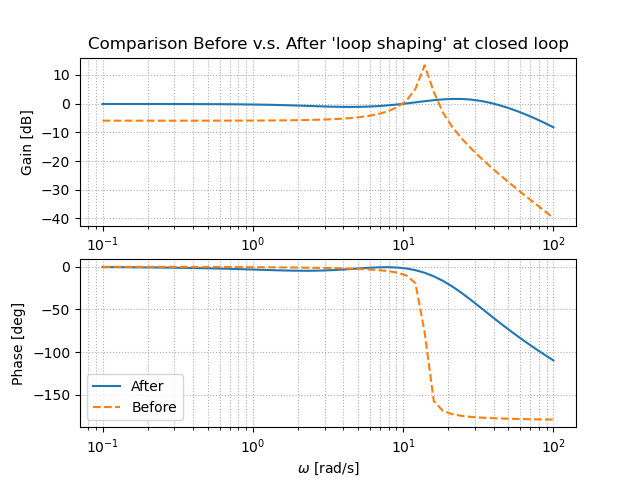
ピークゲインを抑えながら，位相余裕も確保できていることが分かる．

感想

位相進み遅れ補償は少しだけ触れたことはあったが，いまいちつかめていなかった．今回は，それらについて復習できた．PID制御との違いについても触れることができた．実際に何かを設計するときにはこのあたりの知識が役立つかもしれない．

参考文献

Pyhtonによる制御工学入門　　南 祐樹　著　　オーム社