Pythonで学ぶアルゴリズム 第20弾：並べ替え（マージソート）

#Pythonで学ぶアルゴリズム< マージソート >

はじめに

基本的なアルゴリズムをPythonで実装し，アルゴリズムの理解を深める．
その第20弾としてマージソートを扱う．

マージソート

マージソートはまず，リストを順に半分ずつにしてバラバラにする．そのイメージ図を次に示す．

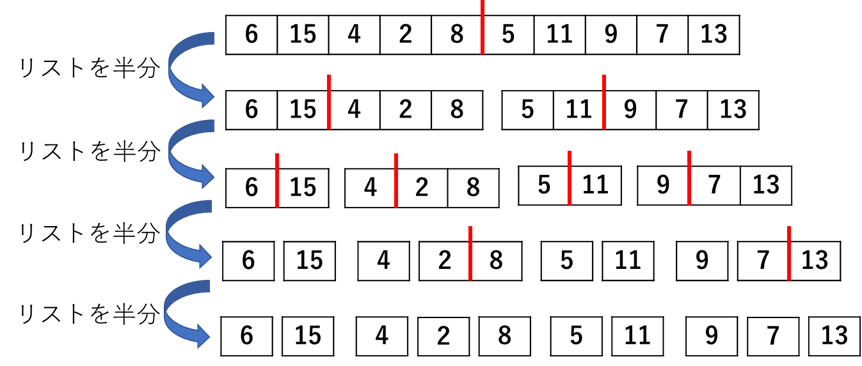
上図の最下層，つまりバラバラになったものを次は，逆に統合していく．このときに大きさを比較しながら統合していくことで，すべての要素が再構築されるときには並べ替えられた状態になっているという原理である．そのイメージ図を次に示す．

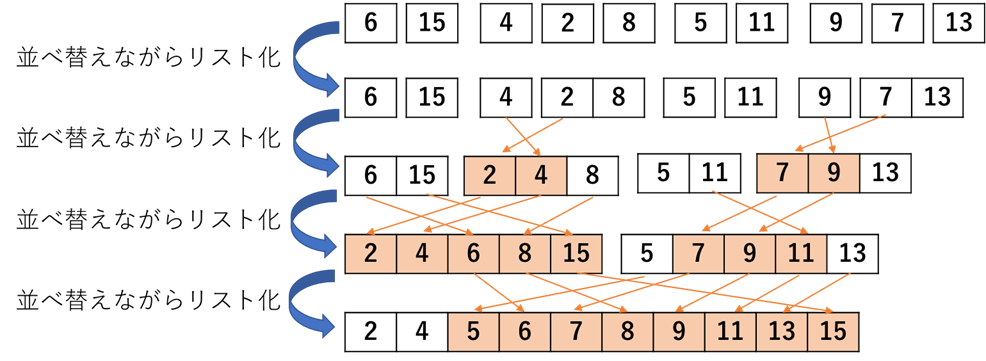
実装

再帰を使わずに実装を試みようとしたが，うまくいかなかったため，再帰を利用したコードとそのときの出力を以下に示す．

コード

merge_sort.py

"""
2021/01/22
@Yuya Shimizu

マージソート：リストを半分ずつ分割 → 並べ替えしながら再構築
"""

def merge_sort(data):
    if len(data) <= 1:
        return data

    mid = len(data) // 2    #半分の位置を計算

    # 再帰的に分割
    left = merge_sort(data[:mid])        #左側を分割
    right = merge_sort(data[mid:])      #右側を分割

    #統合
    return merge(left, right)

def merge(left, right):
    result = []
    i, j = 0, 0

    while (i < len(left)) and (j < len(right)):
        if left[i] <= right[j]:         #左<=右のとき
            result.append(left[i])    #左側から1つ取り出して追加
            i += 1
        else:
            result.append(right[j])  #右側から1つ取り出して追加
            j += 1

    # 残りをまとめて追加
    if i < len(left):
        result.extend(left[i:])      #左側の残りを追加
    if j < len(right):
        result.extend(right[j:])    #右側の残りを追加

    return result

if __name__ == '__main__':
    data = [6, 15, 4, 2, 8, 5, 11, 9, 7, 13]
    sorted_data = merge_sort(data)
    print(f"{data} → {sorted_data}")

出力

[6, 15, 4, 2, 8, 5, 11, 9, 7, 13] → [2, 4, 5, 6, 7, 8, 9, 11, 13, 15]

計算量

2つのリストを統合する処理は，できあがるリストの長さのオーダーで処理できるので，オーダー記法で表すと$O(n)$である．また統合する段数を考えると，$n$個のリストを1つになるまで統合する場合，1度の統合で2つのリストを統合することになるので，その段数は$log_2n$となる．したがって，全体の計算時間をオーダー記法で表すと$O(nlogn)$となる．

感想

今回は，再帰を使わずに何とかしようと試みたが，うまくいかなく残念であった．もう少し粘ってもよかったのだが，いまはとりあえずアルゴリズムを理解することが本筋であるため，次に進もうと思う．ただ，今回も初めて使うものがあった．extend()である．これはリストの末尾に追加するときに使う．+と似ているが，文字列を追加するときに使うと，1文字ずつ追加してしまうようだ．append()と+ぐらいしかリストには使ってきていなかったため，良い学びとなった．次回はクイックソートである．

参考文献

Pythonで始めるアルゴリズム入門　伝統的なアルゴリズムで学ぶ定石と計算量
　　　　　　　　　　　　　　　　　　　　　　　　 増井 敏克　著　　翔泳社