#Pythonで学ぶアルゴリズム< Boyer-Moore法 >
はじめに
基本的なアルゴリズムをPythonで実装し,アルゴリズムの理解を深める.
その第28弾としてBoyer-Moore法を扱う.
Boyer-Moore法
力任せ法では,不一致になった場合に1文字ずつずらしてパターンの探索を実行していた.しかし,いい感じに大きくずらすことができれば高速化ができそうなことは容易に想像できる.これを実現するのが,Boyer-Moore法である.文字列探索を効率的に行うアルゴリズムとして,KMP法やBoyer-Moore法があるが,KMP法は理論上は高速であるものの実用上はそれほど高速に処理できないらしいので,Boyer-Moore法をここでは扱う.
Boyer-Moore法はパターンの末尾から比較することで処理を高速化する.その処理の流れについてのイメージ図を次に示す.

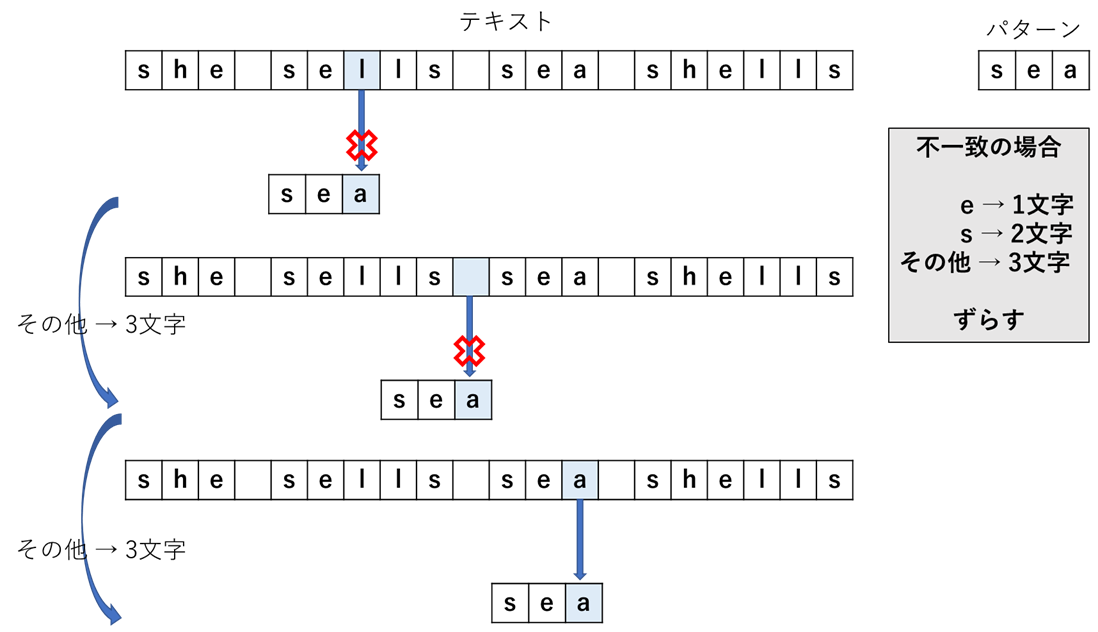

たったこれだけの手順でパターンの発見ができた.はじめにも記述したとおり,いい感じにずらすとは無駄のないずらし方であり,上図にもあるように,不一致な場合にパターンの中にある文字であるならそれと重なるようにずらしてやり,パターンの中になければ,パターンの文字数だけずらせばよい.
実装
先ほどの説明に従って,Pythonでの実装を行う.以下にソースコードとそのときの出力を示す.
ソースコード
"""
2021/02/02
@Yuya Shimizu
Boyer-Moore法
"""
def boyer_moore(text, pattern):
skip = {}
#パターンの文字に応じたずらしを記録
for i in range(len(pattern) - 1):
skip[pattern[i]] = len(pattern) - i -1
i = len(pattern) - 1 #探索初期値はテキストとパターンの先頭が合うようにしたときの末尾になるように設定
while i < len(text):
match = True #patternと一致すると仮定
for j in range(len(pattern)):
#patternを順に1文字ずつ比較する
if text[i - j] != pattern[-1-j]:
match = False #不一致
break #探索箇所を次に移行するため,これ以上の探索はしない
if match: #すべて一致した ⇒ 発見 ⇒ 探索終了
return i - len(pattern) + 1 #末尾から探索しているため先頭の位置を返す処理を行う
if text[i] in skip:
i += skip[text[i]] #先ほどの結果から得られた探索箇所をずらす分を足し合わせる
else:
i += len(pattern) #ずらす対象がとくに見当たらなければ,パターンの文字数だけずらす
if __name__ == '__main__':
TEXT = 'she sells sea shells'
PATTERN = 'shells'
where = boyer_moore(TEXT, PATTERN)
if where is not None:
print(f"{where}\nthat is, you can find '{PATTERN}' by running 'TEXT[{where}: {where}+len(PATTERN)]'")
else:
print(f"Failure\nthat is, you can't find '{PATTERN}' in the TEXT")
出力
14
that is, you can find 'shells' by running 'TEXT[14: 14+len(PATTERN)]'
探索はパターンの末尾からだが,出力は前回の力任せ法同様に,テキストの先頭からどのくらいの位置にあるのかということである.ソースコードにおいてもその変換処理が施されていることが分かる.
力任せ法との比較
表1に示すのは,3つの例において,処理を行いそれぞれ末尾にある25文字ほどの文字列を探したときの力任せ法とBoyer-Moore法での処理時間の比較結果をまとめたものである.
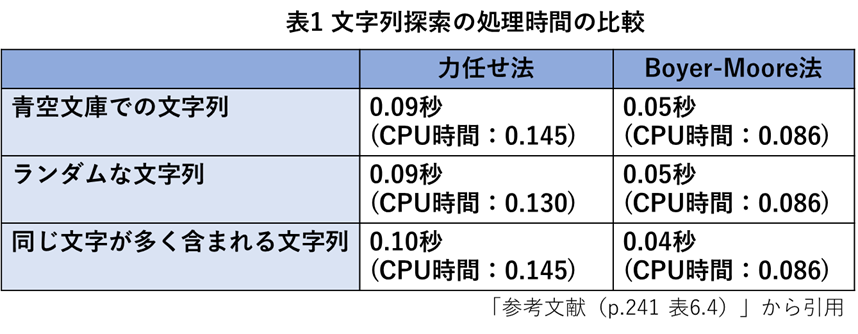
ここで,例について補足しておく.
・青空文庫での文字列:
青空文庫から太宰治の「人間失格」を使う.7万文字を超える文章.
・ランダムな文字列:
「あ」から「ん」までの文字をランダムに約7万文字並べて作成した文章.
・同じ文字が多く含まれる文字列:
「ABCDEFGHIJKLMNOPQRSTUVWXYZ」という文字列を繰り返し,約7万文字になるように作成した文章.
表1の結果から,文字列の内容の違いによる処理時間の違いというのはそれほどないことが分かる.これは25文字程度では,途中まで一致していた状態で不一致となってやり直す影響がそれほど大きくないことが考えられる.また,現代のコンピュータにおいては,7万文字程度のテキストであれば,力任せ法でも一瞬で処理できてしまう.膨大なデータから何度も繰り返し検索するような場合には,Boyer-Moore法が有効な場面もあるが,目的に応じて使い分けるとよいらしい.
感想
実際にBoyer-Moore法の原理を図示してみて確かに力任せ法よりも高速にできそうだと納得できた.しかしながら,現代のコンピュータ処理能力においては,力任せ法でもそこそこのものを処理してしまうということで,コンピュータの著しい発展に驚きながらもありがたいと思う.
参考文献
Pythonで始めるアルゴリズム入門 伝統的なアルゴリズムで学ぶ定石と計算量
増井 敏克 著 翔泳社