#Pythonで学ぶアルゴリズム< 逆ポーランド記法 >
はじめに
基本的なアルゴリズムをPythonで実装し,アルゴリズムの理解を深める.
その第29弾として逆ポーランド記法を扱う.
演算の記法
まず,演算の記法を3つ示す.1つは人間の世界でよく見る記法で,他の2つはコンピュータが処理しやすい形にしたものである.その3つの記法の概要および例を以下に示す.



演算の記法②と③はよく似ていることが分かる.ここで,演算の記法②ポーランド記法の木構造を次に示し,構造の理解を深める.
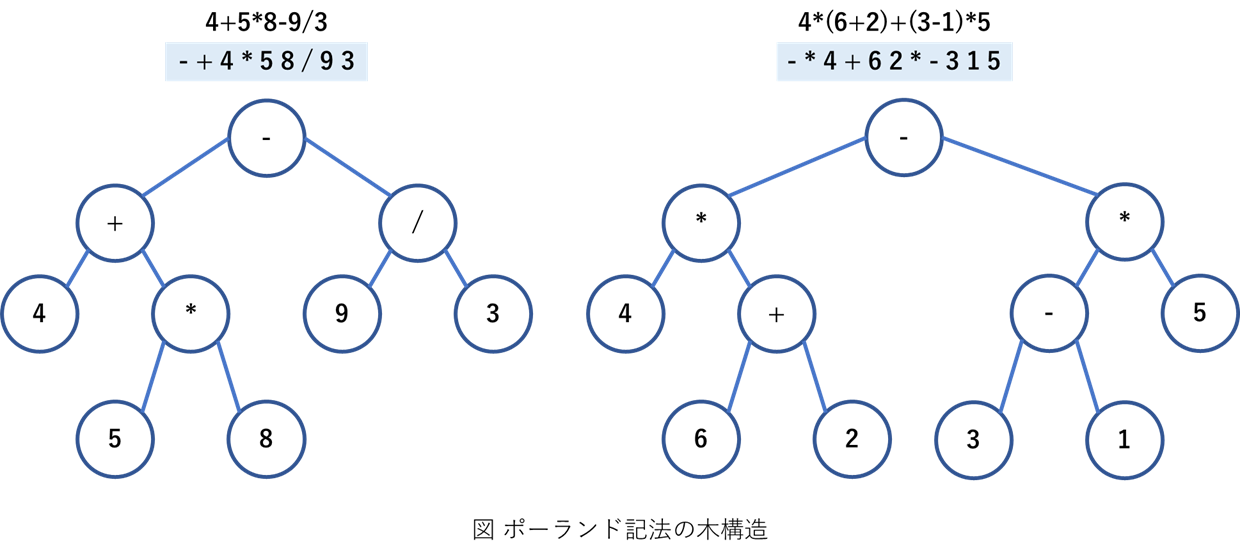
2つ子ノードを1つの親ノードにある演算子で処理を行うといった形でとらえられる.上の概要図で示していたとおり,スタックを使って処理しやすいのは逆ポーランド記法であるので,今回は逆ポーランド記法についてより詳しく見ていくこととする.実際にスタックを適用したときのイメージ図を次に示す.
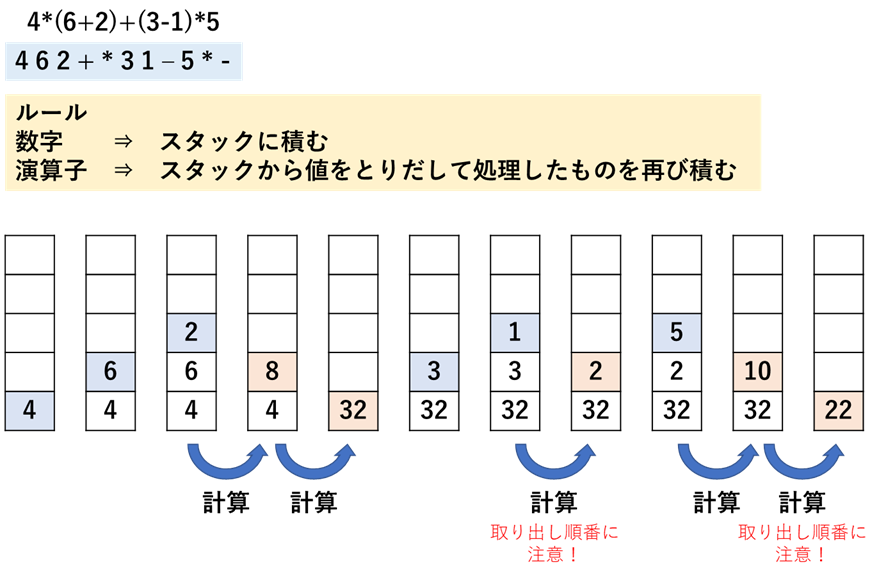
上図のスタックにおいて,青色で塗りつぶされているのが,処理する文字列の先頭から積み上げたものであり,桃色で塗りつぶされているのが,処理する文字列の先頭から積み上げた演算子を使って,今スタックにある上から2つの数値を計算した結果を積み上げたものである.なお,計算順に注意というのは,特に減算と除算である.[取り出し①] -(or /) [取り出し②] このようになる.
実装
先ほどの説明に従って,逆ポーランド記法で記述された処理の演算をPythonで実装する.以下にソースコードとそのときの出力を示す.なお,ソースコードは2つ作成した.1つ目は参考文献にも載っているとおりのもので,処理内容が見やすいものとなっている.2つ目は一部をまとめて記述することで,ソースコードの長さを短くしている.
ソースコード①
"""
2021/02/03
@Yuya Shimizu
逆ポーランド記法
"""
def calc(expression):
stack = []
for i in expression.split(' '):
if i == '+':
# +のときはスタックから2つ取り出して加算し,再度格納する
b, a = stack.pop(), stack.pop() #後の演算のために順序を整えている
stack.append(a + b)
elif i == '-':
# -のときはスタックから2つ取り出して減算し,再度格納する
b, a = stack.pop(), stack.pop() #後の演算のために順序を整えている
stack.append(a - b)
elif i == '*':
# *のときはスタックから2つ取り出して乗算し,再度格納する
b, a = stack.pop(), stack.pop() #後の演算のために順序を整えている
stack.append(a * b)
elif i == '/':
# /のときはスタックから2つ取り出して除算し,再度格納する
b, a = stack.pop(), stack.pop() #後の演算のために順序を整えている
stack.append(a / b)
else:
stack.append(int(i)) #受け取っているものは文字列であるが,後に計算されるので,intに変換
return stack.pop()
if __name__ == '__main__':
expression = '4 6 2 + * 3 1 - 5 * -' #逆ポーランド記法で記述
result = calc(expression)
print(f"{expression} → {result}")
出力
4 6 2 + * 3 1 - 5 * - → 22
ソースコード②(短縮化)
"""
2021/02/03
@Yuya Shimizu
逆ポーランド記法(プログラムの短縮化)
"""
def calc(expression):
stack = []
operator = ['+', '-', '*', '/'] #演算子
for i in expression.split(' '):
if i in operator:
# 演算子であるときはスタックから2つ取り出してその演算子に従い計算し,再度格納する
b, a = stack.pop(), stack.pop() #後の演算のために順序を整えている
result = eval(f"{a} {i} {b}")
stack.append(result)
else:
stack.append(int(i)) #受け取っているものは文字列であるが,後に計算されるので,intに変換
return stack.pop()
if __name__ == '__main__':
expression = '4 6 2 + * 3 1 - 5 * -' #逆ポーランド記法で記述
result = calc(expression)
print(f"{expression} → {result}")
出力
4 6 2 + * 3 1 - 5 * - → 22
この短縮化の結果,ソースコード②はソースコード①に比べて,13行短いコードとなった.
感想
今回は記法を変えるだけで,スタックのように別のアルゴリズムが使えるようになることを知った.また,構造が単純だったゆえにeval()を使うことで,プログラムの短縮化をすることもできた.残るアルゴリズムは「ユークリッドの互除法」と「圧縮アルゴリズム」となった.
参考文献
Pythonで始めるアルゴリズム入門 伝統的なアルゴリズムで学ぶ定石と計算量
増井 敏克 著 翔泳社