#Pythonで学ぶ制御工学< ロバスト制御 >
はじめに
基本的な制御工学をPythonで実装し，復習も兼ねて制御工学への理解をより深めることが目的である．
その第24弾として「ロバスト制御」を扱う．
概要
ロバスト制御
以下にロバスト制御についてまとめたものを示す．
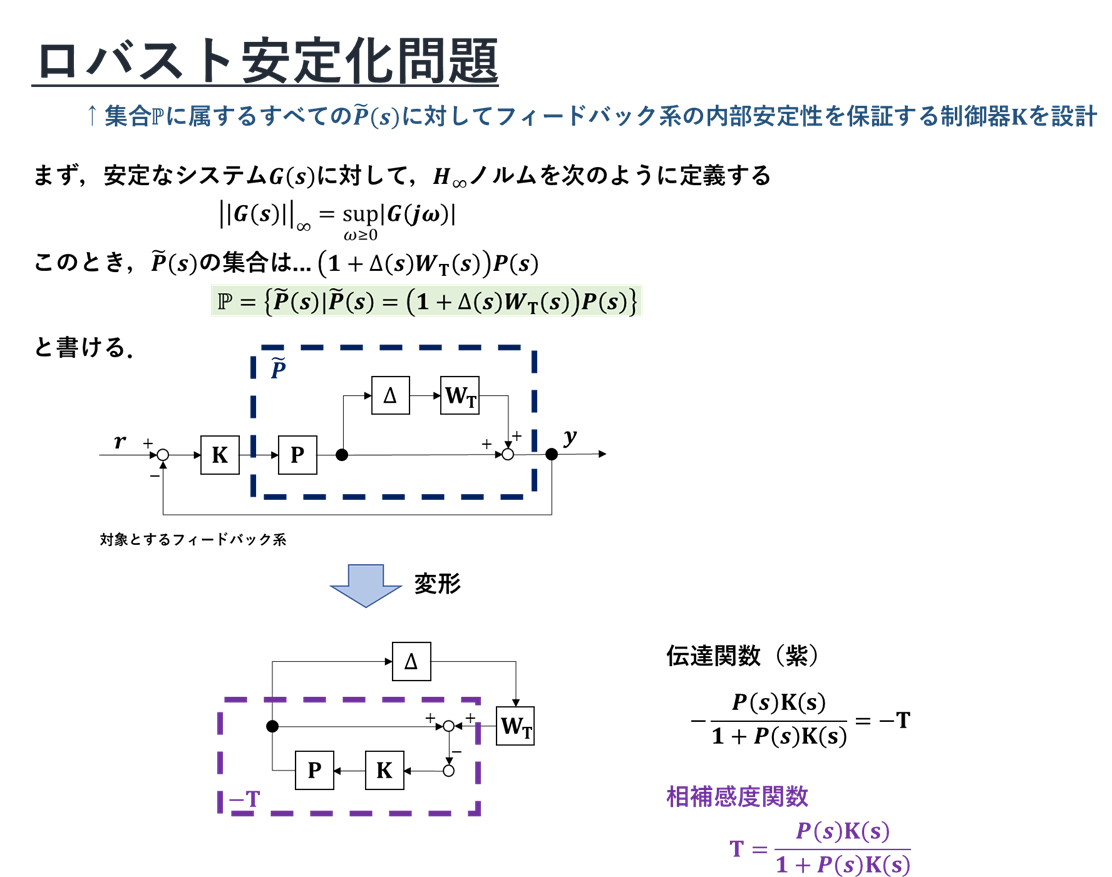
ロバスト安定化問題
次にロバスト安定化についてもまとめておく．
実装
垂直駆動アームの角度制御を例に不確かさを有する制御対象とロバスト制御器の設計について実装する．以下にソースコードとそのときの出力をそれぞれ示す．
ソースコード：不確かさを有する制御対象
uncertainty.py
"""
2021/04/10
@Yuya Shimizu
乗法的不確かさを有する制御対象
"""
import numpy as np
import matplotlib.pyplot as plt
from control import bode, tf
from control.matlab import logspace
from tf_arm import arm_tf
from for_plot import bodeplot_set
###垂直アームのノミナルモデル
g = 9.81 #重力加速度 [m/s^2]
l = 0.2 #アームの長さ[m]
M = 0.5 #アームの質量[kg]
mu = 1.5e-2 #粘性摩擦係数[kg*m^2/s]
J = 1.0e-2 #慣性モーメント[kg*m^2]
Pn = arm_tf(J, mu, M, g, l)
###不確かさ
delta = np.arange(-1, 1, 0.1)
WT = tf([10, 0], [1, 150])
fig, ax = plt.subplots(1, 2)
for i in range(len(delta)):
#不確かさをもつ制御対象
P = (1 + WT*delta[i])*Pn
gain, _, w = bode(P, logspace(-3, 3), Plot = False)
ax[0].semilogx(w, 20*np.log10(gain), color='k', lw=0.3)
#乗法的不確かさ
DT = (P - Pn)/Pn
gain, _, w = bode(DT, logspace(-3, 3), Plot = False)
ax[1].semilogx(w, 20*np.log10(gain), color='k', lw=0.3)
gain, _, w = bode(Pn, logspace(-3, 3), Plot = False)
ax[0].semilogx(w, 20*np.log10(gain), color='k', lw=2)
gain, _, w = bode(WT, logspace(-3, 3), Plot = False)
ax[1].semilogx(w, 20*np.log10(gain), color='k', lw=2)
bodeplot_set(ax)
ax[0].set_xlabel('$\omega$ [rad/s]')
ax[0].set_ylabel('Gain of $P$ [dB]')
ax[1].set_xlabel('$\omega$ [rad/s]')
ax[1].set_ylabel('Gain of $\Delta W_T/P$ [dB]')
fig.suptitle("Gain of control target with Certainty")
plt.show()
出力
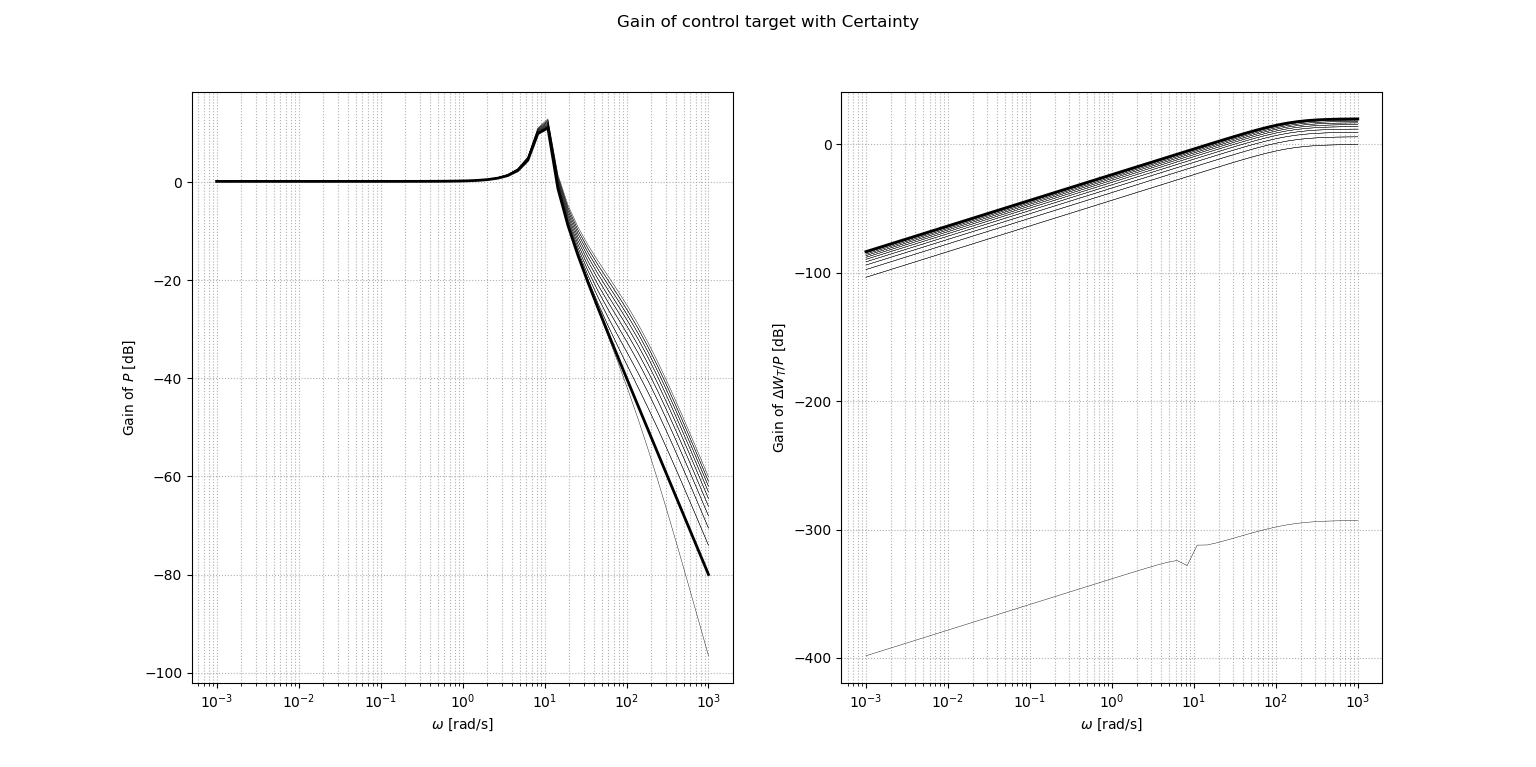
図の左が不確かさをもつ制御対象を，右がその不確かさをプロットしたものである．なお，太線のグラフは不確かさをもたないノミナルモデルである．高周波域でゲインがバラついていることが分かる．これは，入力信号の高周波成分に対する応答がバラつくことを意味する．例えば，速応性をよくするために制御器のゲインを大きくしたときに，望ましい応答が得られない（不安定化する）可能性がある．
ソースコード：ロバスト制御器の設計
robust.py
"""
2021/04/10
@Yuya Shimizu
ロバスト制御器の設計
"""
import numpy as np
import matplotlib.pyplot as plt
from control import bode, tf, mixsyn, ss2tf
from control.matlab import logspace, feedback, step
from tf_arm import arm_tf
from for_plot import plot_set
###垂直アームのノミナルモデル
g = 9.81 #重力加速度 [m/s^2]
l = 0.2 #アームの長さ[m]
M = 0.5 #アームの質量[kg]
mu = 1.5e-2 #粘性摩擦係数[kg*m^2/s]
J = 1.0e-2 #慣性モーメント[kg*m^2]
Pn = arm_tf(J, mu, M, g, l)
###重み関数の定義
WS = tf([0, 1], [1, 1, 0.25]) #感度関数に対する重み関数
WU = tf(1, 1)
WT = tf([10, 0], [1, 150]) #相補感度関数に対する重み関数
###混合感度問題
K, _, gamma = mixsyn(Pn, w1 = WS, w2 = WU, w3 = WT) #混合感度問題を解く
print('K=', ss2tf(K))
print('gamma=', gamma[0])
fig, ax = plt.subplots(1, 2)
###感度関数
Ssys = feedback(1, Pn*K)
gain, _, w = bode(Ssys, logspace(-3, 3), Plot = False)
ax[0].semilogx(w, 20*np.log10(gain), lw=2, label='$S$')
gain, _, w = bode(1/WS, logspace(-3, 3), Plot = False)
ax[0].semilogx(w, 20*np.log10(gain), ls='-.', label='$1/W_S$')
###相補感度関数
Tsys = feedback(Pn*K, 1)
gain, _, w = bode(Tsys, logspace(-3, 3), Plot = False)
ax[1].semilogx(w, 20*np.log10(gain), lw=2, label='$T$')
gain, _, w = bode(1/WT, logspace(-3, 3), Plot = False)
ax[1].semilogx(w, 20*np.log10(gain), ls='--', label='$1/W_T$')
for i in range(2):
ax[i].set_ylim(-40, 40)
ax[i].legend()
ax[i].grid(which="both", ls=':')
ax[i].set_ylabel('Gain [dB]')
ax[i].set_xlabel('$\omega$ [rad/s]')
fig.tight_layout()
fig.suptitle("robust controller")
plt.show()
###設計した制御器の性能確認
fig, ax = plt.subplots()
ref = 30 #目標値30
#不確かさ
delta = np.arange(-1, 1, 0.1)
WT = tf([10, 0], [1, 150])
#不確かさを有するモデルに対する性能
for i in range(len(delta)):
#不確かさをもつ制御対象
P = (1 + WT*delta[i])*Pn
Gyr = feedback(P*K, 1)
y, t = step(Gyr, np.arange(0, 5, 0.01))
ax.plot(t, y*ref, color='k', lw=0.3)
#ノミナルモデル（不確かさなし）に対する性能
Gyr = feedback(Pn*K, 1)
y, t = step(Gyr, np.arange(0, 5, 0.01))
ax.plot(t, y*ref, color='r', lw=2, label="nominal model")
ax.legend()
plot_set(ax, 't', 'y')
ax.set_title("robust controller test in model")
plt.show()
出力
K=
7.21 s^4 + 1098 s^3 + 3259 s^2 + 1.081e+05 s + 9.032e+04
---------------------------------------------------------------
s^5 + 165.1 s^4 + 2448 s^3 + 2.449e+04 s^2 + 2.273e+04 s + 5540
gamma= 0.9527651218302327
上の計算結果から，混合感度問題を解くと，5次の制御器$K(s)$が得られることが分かる．また，$\gamma$は1より小さい値であることも確認できる．
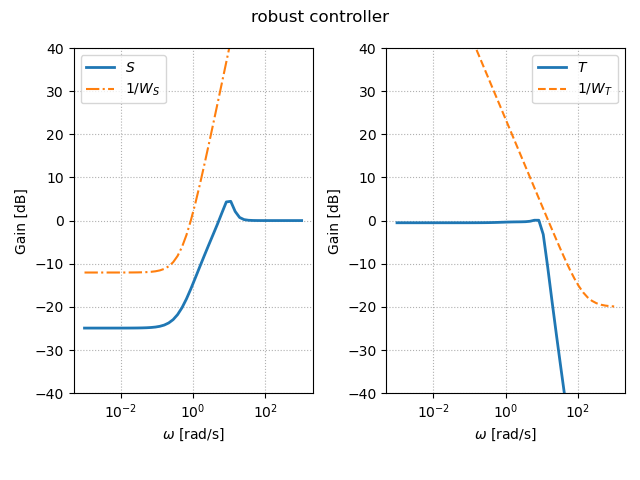
上図は，感度関数と相補感度関数のゲイン線図である．それぞれ重み関数の逆数のゲイン線図よりも下側に描かれていることが確認できる．
以上により，設計された制御器を用いたときのステップ応答を次に示す．
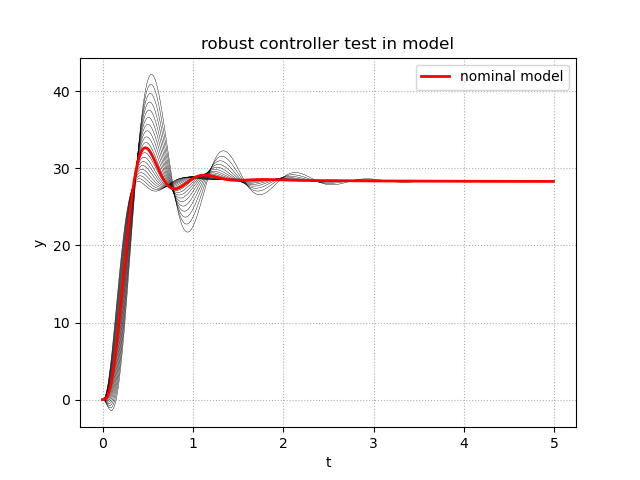
図において，赤線は不確かさをもたない元の制御対象ノミナルモデルであり，それ以外が不確かさをもつ制御対象である．速やかに目標に追従していることと，不確かさがあっても応答があまり変わっていないことが分かる．
感想
ロバスト制御についての概要を把握することはできた．しかしながら，これをどのようにうまく利用してくのかという部分についてはまだまだ経験・知識不足であると感じた．概要はつかめたため，何かしらの教材か論文などでそのあたりの知識を埋めていきたいと思う．
参考文献
Pyhtonによる制御工学入門 南 祐樹 著 オーム社