Pythonで学ぶ制御工学 第13弾：周波数応答

#Pythonで学ぶ制御工学< 周波数応答 >

##はじめに
基本的な制御工学をPythonで実装し，復習も兼ねて制御工学への理解をより深めることが目的である．
その第13弾として「周波数応答」を扱う．

##周波数応答
周波数応答の概要についてから，以下の図に説明を示す．

ここで，実際に図を示す．（※ソースコードは後に示す）

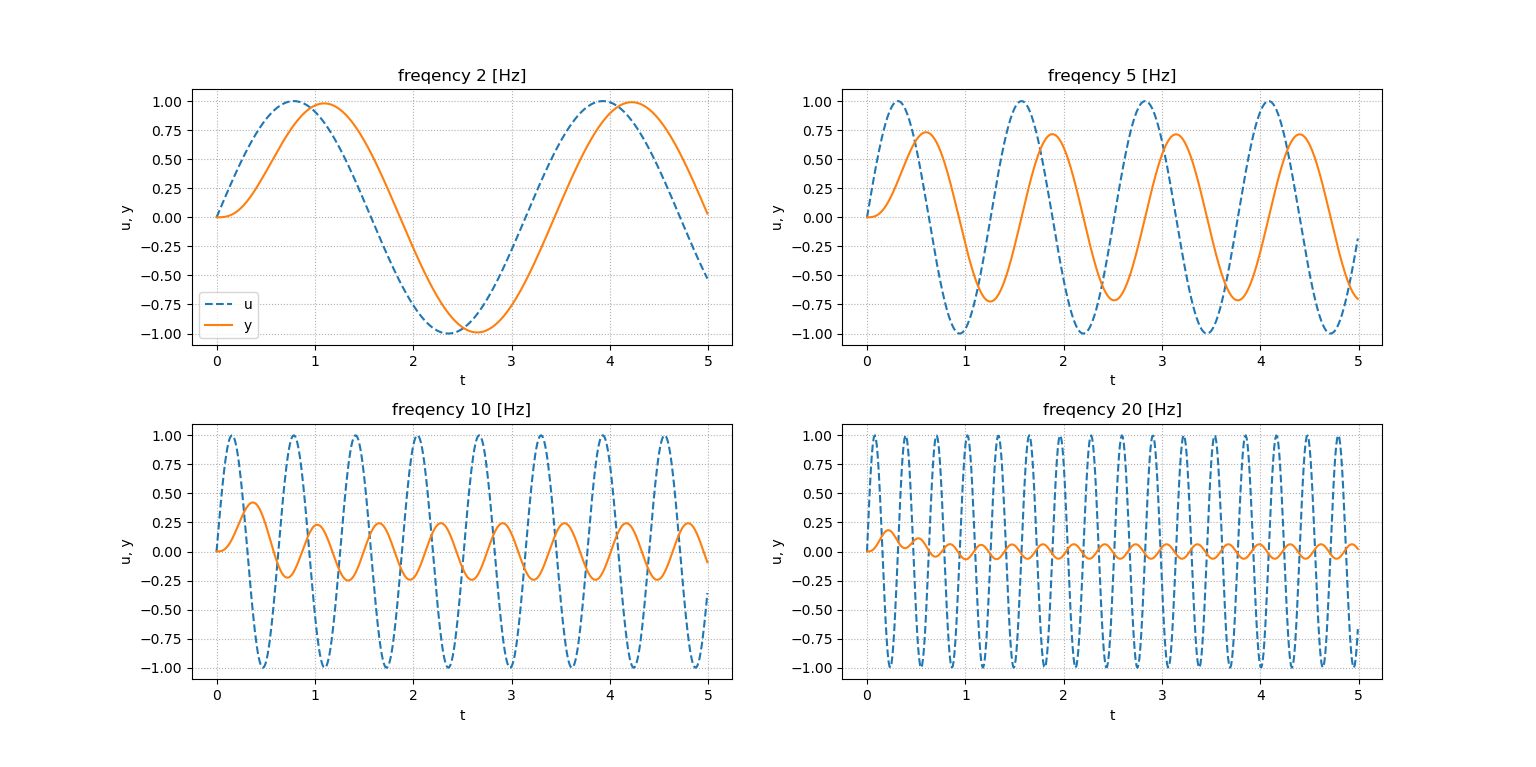
確かに位相はずれており，周波数を高くするほど出力信号の振幅が小さくなっていることが分かる．

ここまでをまとめると，次のような感じである．
「制御対象の特徴を知るためにインパルス入力によるインパルス応答を観測すればよいが，インパルス入力は難しいため，代わりに複数の周波数の余弦波（正弦波）の集まり，すなわち様々な周波数成分を含んだ信号を入力として，周波数に対する応答（周波数応答）を観測すればよいということに置き換えられる．そこで，ゲインや位相という話が出てくる．」

##1次遅れ系
1次遅れ系での周波数応答について，以下の図にて簡単な説明を示す．

ここで，時定数$T$を変化させたときの1次遅れ系のボード線図を示す．（※ソースコードは後に示す）

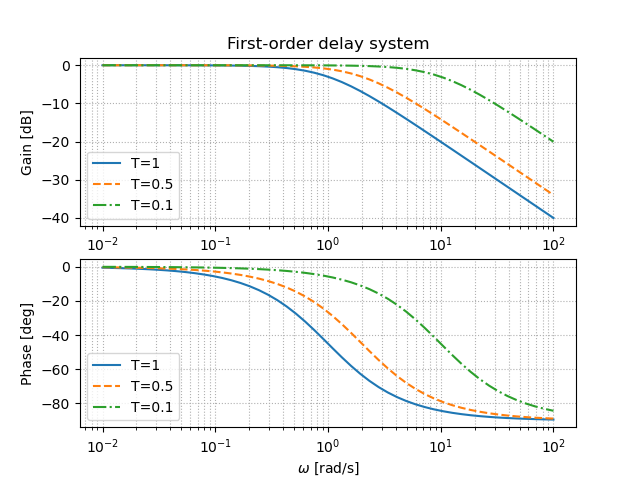
確かに周波数が時定数の逆数となる時に位相が-45度付近にあり，そのときの周波数あたりでゲイン線図では，およそ-3dBにあることが分かる．

##2次遅れ系
2次遅れ系での周波数応答について，以下の図にて簡単な説明を示す．

ここで，減衰係数$\zeta$を変化させたときの2次遅れ系のボード線図と，固有角振動数$\omega_n$を変化させたときの2次遅れ系のボード線図を示す．（※ソースコードは後に示す）


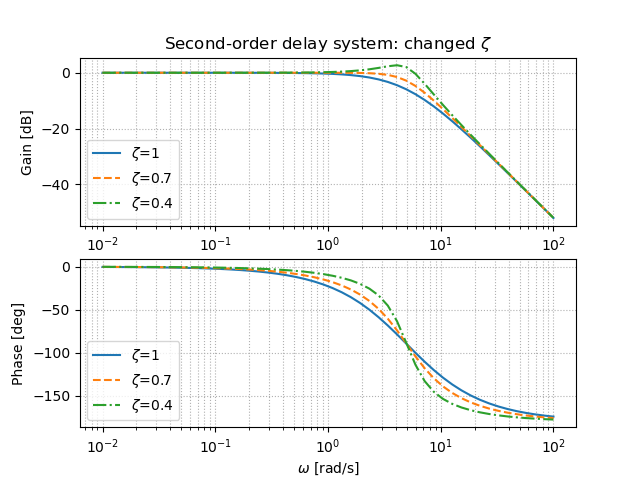
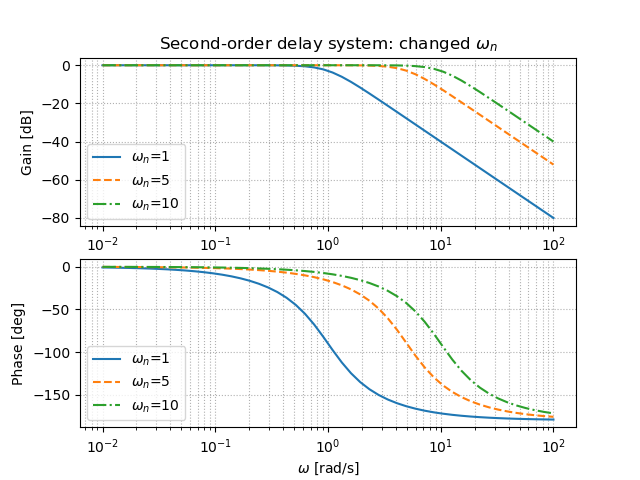
確かに減衰係数$\zeta$が0.4と小さい時にゲインが0を上回っている．また，固有角振動数$\omega_n$と周波数が一致するところで，位相が-90度付近にあり，そのときの周波数あたりで，ゲインが下がり始めていることが確認できる．

##実装
上で示した図を生成したソースコードを以下に示す．
#####ソースコード①：周波数の違いによる応答

frequency.py

"""
2021/03/07
@Yuya Shimizu

正弦波を入力したときの応答を調べる
"""
from control import tf
from control.matlab import lsim
import matplotlib.pyplot as plt 
import numpy as np
from for_plot import plot_set       #自分で定義した関数をインポート
#定義した関数について (https://qiita.com/Yuya-Shimizu/items/f811317d733ee3f45623)

fig, ax = plt.subplots(2, 2)

#2次遅れ系
zeta = 0.7
omega_n = 5
K = 1
P = tf([0, K*omega_n**2], [1, 2*zeta*omega_n, omega_n**2])

freq = [2, 5, 10, 20]   #周波数を4つ用意
Td = np.arange(0, 5, 0.01)  #シミュレーション時間

for i in range(2):
    for j in range(2):
        u = np.sin(freq[i+j+i*1]*Td)    #正弦波入力
        y, t, x0 = lsim(P, u, Td, 0)    #シミュレーション

        #描画
        ax[i, j].plot(t, u, ls='--', label='u')
        ax[i, j].plot(t, y, label='y')
        ax[i, j].set_title(f"freqency {freq[i+j+i*1]} [Hz]")
        plot_set(ax[i, j], 't', 'u, y')

ax[0, 0].legend()   #1つ目の図だけ凡例表示

plt.show()

#####ソースコード②：ボード線図（1次遅れ系）

bode1.py

"""
2021/03/07
@Yuya Shimizu

ボード線図（1次遅れ系）
"""
from control import tf, bode
from control.matlab import lsim, logspace
import matplotlib.pyplot as plt
import numpy as np
from for_plot import linestyle_generator, bodeplot_set      #自分で定義した関数をインポート
#定義した関数について (https://qiita.com/Yuya-Shimizu/items/f811317d733ee3f45623)

K = 1
T = [1, 0.5, 0.1]   #時定数

LS = linestyle_generator()
fig, ax = plt.subplots(2, 1)

for i in range(len(T)):
    P = tf([0, K], [T[i], 1])   #1次遅れ系

    #ゲイン，位相，周波数の取得　※Plot=Falseとすることで，値だけ取得し図は出力しない
    gain, phase, w = bode(P, logspace(-2, 2), Plot=False)

    #ボード線図をプロット
    plt_args = {'ls':next(LS), 'label': f"T={T[i]}"}
    ax[0].semilogx(w, 20*np.log10(gain), **plt_args)    #.semilogxでx軸に対数表現を置いた片側対数グラフにプロット
    ax[1].semilogx(w, phase*180/np.pi, **plt_args)      #度数表現

ax[0].set_title("First-order delay system")
bodeplot_set(ax, 3, 3)
plt.show()

#####ソースコード③：ボード線図（2次遅れ系）

bode2.py

"""
2021/03/07
@Yuya Shimizu

ボード線図（2次遅れ系）
"""
from control import tf, bode
from control.matlab import lsim, logspace
import matplotlib.pyplot as plt
import numpy as np
from for_plot import linestyle_generator, bodeplot_set     #自分で定義した関数をインポート
#定義した関数について (https://qiita.com/Yuya-Shimizu/items/f811317d733ee3f45623)


##減衰係数の変化によるボード線図の違い
K = 1
zeta = [1, 0.7, 0.4]   #減衰係数
omega_n = 5

LS = linestyle_generator()
fig, ax = plt.subplots(2, 1)

for i in range(len(zeta)):
    P = tf([0, K*omega_n**2], [1, 2*zeta[i]*omega_n, omega_n**2])   #2次遅れ系

    #ゲイン，位相，周波数の取得　※Plot=Falseとすることで，値だけ取得し図は出力しない
    gain, phase, w = bode(P, logspace(-2, 2), Plot=False)

    #ボード線図をプロット
    plt_args = {'ls':next(LS), 'label': f"$\zeta$={zeta[i]}"}
    ax[0].semilogx(w, 20*np.log10(gain), **plt_args)    #.semilogxでx軸に対数表現を置いた片側対数グラフにプロット
    ax[1].semilogx(w, phase*180/np.pi, **plt_args)      #度数表現

ax[0].set_title("Second-order delay system: changed $\zeta$")
bodeplot_set(ax, 3, 3)
plt.show()


##固有角振動数の変化によるボード線図の違い
K = 1
zeta = 0.7
omega_n = [1, 5, 10]    #固有角振動数

LS = linestyle_generator()
fig, ax = plt.subplots(2, 1)

for i in range(len(omega_n)):
    P = tf([0, K*omega_n[i]**2], [1, 2*zeta*omega_n[i], omega_n[i]**2])   #2次遅れ系

    #ゲイン，位相，周波数の取得　※Plot=Falseとすることで，値だけ取得し図は出力しない
    gain, phase, w = bode(P, logspace(-2, 2), Plot=False)

    #ボード線図をプロット
    plt_args = {'ls':next(LS), 'label': f"$\omega_n$={omega_n[i]}"}
    ax[0].semilogx(w, 20*np.log10(gain), **plt_args)    #.semilogxでx軸に対数表現を置いた片側対数グラフにプロット
    ax[1].semilogx(w, phase*180/np.pi, **plt_args)      #度数表現

ax[0].set_title("Second-order delay system: changed $\omega_n$")
bodeplot_set(ax, 3, 3)
plt.show()

##感想
改めて，図だけでなく式にも触れて周波数応答について学び，-3dBや-45 degとなるときの条件がなぜそうなのかなど，理論的に理解することができた．それを知ったうえで図を見るとボード線図は非常に役立つ図だと感じられる．この理論から知るか知らないかでは大きな差があるだろうと思った．自分自身も完ぺきではないが，これからもより理解を深められるように努めたい．

##参考文献
Pyhtonによる制御工学入門　　南 祐樹　著　　オーム社